进制的计算方法

目录

一、什么是进制

二、进制是干什么的

三、进制的计数规则

四、进制相互转换

五、用计算器计算进制

六、进制前缀

---

一、什么是进制

生活中进制无处不在，最常用的就是十进制。如果你没有接触过计算机或者是通信相关的知识，那么大概率你只知道十进制的计算方法。在遇到其他进制时会感觉很奇怪，比如十进制的1 + 1 = 2，但是二进制的1 + 1 = 10。注意这里的二进制1 + 1 = 10，里面的10不是读作“十”，而应该读作“一零”。如果你是读作“十”，则你不理解进制运算的原因找到了，你没弄清楚进制是干什么的。

二、进制是干什么的

进制的作用就是用来计数的

以十进制为例，十进制的含义是用一组0 ~ 9的数字来表示数量，如5个苹果。那如果苹果的数量超过9怎么办呢？此时就需要用这0 ~ 9的数字组合来表示，如12个苹果。说到十进制，相信都能够理解。其实生活中大部分用到的都是十进制，或者是用十进制简化的。

例如钟表的进制为六十进制，即0 ~ 59的数字。但是你为什么会很容易理解六十进制呢？因为其实这也是十进制，可以看成是十进制的0 - 59 - 0的循环。生活中很多的进制都简化了，刚才的钟表例子，以及我们可以想到的，如周的概念（七进制），也是简化的十进制的0 - 6 - 0的循环。这也是为什么在美国每周的第一天是周日，因为周日代表0，一周的时间从0开始。当然这么解释是不合理的，还要考虑到他们的文化背景，只是从0开始听起来挺合理的。

只要是0 - n - 0的计数模式，都是用十进制简化，因为符合常人思维。如果不是这种特殊的计数模式就不能用十进制来简化了，或者说不能用十进制来理解了。例如，十六进制是0 ~ 9 ~ A ~ F，为什么不是0 ~ 15呢？因为在生活中没有用到，或者很少用到0 - 15 - 0的计数模式，所以将十六进制十进制化是没什么意义的。如果你用十进制来理解十六进制就很奇怪，十进制里可没有A ~ F。

那么进制的计数的规则是什么呢？十进制为什么又会那么特殊？

三、进制的计数规则

进制的计数规则以“1”和“0”为标准，这里的“1”和“0”代表有和无。

例如5个苹果，就是{ “1”，“1”，“1”，“1”，“1” }，用5个单位来记录苹果的数量。不管你是什么进制，这个都是不变的。苹果的数量客观存在，只是表示这些数量的方法和形式可以不同。

二进制表示：101

三进制表示：12

四进制表示：11

分别用二、三、四进制表示5个苹果，尽管表示的形式不同，但是5个苹果就是5个苹果。

为什么十进制如此特殊？

数字最多只有{ 0，1，2，3，4，5，6，7，8，9 }十个，用这些数字表示的进制即为十进制。单个的数字，相信都能理解其含义。

0 { “0” }

1 { “1” }

2 { “1”，“1” }

... ...

9 { “1”，“1”，“1”，“1”，“1”，“1”，“1”，“1”，“1” }

每个数字即表示对应的单位“1”的数量， 数字之间又能排列组合表示更大的数量。

十进制是用纯数字计数的最高进制，换句话说十进制是用纯数字计数最连贯的进制。连贯的含义就是一个接着一个，不会出现跳跃的现象。例如，十进制的12个苹果，就是12个苹果；八进制的12个苹果，则是10个苹果。原因就在于八进制表示的12里面没有8和9两个数字，数字不连贯，导致表示的数量与实际的数量不相等。

所以可以得出十进制是用纯数字表示数量最准确的，没有之一。由于能做到数字的连贯，十进制在生活中很常用，毕竟是符合常人思维。12个苹果就是12个苹果，或者说是12个单位“1”，每个单位“1”都有对应的数字表示。

四、进制相互转换

理解了进制的计数规则，进制之间的相互转换也没什么问题。例如，5用二进制表示为101。

首先要记住一个分组的规则，用n进制表示x，含义为n个“1”为一组，x有几组。很显然就是

x / n = y ···?m

其中y可以叫整组，m可以叫余组。结果为整组 + 余组，整组又可以继续拆成整组 + 余组。

5 / 2 = 2 ··· 1，即为21，而2又可以继续拆分为2 / 2 = 1 ··· 0，得到10。最后用10替换21中的2，得到101。

整组：{ {?“1”，“1”?}，{?“1”，“1”?} }

余组：{?“1”?}

相反，二进制的101是多少，将过程倒过来就行。

首先101中的10是整组 + 余组，即1 * 2 + 0 = 2，用2替换101中的10得到21。21又是整组 + 余组，2 * 2 + 1 = 5，5就是最后的结果。

再举一个八进制的例子，用八进制表示10。

10 / 8 = 1 ··· 2，即为12，12就是最终结果。注意这里不是读作十二，而是读作一二。

反过来，八进制的12是多少。

12即为1 * 8 + 2 = 10，结果是10。

其实不管是多少进制转换成多少进制，首先必须要先转换成十进制，因为我们对十进制很熟悉，更好理解。

五、用计算器计算进制

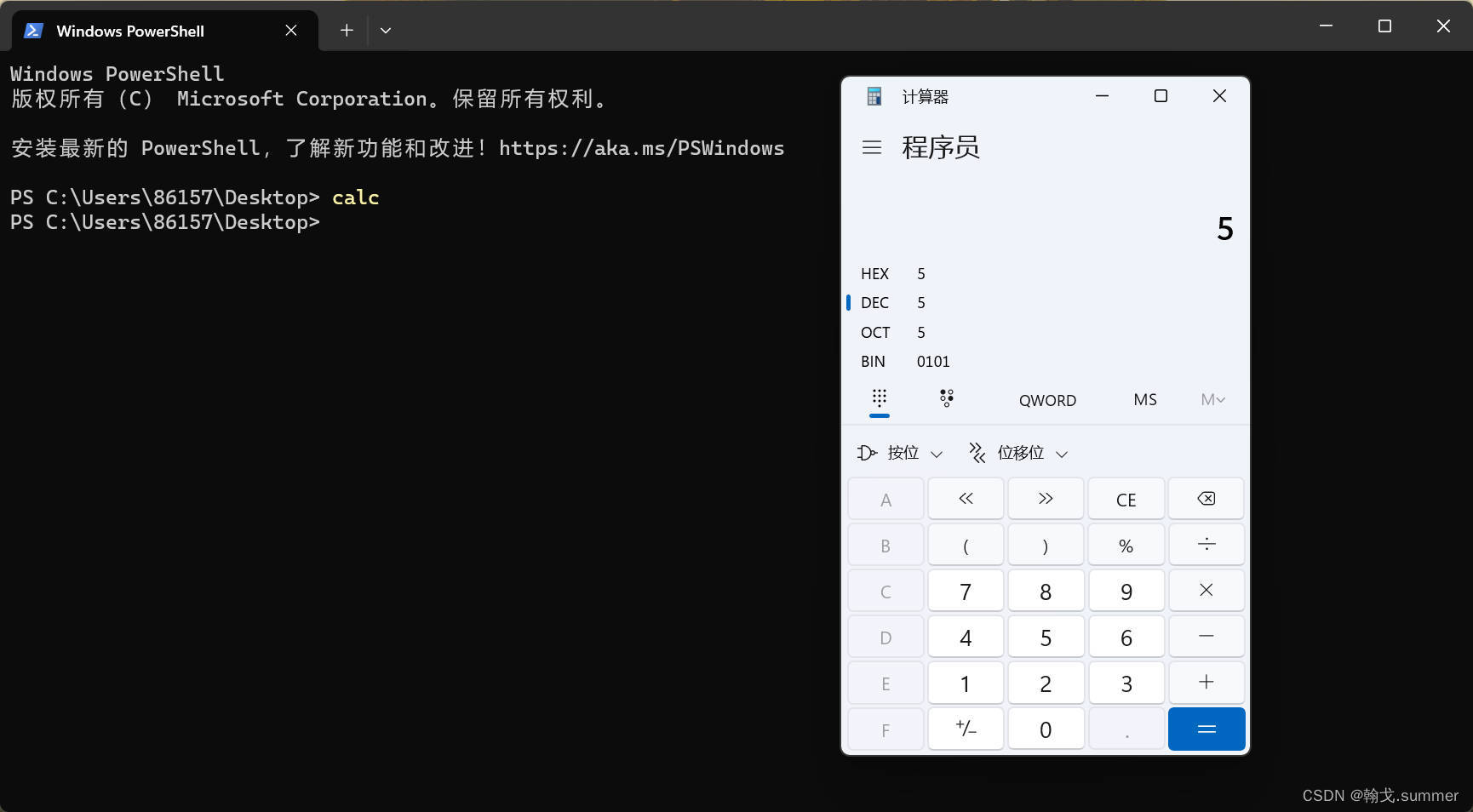
打开电脑上的计算器，如果你不知道你电脑上的计算器在哪，先在桌面右键打开终端，输入calc然后回车。

calc

选择程序员模式

HEX? 十六进制

DEC? 十进制

OCT? 八进制

BIN? ?二进制

六、进制前缀

为了区分进制，会在进制数前面加上前缀以区分。

二进制（BIN）：0b或者0B，例如0b101。

八进制（OCT）：0o或者0O，例如0o12。

十进制（DEC）：没有前缀，例如10。

十六进制（HEX）：0x或者0X，例如0x1A2B。