数据结构和算法-散列查找（哈希查找 哈希函数 处理冲突的方法）

发布时间：2024年01月03日

文章目录

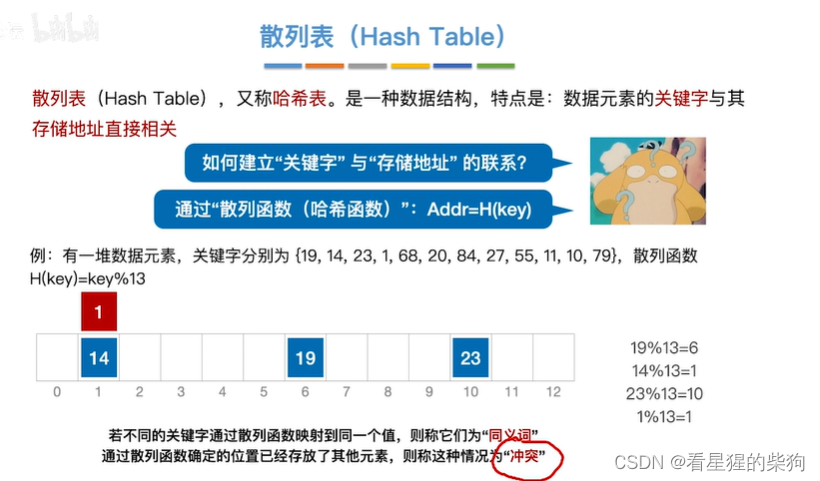
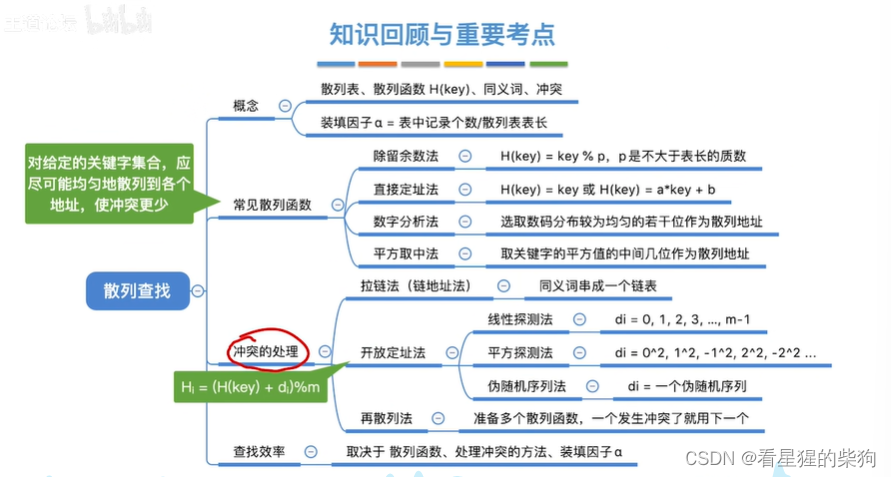
散列表（哈希表）

在这里插入图片描述

处理冲突的方法-拉链法

当出现关键字通过散列函数后对应一个位置时，该位置可存储一个链表，通过链表链接所有同义词，即出现同义词时，链接到链尾或链头
在这里插入图片描述

散列查找

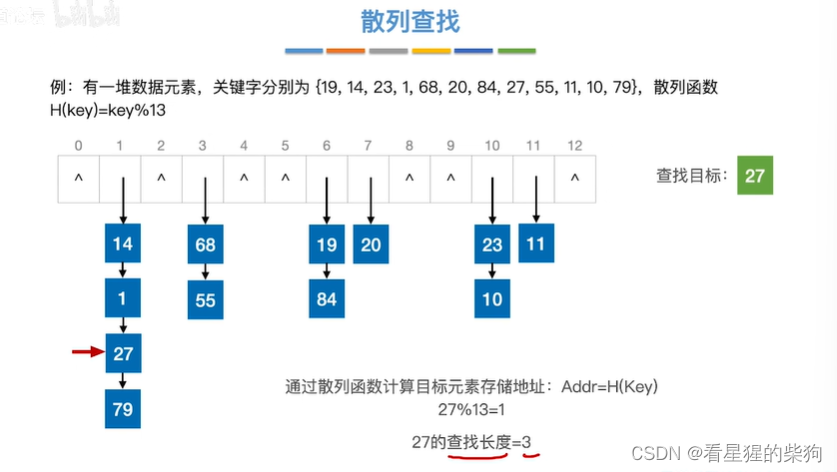
通过散列韩素华计算查找目标在散列表中的位置
当查找27时，通过哈希函数计算其位置为1，到1所对应的链表从头开始寻找
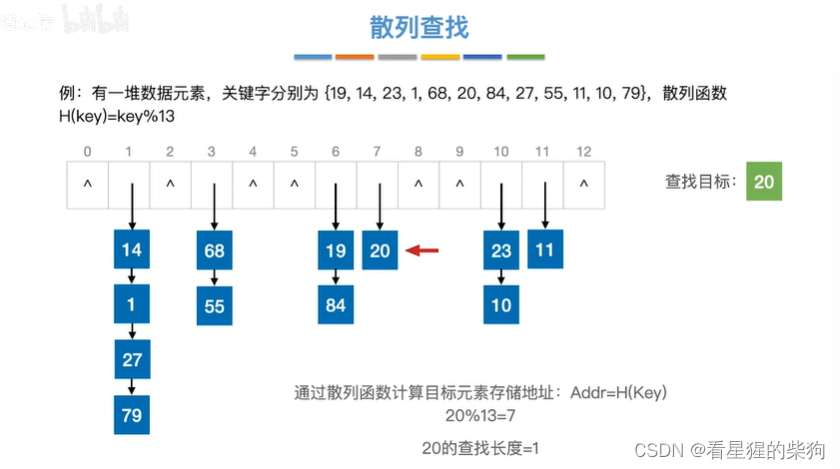
在这里插入图片描述
查找20
在这里插入图片描述
查找21，通过哈希函数找到对应的位置，发现链表为空，所以没有
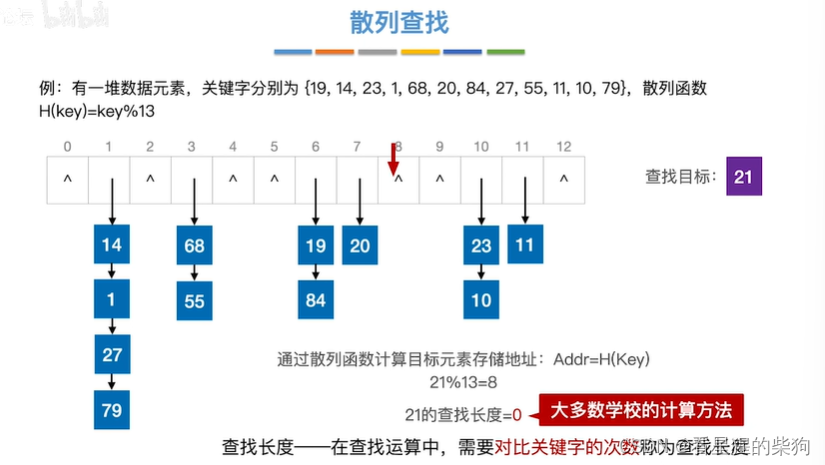
在这里插入图片描述
查找长度参考学校题目
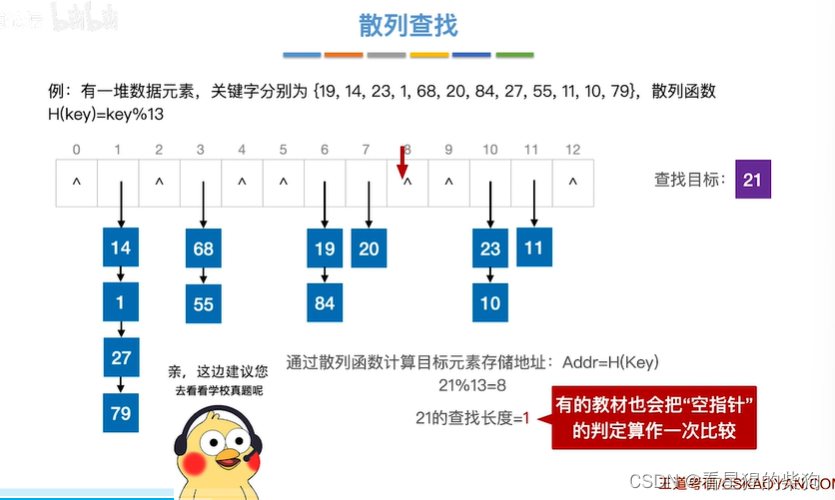
在这里插入图片描述
查找66
在这里插入图片描述

平均查找成功长度

通过一层一层来计算
或者一类一类同义词来计算
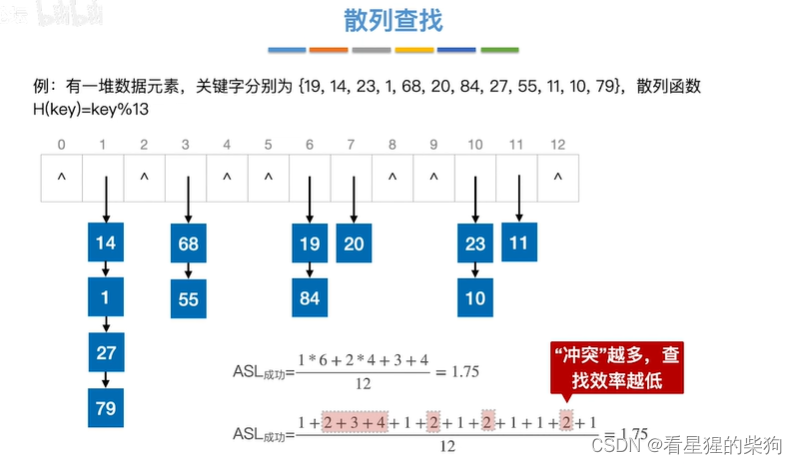
在这里插入图片描述
冲突是指的同义词很多，都占一个位置了所以说冲突
此时如果同义词没有，那么查找长度会低很多
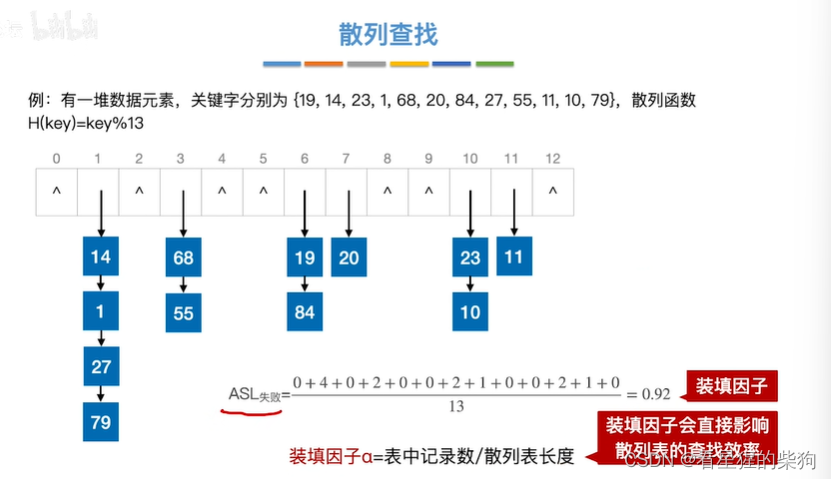
在这里插入图片描述

平均查找失败长度

此时映射到每个位置的概率相等
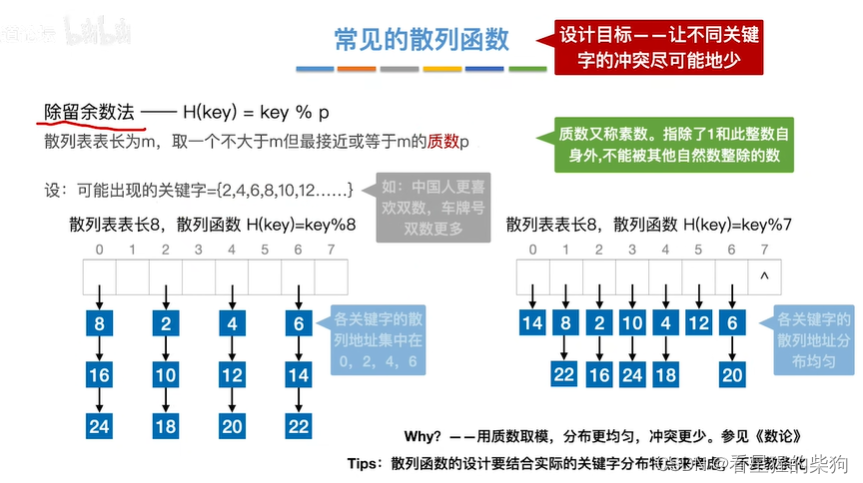
在这里插入图片描述

常见的散列函数

除留取余法

此时发现取质数发现同义词更多了，原因是关键字是连续的
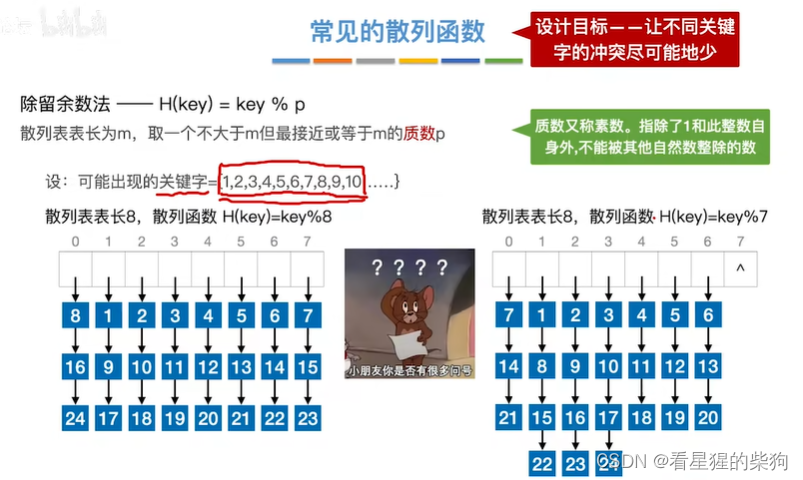
在这里插入图片描述
如果是关键字是偶数较多
在这里插入图片描述

直接定址法

此时直接定址法，如果由于关键字对应的位置也是连续的，所以如果关键字缺少，那么对应的位置的内容也会缺少。此时会造成空位，那么存储空间会浪费

在这里插入图片描述

数组分析法

分布比较均匀，即每个关键字对应的位置可能都不同
在这里插入图片描述

平方取中法

适用于每位取值都不均匀或小于散列地址所需的位数
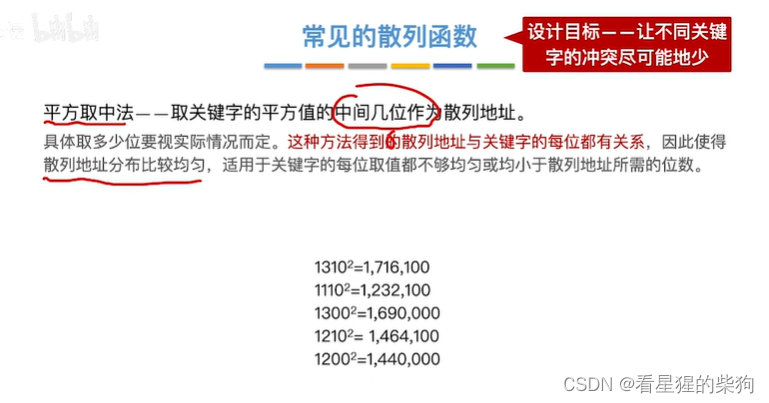
在这里插入图片描述
使得散列地址和关键字每一位都相关

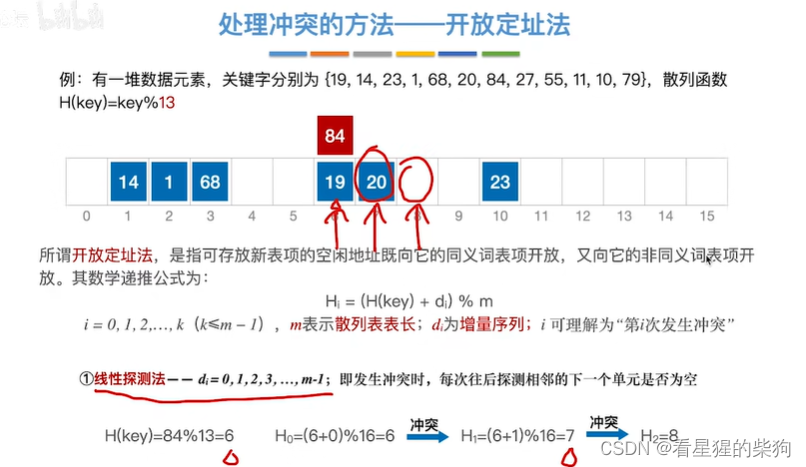
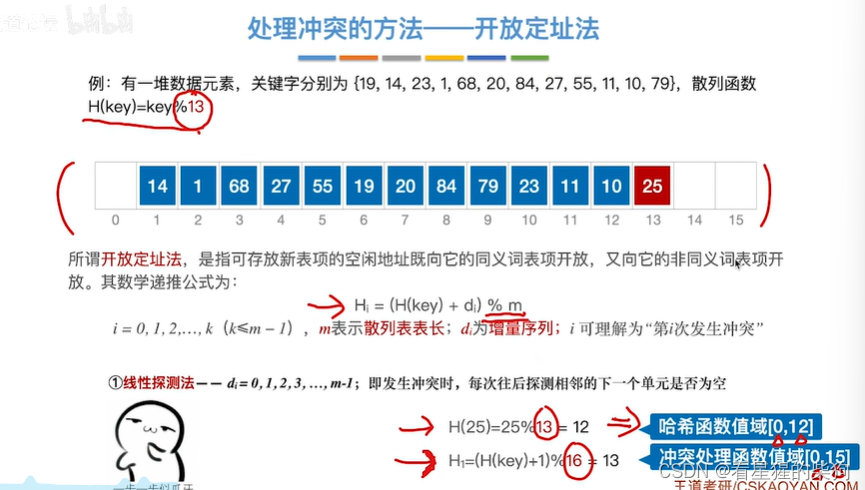
在这里插入图片描述
在这里插入图片描述

处理冲突的方法-开放地址法

此时空闲表的地方既可以存关键字经过哈希函数映射到此的关键字，也可以存不被映射到此的关键字
在这里插入图片描述

线性地址法

此时存1时，出现0次冲突，然后再次计算其对应的哈希表位置，出现1次冲突，再次计算，此时不冲突
在这里插入图片描述
此时存84时，出现0次冲突，然后再次计算其对应的哈希表位置，出现1次冲突，再次计算，此时冲突，再次计算，此时不冲突，注意di都是从0开始的
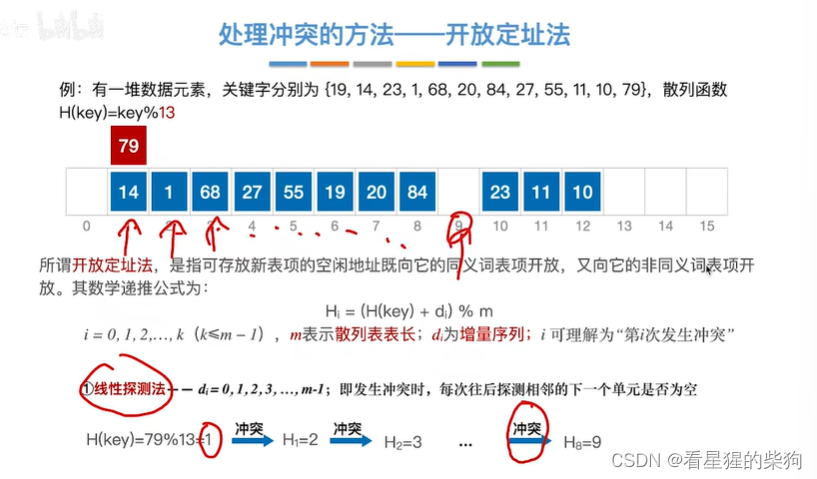
在这里插入图片描述
27同理
在这里插入图片描述
55同理
在这里插入图片描述
10同理
在这里插入图片描述
79同理
在这里插入图片描述
假如此时还存25
此时注意取模的长度不同
在这里插入图片描述

查找操作

查找27
依然需要调用H公式去寻找比对
在这里插入图片描述
查找11在这里插入图片描述
查找21
当比对的空的哈希表位置时，认为查找失败
注意此时需要比较空位置
由于拉链法其实每个哈希表位置存放的是指针，所以不算作对比关键字的次数。而开发地址法存的是和关键字同类型的，所以看作比对关键字
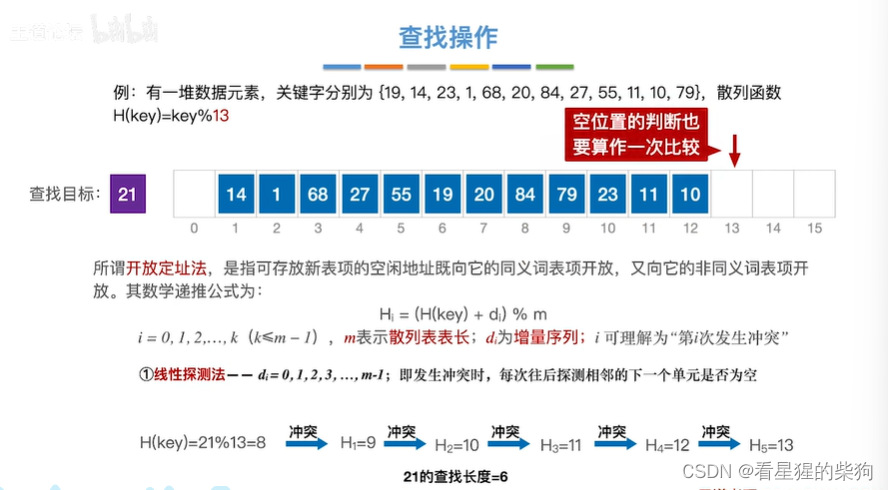
在这里插入图片描述
空位置越早遇到，越早可确定查找失败，同样查找21，下面这种情况只需要比对3次
在这里插入图片描述

删除操作

删除1，如果直接置为空
在这里插入图片描述
此时查找27遇到空，将认为是没有找到，而此时27确是存在的
在这里插入图片描述
所以删除应该做一个删除标记
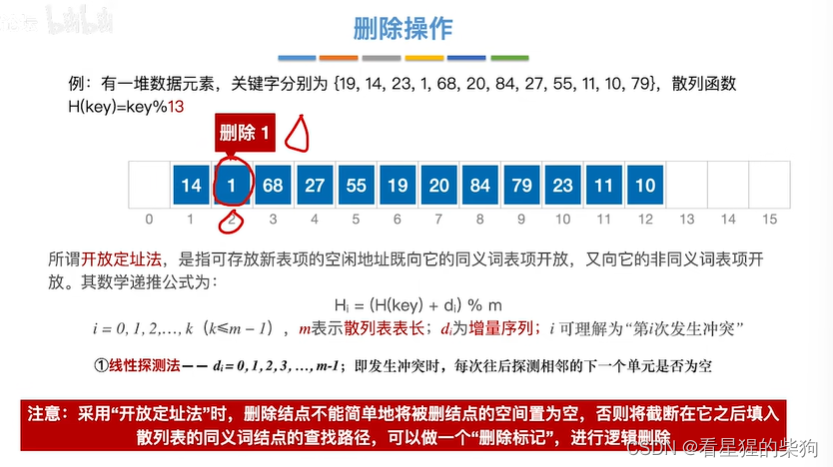
在这里插入图片描述
此时依然可以找到27
在这里插入图片描述
查找79此时由于大量被删除，做了删除标记，但由于仍然需要从0次冲突开始计算，导致浪费时间
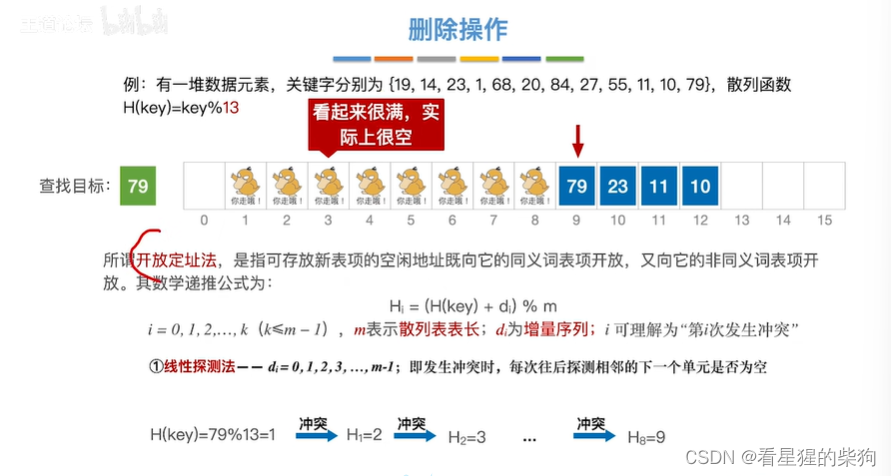
在这里插入图片描述

查找效率分析

平均查找成功长度

在这里插入图片描述

平均查找失败长度

由于对应哈希表位置关键字不对时，需要通过冲突函数向后查找比对
在这里插入图片描述
由于对应关键字冲突是放后面，是连续的，所以容易扎堆聚集
在这里插入图片描述

平方探测法

注意负数的取模操作，余数为正数
此时因为增量序列不是连续的，所以在哈希表中的位置不容易堆积
在这里插入图片描述

查找操作

查找71，由增量序列来查找
在这里插入图片描述

散列表长度要求

表长为偶数发现根据增量序列有重复的散列表位置，并且不能探测到所有位置

在这里插入图片描述

伪随机序列法

伪随机序列是自己定义的增量序列，探测根据伪随机序列探测
在这里插入图片描述
在这里插入图片描述

开放定址法-小结

注意三种增量序列对应的删除都需要做删除标记
在这里插入图片描述

处理冲突的方法-再散列法

就是计算的一个关键字对应的哈希表位置发生冲突就使用下一个哈希函数计算关键字在哈希表中的位置
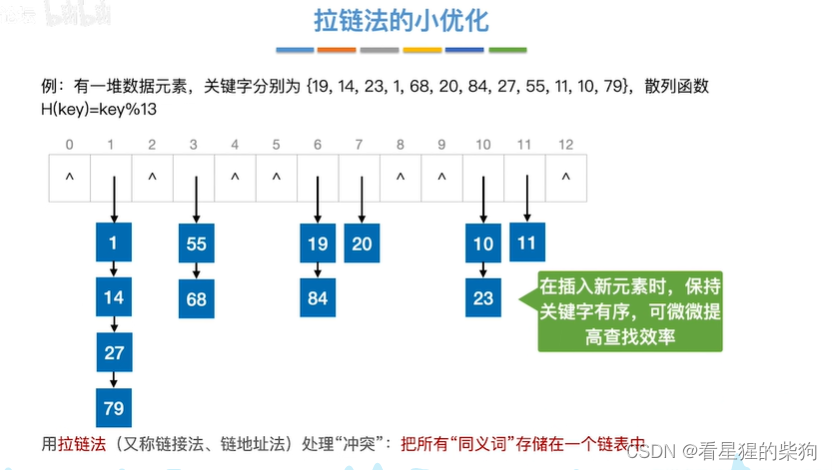
在这里插入图片描述

小结

在这里插入图片描述

拉链法的小优化

提高查找效率，当查找失败时不必每个关键字都比对
在这里插入图片描述

文章来源:https://blog.csdn.net/llovewuzhengzi/article/details/135358027
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章