计算机图形学作业：Weiler-Atherton 裁剪多边形

题目要求：

编写程序，采用 Weiler-Atherton 算法实现多边形对多边形的裁剪，并返回裁剪结果。

?解答：

//每次裁剪结果保存在数组now中并绘制
struct Point2d {
	double x, y;
};
struct Line {
	Point2d start;
	Point2d end;
};

void display(CDC* pDC)//显示裁剪结果
{
	Winit();//初始化裁剪多边形poly2和被裁多边形poly1

	int len1 = poly1.size();//绘制被裁减多边形
	for (int i = 0; i < len1; i++) {
	pDC->MoveTo(poly1[i].x, poly1[i].y);
	pDC->LineTo(poly1[(i + 1) % len1].x, poly1[(i + 1) % len1].y);
	p1.push_back({ {poly1[i].x, poly1[i].y}, {poly1[(i + 1) % len1].x, poly1[(i + 1) % len1].y} });
	}
int len2 = poly2.size();
	for (int i = 0; i < len2; i++) {
	pDC->MoveTo(poly2[i].x, poly2[i].y);
	pDC->LineTo(poly2[(i + 1) % len2].x, poly2[(i + 1) % len2].y);		p2.push_back({ {poly2[i].x, poly2[i].y}, {poly2[(i + 1) % len2].x, poly2[(i + 1) % len2].y} });
	}
	getIntersections(pDC);
}

void getIntersections(CDC* pDC) //求出所有交点，按照顺序存放在新数组中
{
	int len1 = poly1.size();//求出new1
	for (int i = 0; i < len1; i++) {
		new1.push_back(poly1[i]);
		std::vector<Point2d> tmp;
		for (auto it2 : p2) {
			Point2d p = intersection({ {poly1[i].x, poly1[i].y},{poly1[(i + 1) % len1].x, poly1[(i + 1) % len1].y} }, it2);
			if (p.x != -1 && p.y != -1) tmp.push_back({ p.x, p.y });
		}
		sort(tmp.begin(), tmp.end(), [&](Point2d p1, Point2d p2) {
			return dis(p1, poly1[i]) < dis(p2, poly1[i]);
			});
		for (auto it : tmp) new1.push_back(it);
	}

	int len2 = poly2.size();//求出new2
	for (int i = 0; i < len2; i++) {
		new2.push_back(poly2[i]);
		std::vector<Point2d> tmp;
		for (auto it2 : p1) {
		Point2d p = intersection({ {poly2[i].x, poly2[i].y},{poly2[(i + 1) % len2].x, poly2[(i + 1) % len2].y} }, it2);
		if (p.x != -1 && p.y != -1) tmp.push_back({ p.x, p.y });
		}
		sort(tmp.begin(), tmp.end(), [&](Point2d p1, Point2d p2) {
			return dis(p1, poly2[i]) < dis(p2, poly2[i]);
			});
		for (auto it : tmp) new2.push_back(it);
	}
       //不是交点的点对应值为-1
	pos1.resize(new1.size(),-1), pos2.resize(new2.size(),-1);	

for (int i = 0; i < new1.size(); i++) { 
		for (int j = 0; j < new2.size(); j++) {
			if (fabs(new1[i].x - new2[j].x) < 0.1 && fabs(new1[i].y - new2[j].y) < 0.1) {
				pos1[i] = j;
				pos2[j] = i;
			}
		}
	}
	Weilerwork(pDC);
}


void Weilerwork(CDC* pDC)// Weiler-Atherton算法对多边形进行裁剪
{
	CPen NewPen, * pOldpen;
	NewPen.CreatePen(PS_SOLID, 1, RGB(220,20,60));  
	pOldpen = pDC->SelectObject(&NewPen); 

	std::vector<Point2d> now;//当前选择到的点
	int len1 = new1.size();
	int len2 = new2.size();
	Point2d sp;//保存每轮循环开始的进点
	vis1.resize(new1.size(), false), vis2.resize(new2.size(), false);
	for (int i = 0; i < new1.size(); i++) {//new1 新多边形1 new2新多边形2
		if (vis1[i]) continue;
		int ch = 1, nowpos = i;

		if (!isPointInsidePoly(new1[nowpos], poly2) && isPointInsidePoly(new1[(nowpos + 1) % len1], poly2)&&!vis1[nowpos])//进点
		{
			nowpos = (nowpos + 1) % len1;
			now.push_back(new1[nowpos]);
			sp = new1[nowpos];//保存每轮开始的进点
			vis1[nowpos] = true;//去掉进点标志
			nowpos= (nowpos + 1) % len1;
		}
		else continue;
	
while (1) {
//遍历第一个多边形
			if (ch == 1) { 
				now.push_back(new1[nowpos]);
				vis1[nowpos] = true;//访问过，打上标记
				if (pos1[nowpos] == -1)// 不是交点，保存
				{
					nowpos = (nowpos + 1) % len1;
					continue;
				}
	//出点，改沿着裁剪多边形			if (!isPointInsidePoly(new1[(nowpos + 1) % len1], poly2)) 
				{
                                                 ch = 2;
					nowpos = pos1[nowpos];
					nowpos = (nowpos + 1) % len2;
				}
			}
			else {//遍历第二个多边形
				now.push_back(new2[nowpos]);
				if (pos2[nowpos] == -1)//不是交点，保存
				{
					nowpos = (nowpos + 1) % len2;
					continue;
				}

//回到起始的进点，输出已经得到的顶点		if (sp.x - new1[pos2[nowpos]].x < 0.01 && sp.y-new1[pos2[nowpos]].y < 0.01) {
	//绘制交多边形				
	for (int j = 0; j < now.size(); j++) 
{		
pDC->MoveTo(now[j].x, now[j].y);				pDC->LineTo(now[(j + 1) % now.size()].x, now[(j + 1) % now.size()].y);
	}
	now.clear();
	break;
	}
	
if (pos2[nowpos] !=-1&&isPointInsidePoly(new1[(pos2[nowpos]) % len1], poly2))//遇到进点，改沿着被裁减多边形
				{
					ch = 1;
					vis1[pos2[nowpos]] = true;
					nowpos = pos2[nowpos];
					nowpos = (nowpos + 1) % len1;
				}
				else
				{
					nowpos = (nowpos + 1) % len2;
				}
			}
		}
	}
	pDC->SelectObject(pOldpen);
	NewPen.DeleteObject();
}

void Winit()//初始化裁剪多边形poly2和被裁多边形poly1
{

		poly1.clear();
		poly2.clear();
//测试用例
               poly2.push_back({300, 300});
               poly2.push_back({ 400, 300 });
		poly2.push_back({ 400, 400 });
		poly2.push_back({ 300,  400 });

		poly1.push_back({ 310, 200 });
		poly1.push_back({ 350, 200 });
		poly1.push_back({ 350, 350 });
		poly1.push_back({ 330, 280 });
		poly1.push_back({ 310, 340 });

}	

?测试结果：

?

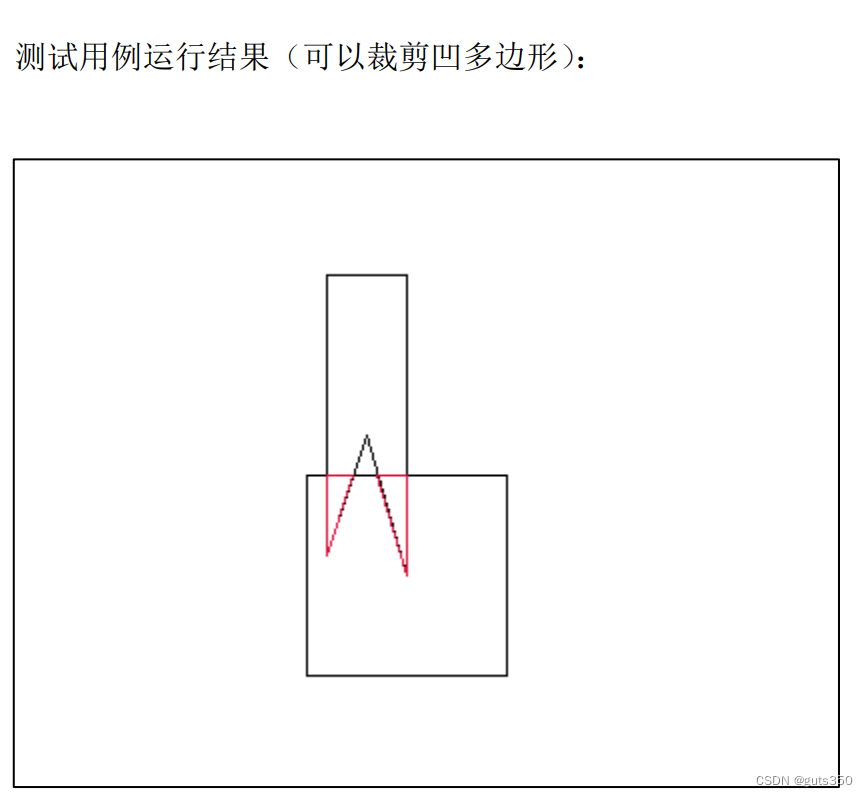
在此文章代码上修改：【Weiler-Atherton算法】 计算机图形学多边形裁剪算法-CSDN博客