非均衡设计评价两个批次的数据一致性
发布时间:2024年01月09日
任务描述
第一批次的药物实验设置了三个剂量(0.2,0.6,1.8)mg/kg,每个剂量水平有十个受试者。
第二批次的药物实验设置了其他三个剂量(1.2,2.4,4.8) mk/kg,每个剂量水平有两个受试者。
问:这两个数据一致性怎么样?
其实我不理解这个一致性如何评价!!!
我理解是不是这两批数据可以用一个方程表示?或者说第二批次数据落在第一批次方程的置信区间内?
数据
getwd()
rm(list=ls())
list.files()
library(tidyverse)
df <- read.table("AUClast1.csv",header = T,sep=",",encoding = "UTF-8")
head(df)

代码
# 重新整理一下数据
dose <- as.numeric(df[,1])
resp <- c(27.33,88.06,351.4,487.5,1046,2520)
df <- as.data.frame(cbind(dose,resp))
df <- df %>% arrange(dose)
head(df)
# dose resp
#1 0.2 27.33
#2 0.6 88.06
#3 1.2 487.50
#4 1.8 351.40
#5 2.4 1046.00
#6 4.8 2520.00
plot(log10(dose),log10(resp))
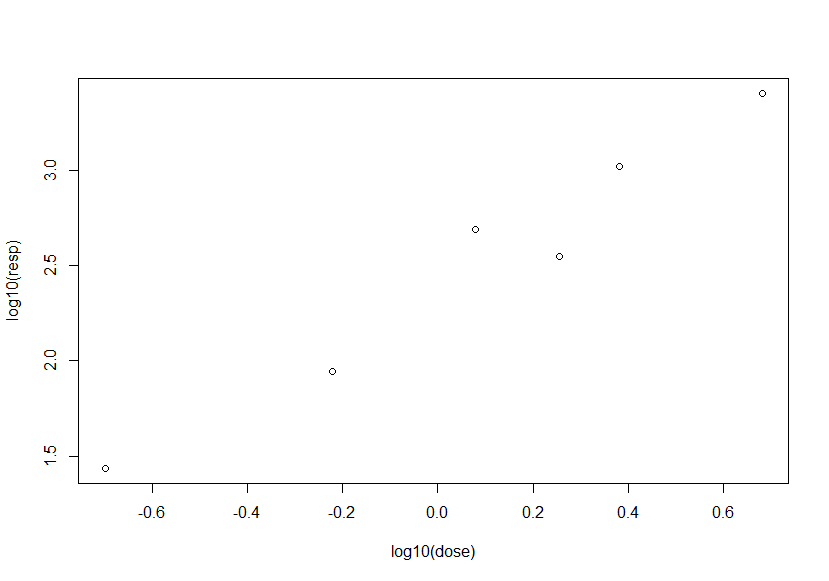
# 散点图可以看到数据取log后基本上是线性相关的,那就做线性拟合好了
# 然后第一批次的数据就三个点,什么正态分布,方差齐性,强影响点,都不考虑了,直接干
# 把第一批的数据拿出来
df1 <- df[c(1,2,4),]
model <- lm(log10(resp)~log10(dose),df1)
summary(model)
# 模型的截距和系数都有意义,继续
Call:
lm(formula = log10(resp) ~ log10(dose), data = df1
Residuals:
1 2 4
0.0155 -0.0310 0.0155
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.2336 0.0252 88.7 0.0072
log10(dose) 1.1623 0.0562 20.7 0.0308
Residual standard error: 0.0379 on 1 degrees of freedom
Multiple R-squared: 0.998, Adjusted R-squared: 0.995
F-statistic: 428 on 1 and 1 DF, p-value: 0.0308
# 用上面的模型预测六个剂量水平的响应值,以及95%的置信区间
p1 <- predict(model,df,interval = "confidence", level = 0.95)
p1
# fit lwr upr
#1 1.421 0.9813 1.861
#2 1.976 1.6976 2.254
#3 2.326 1.9741 2.677
#4 2.530 2.0905 2.970
#5 2.676 2.1635 3.188
#6 3.025 2.3231 3.728
# 把dose,response,fit,lwr,upr构造一个数据框作图
df <- cbind(df,p1)
df %>%
ggplot(aes(x = log10(dose), y = log10(resp))) +
geom_point(colour = "midnightblue", alpha = 0.5,size=1) +
geom_line(aes(y = lwr), lty = 2,color = "blue") +
geom_line(aes(y = upr), lty = 2,color = "green") +
labs(x = "log10(Dose)", y = "log10(Response)", color = NULL) +
theme_test()
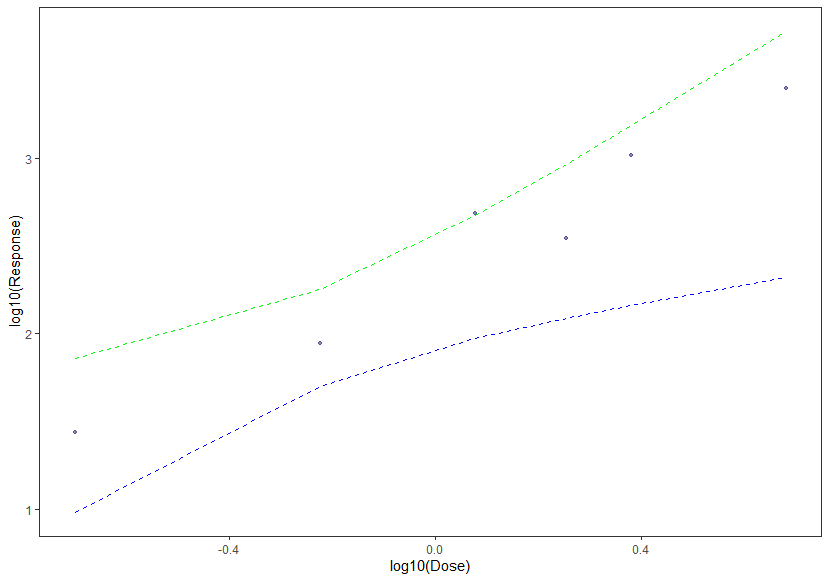
# 置信区间用色带表示
# 坐标轴改一下
# fit值用红线表示
# 真实数据点 用散点表示
dose02 <- as.numeric(df[1,2:11])
dose06 <- as.numeric(df[2,2:11])
dose18 <- as.numeric(df[3,2:11])
dose12 <- as.numeric(df[4,12:13])
dose24 <- as.numeric(df[5,12:13])
dose48 <- as.numeric(df[6,12:13])
df2 <- cbind(rep(0.2,10),dose02)
df2 <- rbind(df2,cbind(rep(0.6,10),dose06))
df2 <- rbind(df2,cbind(rep(1.2,2),dose12))
df2 <- rbind(df2,cbind(rep(1.8,10),dose18))
df2 <- rbind(df2,cbind(rep(2.4,2),dose24))
df2 <- rbind(df2,cbind(rep(4.8,2),dose48))
df2 <- as.data.frame(df2)
colnames(df2) <- c("dose","resp")
df <- merge(df2,df,all.x = T,by = "dose")
xlabs <- unique(df$dose)
ylabs <- unique(df$resp.y)
head(df,10)
# dose resp.x resp.y fit lwr upr
#1 0.2 24.9 27.33 1.421 0.9813 1.861
#2 0.2 19.7 27.33 1.421 0.9813 1.861
#3 0.2 27.3 27.33 1.421 0.9813 1.861
#4 0.2 26.8 27.33 1.421 0.9813 1.861
#5 0.2 30.8 27.33 1.421 0.9813 1.861
#6 0.2 30.2 27.33 1.421 0.9813 1.861
#7 0.2 31.5 27.33 1.421 0.9813 1.861
#8 0.2 22.5 27.33 1.421 0.9813 1.861
#9 0.2 24.6 27.33 1.421 0.9813 1.861
#10 0.2 35.0 27.33 1.421 0.9813 1.861
df %>%
ggplot(aes(x = log10(dose), y = fit)) +
geom_line(colour = "red", alpha = 0.5) +
geom_point(aes( y = log10(resp.x)),color="darkblue")+
geom_ribbon(aes(ymin = lwr, ymax = upr), fill = "blue", alpha = 0.3)+
labs(x = "Dose,mg/kg", y = "AUG_last.(h*ug/mL)", color = NULL) +
scale_x_continuous(breaks = log10(xlabs),labels = xlabs)+
scale_y_continuous(breaks = log10(ylabs),labels = ylabs)+
theme_test()+
labs(title = "AUC-dose relationship")
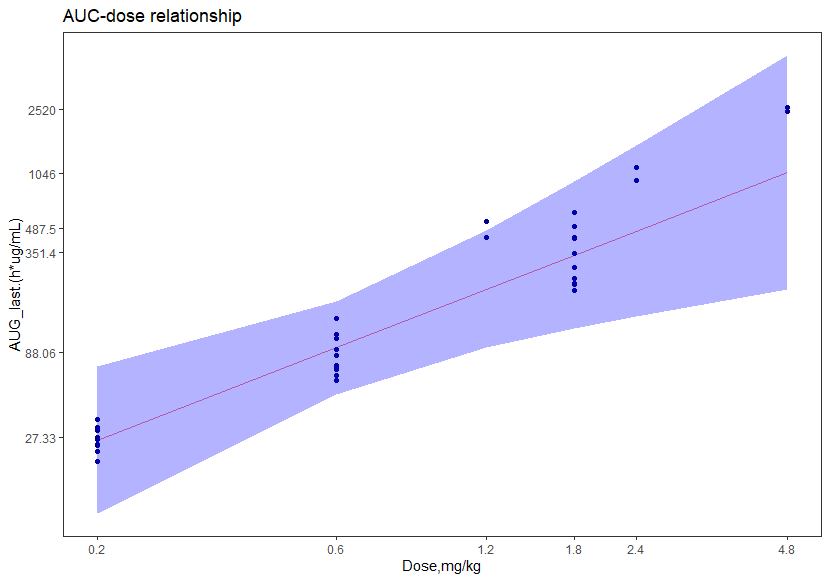
结论
使用第一批数据拟合的方程,用于预测第二批次数据,使用第二批次的剂量作为因变量,在95%的置信区间内,第二批次的response落在了预测区间内。
凑合能说第二个批次的数据 与 第一批数据具有一致性。
文章来源:https://blog.csdn.net/jiangshandaiyou/article/details/135480789
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- AOP(面向切面编程)基于XML方式配置
- 03.分支结构
- springboot的配置文件,以及spring boot自动装配的原理,bean的管理。
- 微信小程序有几个文件
- 微信小程序生成二维码海报并分享
- Delete `?`eslint(prettier/prettier)
- HAL——点灯
- 劲松中西医结合医院主任谭巍谈生殖感染对夫妻的四大影响
- 前端常用数据处理方法-2
- And. And. And. And. And. 会导致 Google Docs 崩溃