扩散模型介绍
介绍
AI 绘画中的扩散模型是近年来在计算机视觉和图像生成领域中获得关注的一种深度学习方法。这种模型特别擅长于生成高质量的图像,包括艺术作品和逼真的照片样式的图像。扩散模型的关键思想是通过一个渐进的、可逆的过程将数据(在这个场景中是图像)从有序状态转换到无序状态,然后再逆转这个过程来生成新的数据。
原理
https://readpaper.com/pdf-annotate/note?pdfId=4557071478495911937¬eId=1833652073759793152
- 前向过程(Forward Process) 在前向过程中,模型逐渐地将图像中的信息“扩散”或“腐蚀”掉,最终转换成噪声。这个过程通常是通过向图像中逐步添加高斯噪声来实现的,直到整个图像完全变成随机噪声。
- 逆向过程(Reverse Process) 逆向过程是前向过程的反向操作。模型尝试从随机噪声中重建原始图像,这通常是通过训练神经网络来实现的。神经网络学习如何逐步从噪声中“去除”噪声,最终恢复出清晰的图像。
加噪过程(前向过程)

在上图中,您可以看到扩散模型中加噪过程的可视化表示。这个序列展示了一个清晰、结构化的图像如何逐渐变得更加嘈杂和失真,直到最终变成完全的噪声。
- 第一幅图显示了一个清晰且可识别的对象或场景。
- 随后的图像展示了不断增加的噪声和失真水平。
- 最后一幅图仅仅是随机噪声。
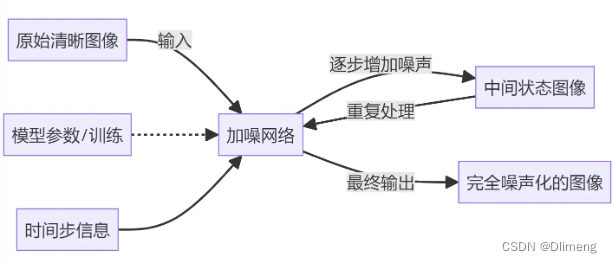
- 原始清晰图像:加噪过程的起点,是初始的清晰图像。
- 加噪网络:通常是一个深度神经网络,负责对清晰图像逐步增加噪声。
- 中间状态图像:每个加噪步骤后的图像状态,逐渐从清晰图像向噪声图像转变。
- 完全噪声化的图像:加噪过程的最终产物,完全由噪声构成。
- 模型参数/训练:表示神经网络的训练过程,这对于学习如何有效地加噪至关重要。
- 时间步信息:在加噪过程中,不同的时间步可能需要不同的处理方式,这通常作为额外信息输入到加噪网络中。
数学公式
1.初始状态:从原始数据 ( x_0 )(例如一张清晰图像)开始。
2.逐步加噪:在每个时间步 ( t ),按照预定义的噪声计划向数据添加噪声,这通常是通过应用高斯噪声来实现的。
x
t
=
α
t
x
t
?
1
+
1
?
α
t
?
x_t = \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \epsilon
xt?=αt??xt?1?+1?αt???
x
t
x_t
xt? 表示第t步加噪后的数据。
α
t
\alpha_t
αt?是时间步 t 处的噪声水平系数,控制噪声的加入量。
x
t
?
1
x_{t-1}
xt?1?是前一步的数据。
?
\epsilon
?是从标准正态分布中采样的随机噪声。
3.最终状态:经过多个时间步后,数据变为纯噪声 x T x_T xT?
关键点
- 扩散模型的核心是学习如何从纯噪声 ( x_T ) 重建原始数据 ( x_0 )。
- 在实际应用中,这通常是通过训练深度神经网络来学习数据的潜在表示并逆转噪声化过程来实现的。
代码实现
## 假设您已有一个图像张量 x_0(比如从图像文件中加载并转换为张量),下面是如何实现加噪过程的示例代码:
import torch
def add_noise(x, t, beta_min, beta_max):
"""
加噪过程
:param x: 原始图像张量
:param t: 当前时间步
:param beta_min: 噪声增加的最小系数
:param beta_max: 噪声增加的最大系数
:return: 加噪后的图像
"""
# 计算噪声比例 alpha
N = 1000 # 假设扩散步骤总数
beta_t = beta_min + (t / N) * (beta_max - beta_min)
alpha_t = 1 - beta_t
# 计算加噪后的图像
noise = torch.randn_like(x)
x_t = torch.sqrt(alpha_t) * x + torch.sqrt(1 - alpha_t) * noise
return x_t
# 示例:假设原始图像 x_0 是一个 PyTorch 张量
x_0 = torch.randn(1, 3, 256, 256) # 一个示例图像张量,大小为 256x256,3通道
# 对图像进行加噪
t = 500 # 当前时间步,比如 500
x_t = add_noise(x_0, t, beta_min=0.1, beta_max=0.2) # 应用加噪函数
去噪过程 (逆向过程)

在这组图像中,您可以看到 AI 图像生成中去噪过程的可视化表示。这个序列展示了一个噪声多、结构不清的图像如何逐渐变得更加清晰和定义,直到最终转变成一个连贯且可识别的场景或对象。
- 第一幅图显示了随机噪声。
- 随后的图像展示了噪声水平的逐渐减少和图像清晰度及结构的增加。
- 最后一幅图清晰且可识别。
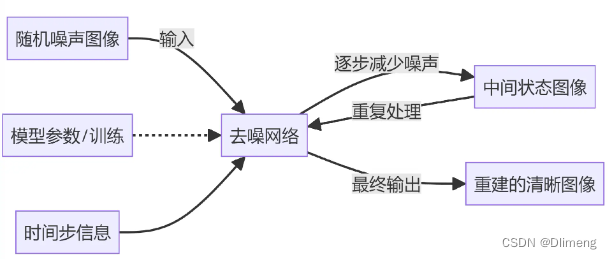
- 随机噪声图像:去噪过程的起点,是加噪过程结束时的状态。
- 去噪网络:通常是一个深度神经网络(如 UNet),负责处理带噪声的图像并逐渐去除噪声。
- 中间状态图像:每个去噪步骤后的图像状态,逐渐从噪声图像向原始图像转变。
- 重建的清晰图像:去噪过程的最终产物,尽可能接近原始图像。
- 模型参数/训练:表示神经网络的训练过程,这对于学习如何有效去噪至关重要。
- 时间步信息:在去噪过程中,不同的时间步可能需要不同的处理方式,这通常作为额外信息输入到去噪网络中。
数学公式
在去噪过程中,一个关键的步骤是根据当前的噪声状态和模型的预测来恢复数据的原始状态。数学上,这可以表示为:
x t ? 1 = 1 α t ( x t ? 1 ? α t 1 ? α ˉ t ? θ ( x t , t ) ) x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta(x_t, t) \right) xt?1?=αt??1?(xt??1?αˉt??1?αt???θ?(xt?,t))
(
x
t
?
1
)
( x_{t-1} )
(xt?1?) 是上一时间步的重建状态。
(
x
t
)
( x_t )
(xt?) 是当前时间步的状态。
(
α
t
)
( \alpha_t )
(αt?) 和
(
α
ˉ
t
)
( \bar{\alpha}_t )
(αˉt?) 是与时间步相关的噪声级别参数。
(
?
θ
(
x
t
,
t
)
)
( \epsilon_\theta(x_t, t) )
(?θ?(xt?,t))是由模型参数为
(
θ
)
( \theta )
(θ)预测的噪声。
关键点
- 逆向过程涉及到一个复杂的深度学习模型,通常是一个条件生成网络,它通过学习在前向过程中应用的噪声模式来实现去噪。
- 模型训练的目标是最小化重建数据和原始数据之间的差异。
- 在扩散模型中,UNet 通常被用作去噪网络,负责从每个时间步的噪声图像中预测原始图像的噪声。它通过逐步减少噪声来逆转前向过程,最终重建出清晰的图像。UNet 的高效特征提取和融合能力是实现这一目标的关键。
去噪过程是一个非常精细和复杂的操作,涉及到大量的迭代和反向传播,以确保重建的数据尽可能接近原始数据。在实际应用中,这需要大量的数据和计算资源。
代码实现
import torch
import torch.nn as nn
class DenoisingModel(nn.Module):
def __init__(self):
super(DenoisingModel, self).__init__()
# 定义 UNet 或其他适合的模型结构
# 例如: self.unet = UNet()
def forward(self, x, t):
# x 是带噪声的图像,t 是时间步信息
# 返回去噪后的图像
# 例如: return self.unet(x, t)
# 示例: 假设 x_T 是最后的噪声状态图像张量
x_T = torch.randn(1, 3, 256, 256) # 一个示例噪声图像张量
# 初始化模型和优化器
model = DenoisingModel()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
# 假设的去噪过程
for t in reversed(range(0, 1000)): # 假设1000个时间步
optimizer.zero_grad()
# 生成模型的输入(需要自己定义如何融合时间步信息)
model_input = torch.cat([x_T, get_timestep_embedding(t)], dim=1)
# 执行去噪
x_pred = model(model_input, t)
# 定义损失函数(需要自己定义适合的损失函数)
loss = compute_loss(x_pred, x_T)
# 反向传播和优化
loss.backward()
optimizer.step()
- DenoisingModel 类:这是去噪模型的定义,通常是一个深度学习模型如 UNet。
- forward 方法:该方法定义了如何使用模型进行去噪。
- x_T:这是加噪过程结束时的噪声图像。
- 时间步信息 t 用于告诉模型当前处理的时间步,这对于模型决定如何去噪很重要。
- 损失函数 compute_loss 和优化器 optimizer 用于训练模型。
扩散模型 和 GAN 区别
| 区别点 | 扩散模型 | GAN |
|---|---|---|
| 工作机制 | 基于逆过程逐步还原真实数据分布 | 包含生成器与判别器的对抗框架 |
| 训练方式 | 最大化似然估计 | 最小化判别器损失,最大化生成器损失 |
| 生成样本质量 | 质量较高,接近真实分布 | 质量参差不齐,易产生模式崩溃 |
| 训练稳定性 | 训练较为稳定 | 训练难度较大,需要精心设计 |
| 优势 | 样本质量好,训练稳定 | 可以学习更复杂分布 |
| 劣势 | 学习能力较弱 | 样本质量不稳定,训练困难 |
图像生成的应用
扩散模型在图像生成方面的应用包括但不限于:
- 艺术创作:生成新的艺术图像,展现独特的风格和创意。
- 数据增强:为机器学习模型训练生成额外的训练数据。
- 风格转换:将一种图像的风格应用到另一种图像上。
- 图像修复和编辑:修复受损的图像或进行创意编辑。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 基于springboot的体育馆使用预约平台的设计与实现
- Redis-redis.conf配置文件中的RDB与AOF持久化方式的详解与区别
- Golang 三数之和+ 四数之和 leetcode15、18 双指针法
- 世微 AP2402 DC-DC降压恒流驱动IC 刹车灯 半亮 高亮瀑闪线路图
- C++重新认知:namesapce
- 快速选择算法
- 如何运用IP定位技术保障网络安全?
- CMMI、SPCA、CSMM,三种认证的差异有哪些?
- flex布局中滚动条展示内容时部分内容无法显示
- LCR 149. 彩灯装饰记录 I