基于优化的规划方法 - 数值优化基础 Frenet和笛卡尔的转换 问题建模 实现基于QP的路径优化算法

发布时间：2023年12月29日

本文讲解基于优化的规划算法，将从以下几个维度讲解：数值优化基础、Frenet与Cartesian的相互转换、问题建模OSQP

1 数值优化基础

1.1 优化的概念

一般优化问题公式：
在这里插入图片描述
f ( x ) f(x) f(x)：目标/成本函数
x x x：决策变量
S S S：可行域 | 约束集
在这里插入图片描述
Example:
A点是最优值
在这里插入图片描述
全局最优和局部最优的概念：
在这里插入图片描述

1.2 无约束优化

在这里插入图片描述

当函数f可微，要成为局部最小值的必要条件是 ▽ f ( x ) = 0 \bigtriangledown f(x)=0 ▽f(x)=0

用梯度方法解决无约束优化问题
（1）梯度下降法
（2）牛顿法
（3）高斯牛顿法
（4）Levenberg-Marquardt 法

通用框架
（1）迭代公式： x ( k + 1 ) = x ( k ) + α ( k ) △ x ( k ) x^{(k+1)}=x^{(k)}+\alpha^{(k)}\bigtriangleup x^{(k)} x(k+1)=x(k)+α(k)△x(k)，采取一步后， f ( x ( k + 1 ) ) < f ( x ( k ) ) f(x^{(k+1)})<f(x^{(k)}) f(x(k+1))<f(x(k))

△ x \bigtriangleup x △x：下降方向
α \alpha α：步长

（2）重复迭代步骤，直到满足停止标准
在这里插入图片描述
步长通过线性搜索来决定
在这里插入图片描述
非精确线性搜索方法：回溯法
在这里插入图片描述

1.2.1用梯度方法解决无约束优化问题 - 梯度下降法：一阶方法，只用到一阶信息

在这里插入图片描述
（1）梯度下降法依赖于成本函数的值再负梯度方向上下降最快。（对于可微成本函数）
（2）使用迭代框架，从起点 x 0 x_0 x0?开始，每个步骤都朝着负梯度的方向前进
在这里插入图片描述

1.2.2用梯度方法解决无约束优化问题 - 牛顿法：二阶方法，用到二阶信息

在这里插入图片描述
通过不断二次函数逼近原函数去找到局部最优
在这里插入图片描述
与梯度下降不一样的地方就是上图的第五行
用牛顿法要求函数二阶可导

1.2.3 用梯度方法解决无约束优化问题 - 高斯 - 牛顿法

高斯-牛顿法是一种优化算法，用于最小化成本函数，该函数写成平方和（最小二乘）
在这里插入图片描述
（1）考虑向量值函数的最小化
在这里插入图片描述
（2）对 F F F做一阶泰勒展开
在这里插入图片描述
（3）解决以下的问题得到 δ \delta δ
在这里插入图片描述
（4）Gauss-Newton 搜索方向 δ = ? ( J T J ) ? 1 J T F \delta =-(J^TJ)^{-1}J^TF δ=?(JTJ)?1JTF
在这里插入图片描述

1.2.4 用梯度方法解决无约束优化问题 - L-M法

（1）对于高斯-牛顿法，可能会发生 J T J J^TJ JTJ是奇异矩阵或者是近似程度不高的病态条件。此时下降方向的稳定性较差，导致算法发散
（2）LM法在梯度下降和高斯牛顿法之间通过参数 λ \lambda λ的影响进行调整
在这里插入图片描述
在这里插入图片描述

1.3 二次规划QP
凸函数和凸集

#pic_center

凸优化问题：

在这里插入图片描述
f 0 , f 1 , . . . , f m f_0,f_1,...,f_m f0?,f1?,...,fm?都是凸函数

（1）可行域是凸的
（2）局部最优解就是全局最优解
（3）理论上和实践上，相对好解决

在这里插入图片描述
凸优化问题的层次结构：

LP：线性规划
QP：二次规划
SOCP：二阶锥规划
SDP：半正定规划
CP：锥规划

QP

在这里插入图片描述
P：半正定矩阵
二次规划的所有约束都是线性的
在这里插入图片描述
图中 P P P就是一个可行集，就是 G x ≤ h Gx≤h Gx≤h

QP求解器

OSQP
在这里插入图片描述
在这里插入图片描述
就是把 P , q , A , l , u P,q,A,l,u P,q,A,l,u矩阵全部定义好，调用求解器

1.4 非线性规划 NLP

在这里插入图片描述
目标函数和约束都是非凸的
求解NLP的方法：
（1）序列二次规划 SQP：把复杂问题拆分成一个一个小的QP问题，依次求解每个QP问题，通过外层迭代找到复杂问题的最优解
（2）内点法 IPM：先找到可行集的内点，从这个点开始迭代，迭代过程中不断去搜索可行域达到最终满足约束的最优解

非线性优化求解器 Ipopt

Ipopt（内点优化器）：用于大规模非线性优化的开源软件包。可用于解决如下形式的一般非线性规划问题
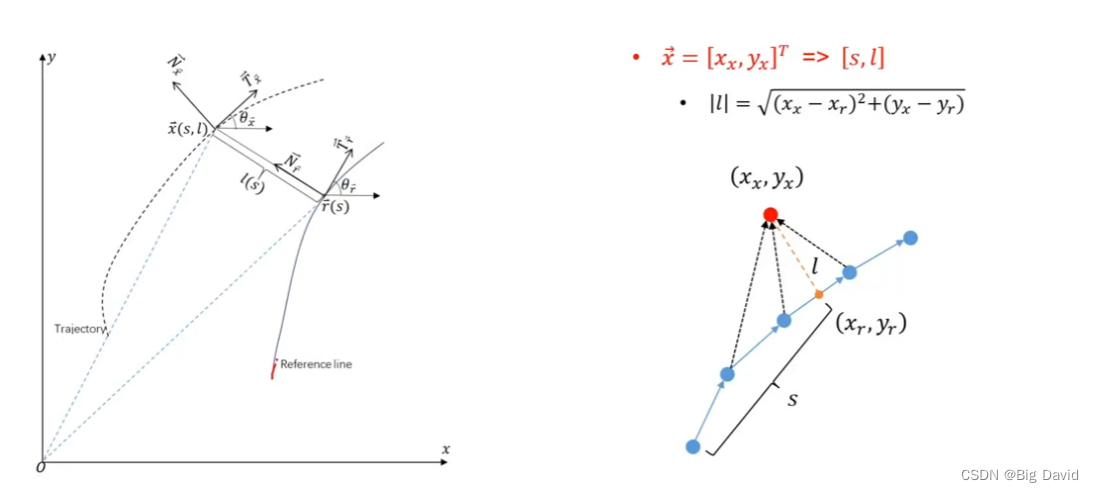
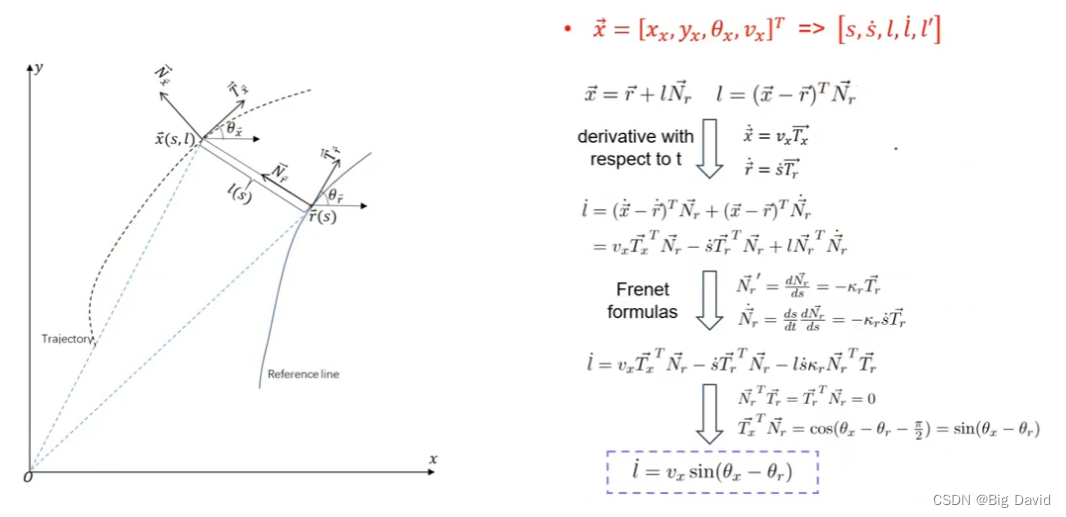
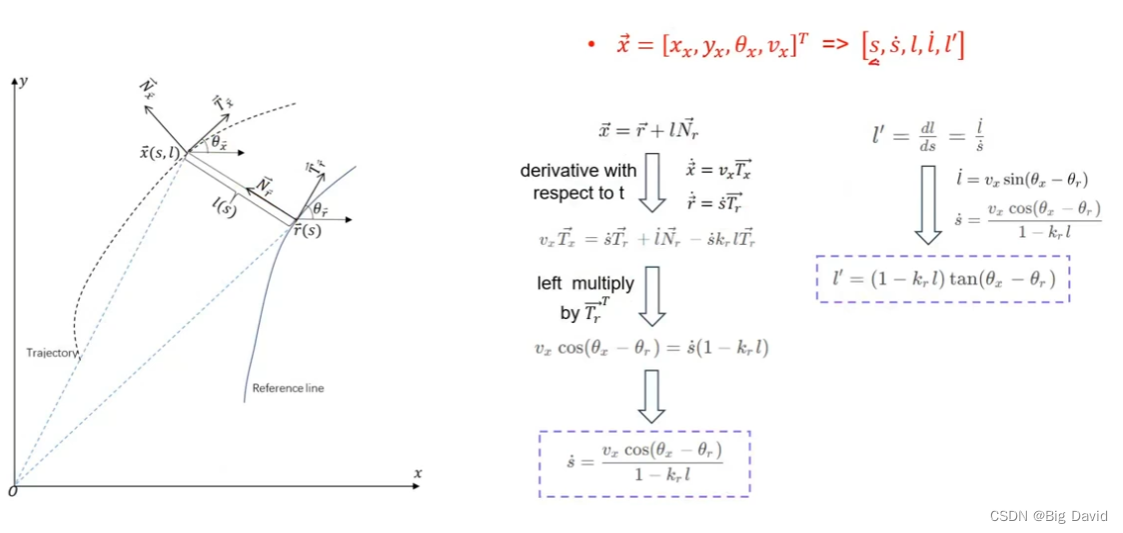
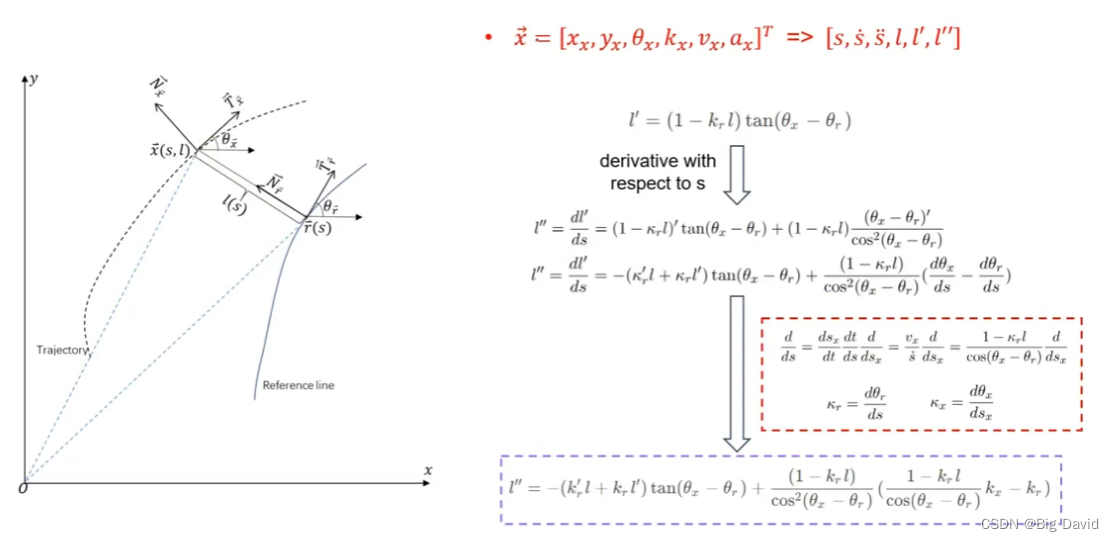
在这里插入图片描述

2 Frenet与Cartesian的相互转换

路径优化在Frenet坐标系下
在这里插入图片描述

状态转换（Frenet | Cartesian）

在这里插入图片描述
在这里插入图片描述
Frenet坐标系
在这里插入图片描述
找投影点 ( x r , y r ) (x_r,y_r) (xr?,yr?)
利用点乘法
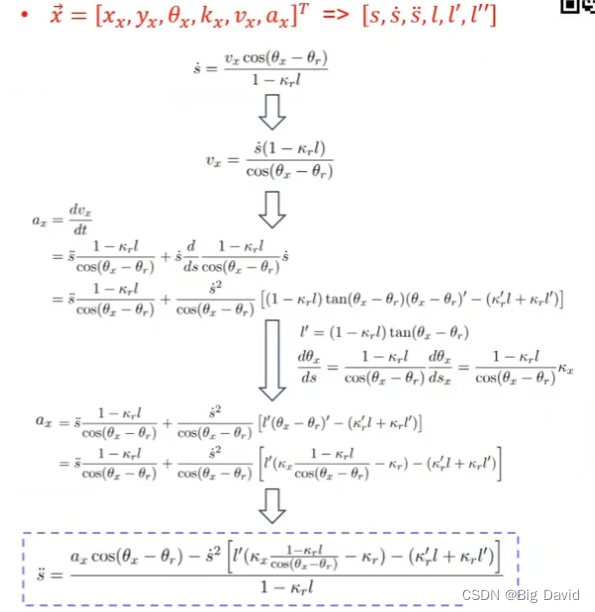
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
总结：

在这里插入图片描述

https://github.com/ApolloAuto/apollo/blob/master/modules/common/math/cartesian_frenet_conversion.cc

在这里插入图片描述

3 问题建模

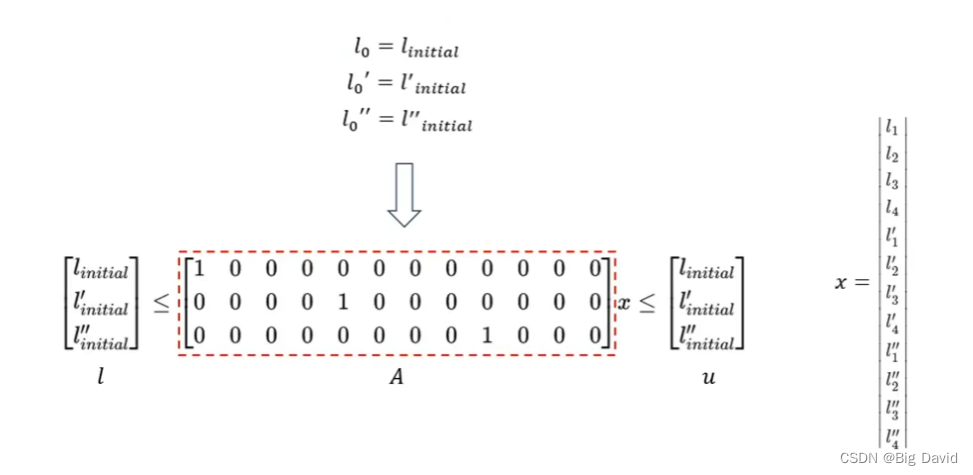
（1）定义优化变量
在这里插入图片描述
根据空间参数离散化路径函数 l ( s ) l(s) l(s)到某个分辨率 Δ s \Delta s Δs，并用这些离散点控制路径的形状
在这里插入图片描述
使用恒定的三阶导数连接连续的离散点
在这里插入图片描述
（2）最优性建模
在这里插入图片描述
1 无碰撞：与环境中的障碍物不相撞
2 最小横向偏差：在不影响安全性的情况下尽可能靠近车道中心线
3 最小的横向运动：横向运动尽可能平缓
4 最大障碍物距离：保持对环境中障碍物的距离

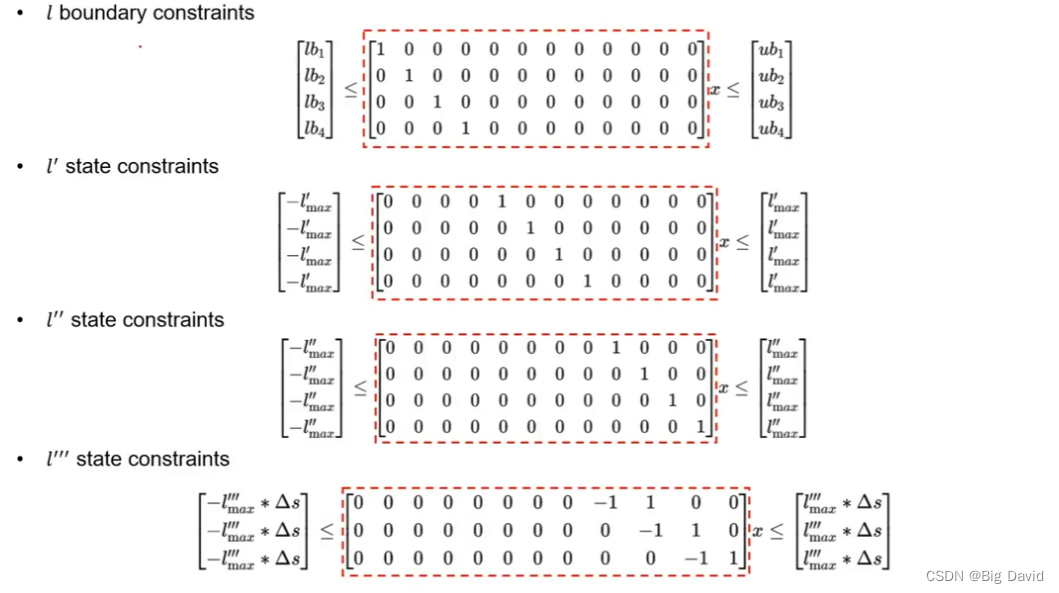
在这里插入图片描述
（3）约束的设计
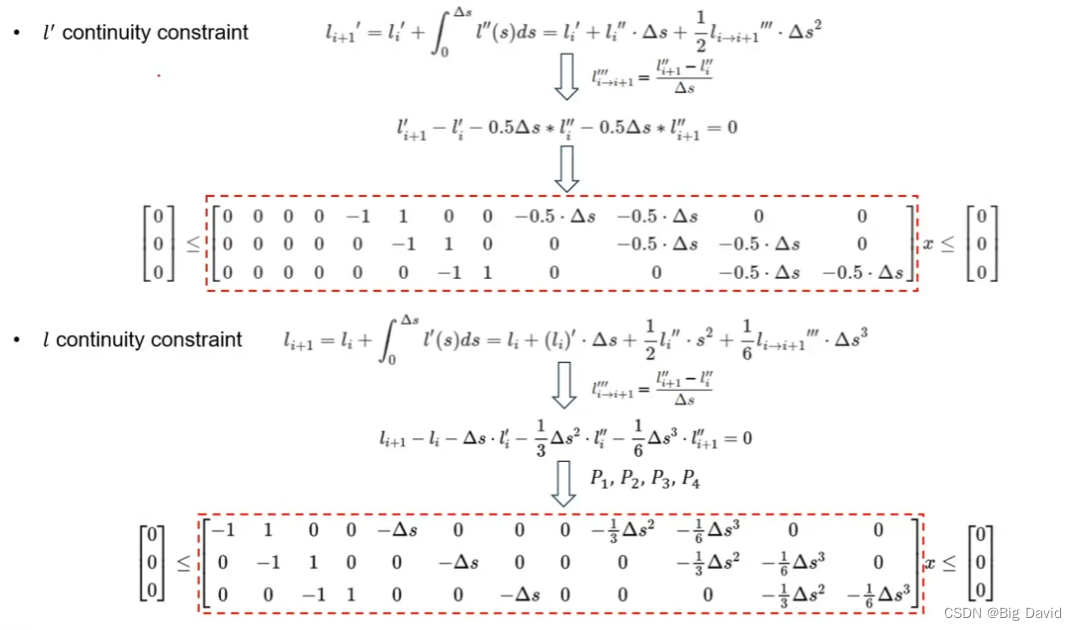
1、连续性约束
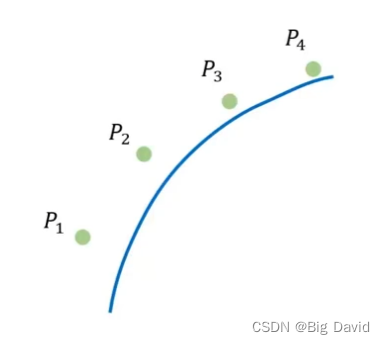
在这里插入图片描述
2、初始状态约束
在这里插入图片描述
3、状态约束
在这里插入图片描述
4、最大曲率约束
在这里插入图片描述
问题建模
在这里插入图片描述
Use OSQP
在这里插入图片描述
给定四个点 P 1 、 P 2 、 P 3 、 P 4 P_1、P_2、P_3、P_4 P1?、P2?、P3?、P4?
1、定义优化变量：
x = [ l 1 l 2 l 3 l 4 l 1 ′ l 2 ′ l 3 ′ l 4 ′ l 1 ′ ′ l 2 ′ ′ l 3 ′ ′ l 4 ′ ′ ] x=\begin{bmatrix} l_1\\ l_2\\ l_3\\ l_4\\ l_1^{'}\\ l_2^{'}\\ l_3^{'}\\ l_4^{'}\\ l_1^{''}\\ l_2^{''}\\ l_3^{''}\\ l_4^{''} \end{bmatrix} x= ?l1?l2?l3?l4?l1′?l2′?l3′?l4′?l1′′?l2′′?l3′′?l4′′?? ?
2、Cost function设计
在这里插入图片描述
在这里插入图片描述
3、约束的设计
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

文章来源:https://blog.csdn.net/BigDavid123/article/details/135294799
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章