轻松搞懂递归算法

1、递归函数

????????要使用一款工具之前必须先知道这工具是什么。本节将分语法角度和逻辑角度带大家了解递归。

1.1、递归函数的定义

????????函数内部调用自己的函数称为递归函数，这点大家应该早有了解。那什么是递归？

????????递归这个词需要拆分成递和归来理解。递是传参，归则是返回，一切函数在调用时必然经过这两个步骤。在递归函数中，由于调用自身的属性，传参过程和返回过程都是连续的。此外，递归函数内部必须设定结束递归的条件，否则造成死递归，最终结果将导致栈溢出（栈溢出的原因参照这篇的开头部分：函数栈帧简述）。

1.2、递归思想

? ? ? ? 递归的核心思想便是问题拆解。如果一个问题能一层层拆解，拆解之后的小问题仍与大问题有相同的结构以及相同的处理逻辑，那么可以考虑使用递归。有点类似剥洋葱，不论洋葱剥了几层，剩下的部分仍然与完整的洋葱有一样的结构和一样的属性。而且，无论剥了几层皮，再剥下一层皮与剥第一层皮的过程没有任何区别。

1.3、递归过程

? ? ? ? 用下列常见的递归函数结构演示递归流程。

void Recursive(int arg)
{
    /*......*/
    if(conditions) return;
    Recursive(arg);
    /*......*/
}

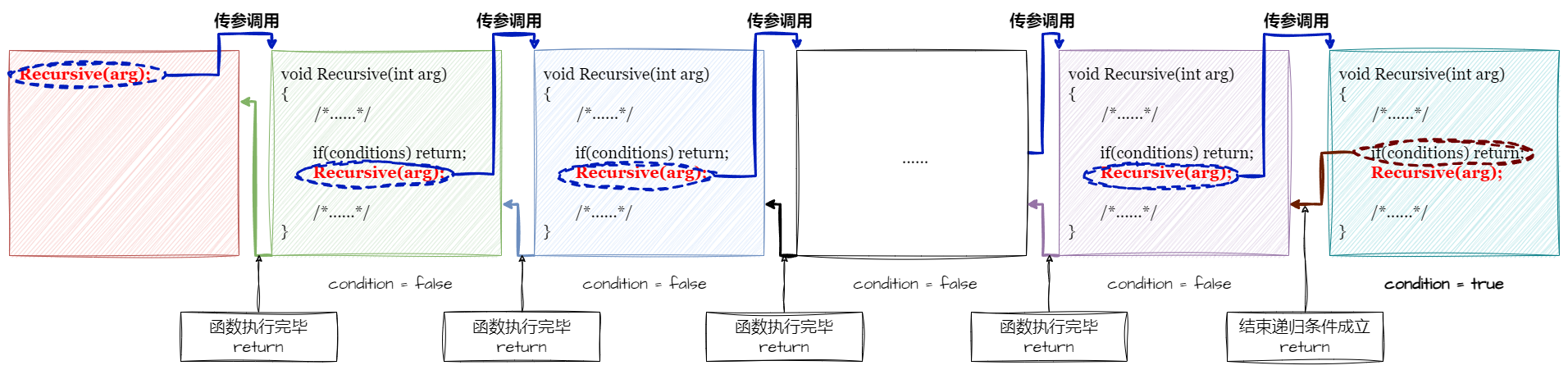
? ? ? ? 可见，递归函数内部调用自身和函数内部调用其他函数，二者并没有本质区别。每一层递归函数的自我调用都会创建一个新的栈帧。在内存层面，上一级函数和下一级函数处于不同的栈帧空间，所以这里可以理解成递归只是调用了一个同名函数，并将自身形参加以处理（也可以不处理）后传参于该同名函数。

2、递归与循环

2.1、功能及流程对比

? ? ? ? 先上代码：

void RecursivePrint(int num, int end, int step)
{
    if(num < end)
    {
        printf("%d ", num);
        num += step;
        RecursivePrint(num, end, step);
    }
}

int main()
{
    int num = 0;
    int end = 10;
    int step = 1;
    
    printf("递归：");
    RecursivePrint(num, end, step);

    printf("\n循环：");
    for(num = 0; num < end; num += step)
    {
        printf("%d ", num);
    }

    return 0;
}

? ? ? ? 运行结果显而易见，都是在屏幕上输出 0 到 9 。接下来就这两种方式画个流程图。

? ? ? ? 递归：

????????循环：

? ? ? ? 仔细观察发现，简单的递归不过是将每一次循环过程拆分开来，逻辑上完全一致。而且从上述两张图分析这两种方式的空间复杂度和时间复杂度。递归和循环的时间复杂度都是 O(N) ，但是在空间复杂度上，循环是 O(1) ，递归由于需要开辟栈帧空间，空间复杂度也处于 O(N) 级别。因此，只要循环可以轻松达到同样效果的情况下，尽量不要用递归。

? ? ? ? 此外，递归虽然在某些简单重复性的逻辑上与循环一致，但在稍复杂的重复性逻辑上，只有递归能做到。例如将上述递归函数稍作改动：

void RecursivePrint(int num, int end, int step)
{
    if(num < end)
    {
        printf("%d ", num);
        num += step;
        RecursivePrint(num, end, step);
        num += step;
        RecursivePrint(num, end, step);
    }
}

? ? ? ? ?要了解为什么这段代码实现的功能用循环语句做不到，必须先将上述递归的过程抽象理解为以前序的方式访问以下二叉树：

? ? ? ? 因为树的层级会随着 num 和 step 的变化而变化， end 的值对这棵树叶节点的未知也有决定性的作用。若用循环访问这棵树必须多重镶套循环才行，但 num、 step 和?end 的值是未知的，也就说明，循环镶套的层级是未知的。但循环语句是在敲代码时就确定了的，用循环处理只能做到特定重镶套，无法自由伸缩。因此循环做不到这个递归函数的功能。

2.2、思考方式对比

? ? ? ? 老样子，先看代码：

void ReadArr(int* arr, size_t size)
{
	if (!size) return;
	printf("%d ", arr[0]);
	ReadArr(arr + 1, size - 1);
}

int main()
{
	int arr[20] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 };
	for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
	ReadArr(arr, sizeof(arr) / sizeof(arr[0]));

	return 0;
}

? ? ? ? 运行结果毋庸置疑，都是遍历 arr?数组。但是，循环与递归在语义上是有明显区别的。

????????循环相当于一个指针指向数组，每打印一个数字后，指针向后挪动一位，再打印，再向后挪，直至遍历完整个数组。

? ? ? ? 递归则相当于打印数组的第一个元素，之后将数组的头元素截去，当作一个新数组，再将新数组的地址和元素个数进行传参，之后内部调用的递归函数同样是打印数组的第一个元素，再截去头元素，再传参，直到传入空数组。这是一种剥洋葱的思考方式。

3、创建递归函数

? ? ? ? 如何创建递归函数的重点在于什么情况下可以用递归处理。具体情况可以参照递归经典问题如青蛙跳台阶、汉诺塔、斐波那契数列等。这些内容网上一搜大把的资料，这里就不再说明。结论其实开头关于递归的思想中已经说得很明确了，如果是洋葱，则可以考虑递归（当然还得考虑空间复杂度的问题）。

? ? ? ? 其次得考虑清楚递归进行条件和结束条件，至于中间怎么处理数据并不那么重要。可以用下列格式辅助自己思考：

? ? ? ? 当然这个格式需要根据情况灵活变换。比如求斐波那契数列第 n 项（当然这里只是举例，千万不要用递归求斐波那契数列，自己算算时间复杂度）：

?? ? ? ? 但是 n 要么大于 2 要么小于等于 2 ，所以只要在 Feb 函数内指定递归条件或非递归条件其一即可。也可以多种条件对内部递归函数的调用进行不同传参，以及指定不同的非递归条件返回不同值。

? ? ? ? 之后将上面格式转换为代码是整个过程最简单的一步：

int Feb(int n)
{
    if(n <= 2) return 1;
    else return Feb(n - 1) + Feb(n - 2);
}

????????甚至：

int Feb(int n)
{
    return n <= 2 ? 1 : Feb(n - 1) + Feb(n - 2);
}

4、递归应用场景

? ? ? ? 递归最常用的场景在于动态规划和回溯。比如跟循环对比的最后一个代码用到的就是回溯的思想。树的遍历往往需要回溯的算法，在这里不展开说，以后有机会再单独出一篇回溯的文章。

? ? ? ? 至于动规，比如刚才斐波那契数列的递归代码，之所以说明不建议使用，是由于时间复杂度达到??量级。而时间复杂度之所以高，本质原因在于已经计算过的斐波那契数列项由于没有记录，需要重复运算。因此只需要将计算过的项记录，这能将时间复杂度降低为 O(N) 量级。

int Feb(int* febArr, int n)
{
    //未计算第n项的值则进行计算并记录
	if (!febArr[n])
	{
		febArr[n] = Feb(febArr, n - 1) + Feb(febArr, n - 2);
	}
    //返回第n项
	return febArr[n];
}

void GetFeb(int n)
{
    //外部是从1算起，但数组下标从0算起
	n--;
    //开辟空间
	int* febArr = (int*)calloc(n + 1, sizeof(int));
	if (!febArr) return;
    //初始化前2个数
	febArr[0] = 1;
	febArr[1] = 1;
    //递归
	Feb(febArr, n);
	printf("%d ", febArr[n]);

	free(febArr);
	febArr = NULL;
}

? ? ? ? 递归是个很强大的工具，但对内存资源的开销也是惊人的，如何通过算法和结构进行灵活搭配以节省时间和空间的开销才是递归最终需要探讨的问题。