机器学习实验4——CNN卷积神经网络分类Minst数据集

🧡🧡实验内容🧡🧡

基于手写minst数据集，完成关于卷积网络CNN的模型训练、测试与评估。

🧡🧡 原理🧡🧡

卷积层
通过使用一组可学习的滤波器（也称为卷积核）对输入图像进行滑动窗口卷积操作，这样可以提取出不同位置的局部特征，从而捕捉到图像的空间结构信息。
激活函数
在卷积层之后，通常会应用一个非线性激活函数，如 ReLU激活函数的作用是引入非线性，使得 CNN 能够学习更复杂的特征表达。
池化层
池化层用于降低特征图的空间尺寸，同时保留最显著的特征信息（类似于人眼观物，是根据物体的主要轮廓来判断物体是什么，而对一些小细节第一眼并没有那么关注）。常见的池化方式包括最大池化和平均池化，它们可以减少计算量，并增加模型的平移不变性。
全连接层
一般在 CNN 的最后几层，全连接层被用来将先前的卷积和池化层的输出与目标类别进行关联，每个神经元在该层中与前一层的所有神经元相连，通过学习权重参数来进行分类决策。
Softmax 函数
在最后一个全连接层之后，通常会应用 Softmax 函数来将神经网络的输出转换为概率分布，用于多类别分类问题的预测。
例如p=[0.2,0.3,0.5]，这表示分类为类别1、2、3的概率分别为0.2，0.3，0.5，因此预测分类结果为类别3.
最后通过反向传播算法，CNN 使用训练数据进行模型参数的优化，它通过最小化损失函数（如交叉熵）来调整网络权重，并使用梯度下降等优化算法进行迭代更新。

构建本实验的CNN网络：

• 5 x 5的卷积核，输入通道为1，输出通道为16：此时图像矩经过卷积核后尺寸变成24 x 24。
• 2 x 2 的最大池化层：此时图像大小缩短一半，变成 12 x 12，通道数不变；
• 再次经过 5 x 5 的卷积核，输入通道为16，输出通道为32：此时图像尺寸经过卷积核后变成8 *8。
• 再次经过 2 x 2 的最大池化层：此时图像大小缩短一半，变成4 x 4，通道数不变；
• 最后将图像整型变换成向量，输入到全连接层中：输入一共有4 x 4 x 32 = 512 个元素，输出为10.
  -

🧡🧡CNN实现分类Minst🧡🧡

代码

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.optim as optim
from torch import nn, optim
from time import time

# ======================准备数据集======================
batch_size = 64
transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,))
])
train_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=True,
                               download=True,
                               transform=transform)
train_loader = DataLoader(train_dataset,
                          shuffle=True,
                          batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist',
                              train=False,
                              download=True,
                              transform=transform)
test_loader = DataLoader(test_dataset,
                         shuffle=False,
                         batch_size=batch_size)


# ======================CNN net======================
class CNN_net(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(1, 16, kernel_size=5)  # 卷积1
        self.pooling1 = nn.MaxPool2d(2)  # 最大池化
        self.relu1 = nn.ReLU()  # 激活

        self.conv2 = nn.Conv2d(16, 32, kernel_size=5)
        self.pooling2 = nn.MaxPool2d(2)
        self.relu2 = nn.ReLU()

        self.fc = nn.Linear(512, 10)  # 全连接

    def forward(self, x):
        batch_size = x.size(0)
        x = self.conv1(x)
        x = self.pooling1(x)
        x = self.relu1(x)
        x = self.conv2(x)
        x = self.pooling2(x)
        x = self.relu2(x)
        x = x.view(batch_size, -1)
        x = self.fc(x)
        return x


model = CNN_net()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

# ====================== train ======================
def train(epoch):
    time0 = time()  # 记录下当前时间
    loss_list = []
    for e in range(epoch):
        running_loss = 0.0
        for images, labels in train_loader:
            outputs = model(images)  # 前向传播获取预测值
            loss = criterion(outputs, labels)  # 计算损失
            loss.backward()  # 进行反向传播
            optimizer.step()  # 更新权重
            optimizer.zero_grad()  # 清空梯度
            running_loss += loss.item()  # 累加损失
        # 一轮循环结束后打印本轮的损失函数
        print("Epoch {} - Training loss: {}".format(e, running_loss / len(train_loader)))
        loss_list.append(running_loss / len(train_loader))
    # 打印总的训练时间
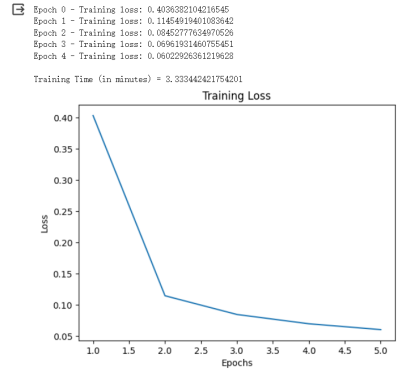
    print("\nTraining Time (in minutes) =", (time() - time0) / 60)

    # 绘制损失函数随训练轮数的变化图
    plt.plot(range(1, epoch + 1), loss_list)
    plt.xlabel('Epochs')
    plt.ylabel('Loss')
    plt.title('Training Loss')
    plt.show()

train(5)

# ====================== test ======================
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt


def test():
    model.eval()  # 将模型设置为评估模式
    correct = 0
    total = 0
    all_predicted = []
    all_labels = []
    with torch.no_grad():
        for images, labels in test_loader:
            outputs = model(images)
            _, predicted = torch.max(outputs.data, dim=1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()

            all_predicted.extend(predicted.tolist())
            all_labels.extend(labels.tolist())
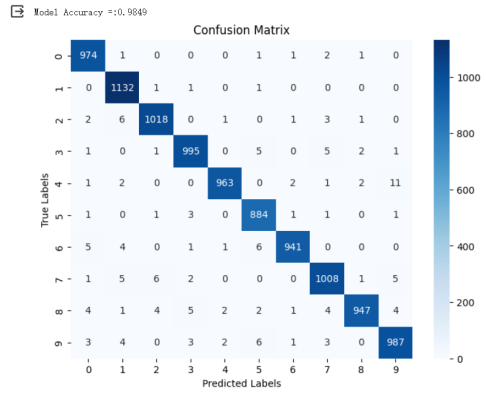
    print('Model Accuracy =:%.4f' % (correct / total))
    # 绘制混淆矩阵
    cm = confusion_matrix(all_labels, all_predicted)
    plt.figure(figsize=(8, 6))
    sns.heatmap(cm, annot=True, fmt=".0f", cmap="Blues")
    plt.xlabel("Predicted Labels")
    plt.ylabel("True Labels")
    plt.title("Confusion Matrix")
    plt.show()

test()

数据预处理：

加载数据集：
加载torch库中自带的minst数据集
转换数据：
先转为tensor变量（相当于直接除255归一化到值域为(0,1)）
然后根据std=0.5，mean=0.5，再将值域标准化到（-1，1）。
（做完实验后，上网了解发现minst最合适的的std和mean分别为0.1307, 0.3081，但是其实结果都差不多，准确率变化不大，因为数据集还是相对比较简单的）

设置基本参数：

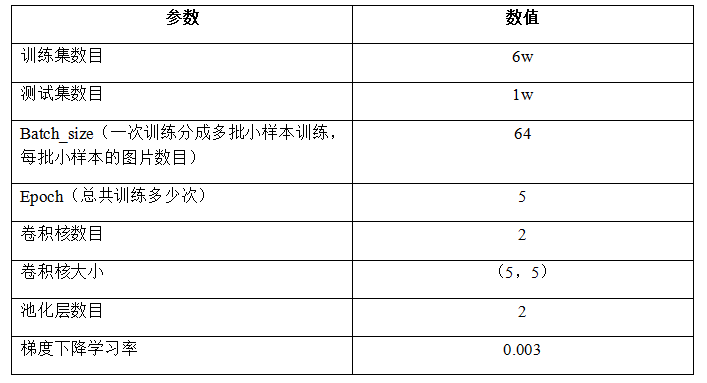
构建CNN神经网络：
同上述（1）中，已经构建完毕，这里不再赘述。
模型训练：

可见，虽然只经过5个epoch，但是花的时间为3.3min。
模型分类：

准确率达98.26%。