【LeetCode刷题笔记(3)】【Python】【最长连续序列】【中等】
文章目录
最长连续序列
最长连续序列
题目描述
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例
示例 1
- 输入:nums = [100,4,200,1,3,2]
- 输出:4
- 解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2
- 输入:nums = [0,3,7,2,5,8,4,6,0,1]
- 输出:9
提示
- 0 <= nums.length <= 105
- -109 <= nums[i] <= 109
解决方案
不要求序列元素在原数组中连续 ==> 我们可以对原数组【去重】并转换为【新数组】,然后只需要遍历一遍新数组即可查找出数字连续的最长序列。
解决方案1:【集合去重】+【遍历数组查找元素】
代码如下:
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
# 将列表转换为集合以去除重复元素,然后再次转换为列表
nums = list(set(nums))
# 初始化最长连续序列的长度为0
longest_len = 0
# 遍历新数组
for n in nums:
# 如果n-1已在数组中,那么当前n一定在遍历n-1时被当作连续的数而计数过,就一定存在longest_num(从n-1开始) = longest_num(从n开始) + 1, 因此这是无效计数
# 如果n-1不在数组中, 那么这是一次有效计数
if n - 1 not in nums:
# 初始化当前连续序列的长度为1
cur_len = 1
# 当n的后一个数在列表中时,继续增加当前连续序列的长度,并更新n的值
while n + 1 in nums:
cur_len += 1
n += 1
# 如果当前连续序列的长度大于最长连续序列的长度,则更新最长连续序列的长度
if cur_len > longest_len:
longest_len = cur_len
# 返回最长连续序列的长度
return longest_len
避免无效计数
理论上,我们可以将数组的每个数(比如n)都作为起点,通过依次查找n+1、n+2…是否存在于数组中来更新数字连续的最大长度。但这样会出现很多无效计数 —> 当已知n存在时,仍然以n+1作为起点,那么longest_num(从n开始) = longest_num(从n+1开始) + 1恒成立 ==>longest_num(从n开始) > longest_num(从n+1开始)恒成立。由于我们仅仅需要统计数字连续的最长序列长度,因此,从n
+1、n+2作为起点的统计都是无效统计。(这个思想在代码中已体现~)
方案1的可行性分析
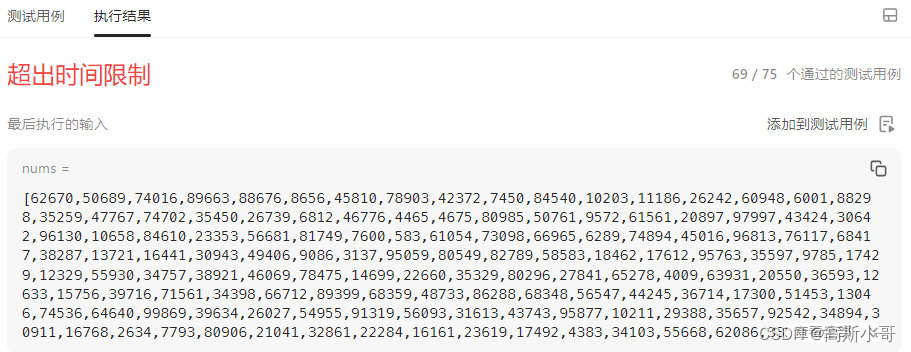
但根据题意要求,只能设计时间复杂度为 O(n) 的算法。遗憾的是,遍历数组 + 在数组中查找元素的时间复杂度是O(nlogn(遍历+二分查找) or n2(遍历+顺序查找)) > O(n) 。因此,【集合去重】+【遍历数组查找元素】尽管可以解决这个问题,但无法满足时间复杂度的要求。报错如下:
解决方案2:【集合去重】+ 【遍历集合查找元素】
问题1: 从时间复杂度分析可以看出,问题出在了【遍历数组查找元素】上。首先遍历是无法去掉的 ? 需要将查找元素的时间复杂度降为O(1),那么什么数据结构查找元素的时间复杂度是O(1)?
哈希表!!!
问题2:在Python中,哪些基于哈希表的数据结构适合存储数组元素呢?
集合set!!!更有趣的是,集合把去重的工作也包揽了~
想清楚这两个关键问题,代码也就简单了:
class Solution:
def longestConsecutive(self, nums: List[int]) -> int:
# 将输入的列表转换为集合,以便快速查找元素
nums_set = set(nums)
# 初始化最长连续序列的长度为0
longest_len = 0
# 遍历集合中的每个元素
for n in nums_set:
# 如果n的前一个数在集合中,则跳过当前元素
if n - 1 in nums_set:
continue
# 初始化当前连续序列的长度为1
cur_len = 1
# 当n的后一个数在集合中时,增加当前连续序列的长度,并更新n的值
while n + 1 in nums_set:
cur_len += 1
n += 1
# 如果当前连续序列的长度大于最长连续序列的长度,则更新最长连续序列的长度
if cur_len > longest_len:
longest_len = cur_len
# 返回最长连续序列的长度
return longest_len
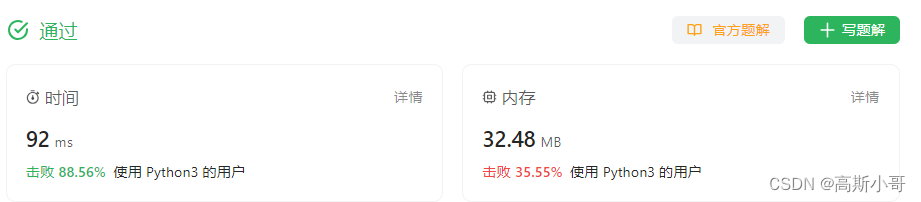
运行结果
复杂度分析
-
时间复杂度:O(N),其中 N 是数组
nums元素的数量。- 需要将数组转成集合 ===> O(N)
- 需要遍历集合,极端情况下集合元素个数和数组nums元素个数相等 ==> O(N)
- 每次遍历需要查找集合中的元素 ===> O(1)
- 总时间复杂度 ===> O(N)
-
空间复杂度:O(N)
- 创建了一个集合
nums_set来存储元素个数为N的数组nums===> O(N)
- 创建了一个集合
结束语
- 亲爱的读者,感谢您花时间阅读我们的博客。我们非常重视您的反馈和意见,因此在这里鼓励您对我们的博客进行评论。
- 您的建议和看法对我们来说非常重要,这有助于我们更好地了解您的需求,并提供更高质量的内容和服务。
- 无论您是喜欢我们的博客还是对其有任何疑问或建议,我们都非常期待您的留言。让我们一起互动,共同进步!谢谢您的支持和参与!
- 我会坚持不懈地创作,并持续优化博文质量,为您提供更好的阅读体验。
- 谢谢您的阅读!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 初识C语言(C语言笔记,简述C语言的部分知识点)
- Linux下安装jdk
- ai写论文大纲的软件有哪些?介绍5个简单好用的软件
- 深入云原生—基于KubeWharf深度剖析-以公司实际应用场景为例深度解读
- 这里分享一个对windows系统有用的免费软件app附送链接
- 【开题报告】基于SpringBoot的手机在线销售商城设计与实现
- 半导体:Gem/Secs基本协议库的开发(5)
- NET Core使用SkiaSharp生成二维码
- B树和B+树的区别
- 存储RAID技术详解