LeetCode 94. 二叉树的中序遍历
发布时间:2024年01月10日
94. 二叉树的中序遍历
给定一个二叉树的根节点?root?,返回?它的?中序?遍历?。
示例 1:
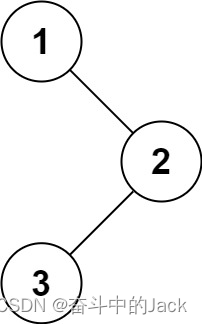
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
- 树中节点数目在范围?[0, 100]?内
- -100 <= Node.val <= 100
进阶:?递归算法很简单,你可以通过迭代算法完成吗?
解法思路:
1、递归(Recursion)
2、迭代维护栈(Iterator)
3、Morris 中序遍历(了解一下)
Morris 遍历算法是另一种遍历二叉树的方法,它能将非递归的中序遍历空间复杂度降为 O(1)
Morris 遍历算法步骤(假设当前遍历到的节点为 x):
- 若 x 无左孩子
- x 加入结果
- x = x.right
- 若 x 有左孩子,找 x 左子树的最右边的节点 predecessor
- predecessor 右孩子为空,右孩子指向x,x = x.left
- predecessor 右孩子不为空,x 加入结果,x = x.right
- 重复上述步骤,直到访问完整棵树
法一:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
// Recursion
// Time: O(n)
// Space: O(n)
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
private void inorder(TreeNode root, List<Integer> res) {
if (root == null) return;
inorder(root.left, res);
res.add(root.val);
inorder(root.right, res);
}
}
法二:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
// Iterator
// Time: O(n)
// Space: O(n)
List<Integer> res = new ArrayList<>();
Deque<TreeNode> stack = new ArrayDeque<>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.addLast(root);
root = root.left;
}
root = stack.removeLast();
res.add(root.val);
root = root.right;
}
return res;
}
}
法三:?
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
// Morris
// Time: O(n)
// Space: O(1)
// Morris 遍历算法步骤(假设当前遍历到的节点为 x):
// 若 x 无左孩子
// x 加入结果
// x = x.right
// 若 x 有左孩子,找 x 左子树的最右边的节点 predecessor
// predecessor 右孩子为空,右孩子指向x,x = x.left
// predecessor 右孩子不为空,x 加入结果,x = x.right
// 重复上述步骤,直到访问完整棵树
List<Integer> res = new ArrayList<>();
TreeNode predecessor = null;
while (root != null) {
if (root.left != null) {
// predecessor 节点就是当前 root 节点向左走一步,然后一直向右走至无法走为止
predecessor = root.left;
while (predecessor.right != null && predecessor.right != root) {
predecessor = predecessor.right;
}
// 让 predecessor 的右指针指向 root,继续遍历左子树
if (predecessor.right == null) {
predecessor.right = root;
root = root.left;
} else { // 说明左子树已经访问完了,需要断开链接
res.add(root.val);
predecessor.right = null;
root = root.right;
}
} else {
res.add(root.val);
root = root.right;
}
}
return res;
}
}
?
文章来源:https://blog.csdn.net/qq_38304915/article/details/135499498
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 图论 | 网络流的基本概念
- java项目之基于协同过滤算法的图书推荐系统(ssm)
- JavaScript读写T5557卡源码
- java网络文件地址url的转换为MultipartFile文件流
- SQL-- 在一个分组内随机抽取几条数据
- window.open 跳转http自动重定向https问题
- 程序员必备的面试技巧
- Linux stm32串口下载程序
- 【Docker】Dockerfile 指令详解
- electron桌面应用开发——快速入门教程