三角形较大边所对的角较大

发布时间：2024年01月19日

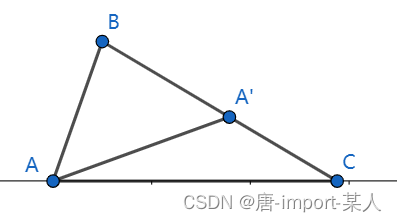
在这里插入图片描述

设△ABC中BC>AB
$在 BC 上做 B A 同长度的 B A^{'}, 链接 A ’ A$
$∵ B A = B A ’$
$∴ ∠ B A A^{'} = ∠ B A^{'} A$
$∵ ∠ B A A^{'} 在 ∠ A 内$
$∴ ∠ B A^{'} A < ∠ A$
$∵ ∠ B A ’ A > ∠ C$ 原理
$∴ ∠ A > ∠ B A^{'} A > ∠ C$

文章来源:https://blog.csdn.net/tyh751734196/article/details/135689620
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！