洛谷 NOIP2014普及组 比例简化 + 洛谷 NOIP2015普及组 扫雷游戏
发布时间:2023年12月23日
先看第一道题比例简化:
题干:

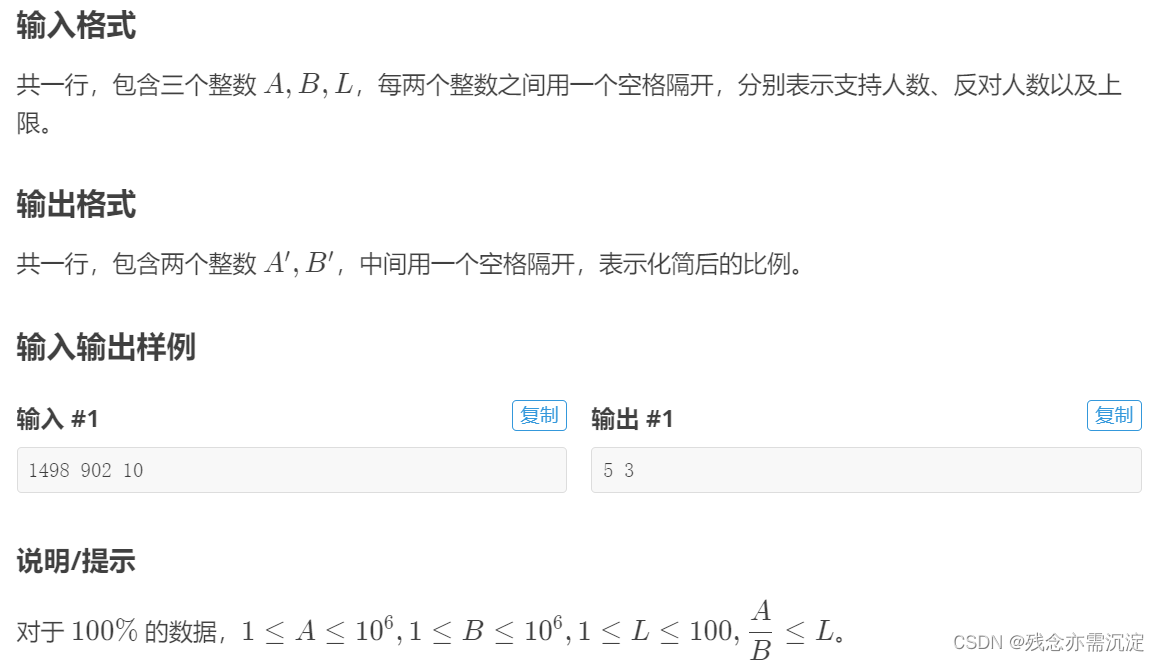
输入输出样例以及样例范围:
 ?
?
其实不难看出这一道题目的样例范围并不大,所以其实我们可以用暴力枚举的方式进行解答,虽然暴力枚举在很多题目并不值得提倡,不过不得不承认它是一种更容易让人理解的方法。
对于这一道题,要求新的A',B'的比值要大于等于A/B并且二者之差尽可能小,同时新的A',B'互质而且不能大于L。其实思路很明确了,我们只需要二重循环,分别从1到L进行枚举,通过不断的更新答案,就会得到最后的结果,另外我们需要写一个判断两个数字是否互质,直接上代码:
#include<iostream>
#include<cmath>
using namespace std;
int A,B,L;
bool coprime(int a,int b){
for(int d=2;d<=a;d++){
if(!a%d && !b%d)
return false;
}
return true;
}
int main(){
cin>>A>>B>>L;
double ans=1<<23;
int ansA=-1,ansB=-1;
for(int a=1;a<=L;a++){
for(int b=1;b<=L;b++)
{
//a,b互质且a/b>=A/B
if(coprime(a,b) && (double)a/b>=(double)A/B){
double tmp=1.0*a/b-1.0*A/B;
if(tmp<ans){
ans=tmp;
ansA=a;
ansB=b;
}
}
}
}
cout<<ansA<<' '<<ansB<<endl;
return 0;
}这一道题目的难度并不大,想道两重循环和中间变量tmp来更新ans即可。
第二道题目,扫雷游戏:
先看题目:
 ?接下来看输入输出样例以及数据范围:
?接下来看输入输出样例以及数据范围:

这道题目就是一道简单的模拟题,主要是需要考虑的是再计算每一个格子周围的地雷数目时,我们通过怎样的代码来计算,更为佳,下面是我的代码:
#include<bits/stdc++.h>
using namespace std;
int n,m;
char a[110][110];
int ans[110][110];
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
scanf("%s",a[i]);
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(a[i][j]=='*'){
ans[i][j]=-1;
continue;
}
for(int dx=-1;dx<=1;dx++){
for(int dy=-1;dy<=1;dy++){
if(dx==0 && dy==0) continue;
int x=i+dx,y=j+dy;
if(x>=0 && x<n && y>=0 && y<m){
if(a[x][y]=='*')
ans[i][j]++;
}
}
}
}
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(ans[i][j]==-1) printf("*");
else printf("%d",ans[i][j]);
}
printf("\n");
}
return 0;
}我用dx,dy从-1开始,1为止,来枚举每一个数字的周围九个格子,当然了,当周围的某个格子是空白的时候需要特判,所有我加了if作为特判条件,这样就能轻松的完成本题了。
文章来源:https://blog.csdn.net/2301_80050923/article/details/135159477
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章