「优选算法刷题」:在排序数组中查找元素的第一个和最后个位置

一、题目

给你一个按照非递减顺序排列的整数数组?nums，和一个目标值?target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值?target，返回?[-1, -1]。

你必须设计并实现时间复杂度为?O(log n)?的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例?2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

二、思路解析

二分查找，它很简单，但也很容易写出死循环。不过，不必过多恐惧，只要多做练习，他就会是最简单的查找算法！

我们来看这道题，主要分为 2 部分：查找区间的左端点 和 右端点。

1）查找区间左端点

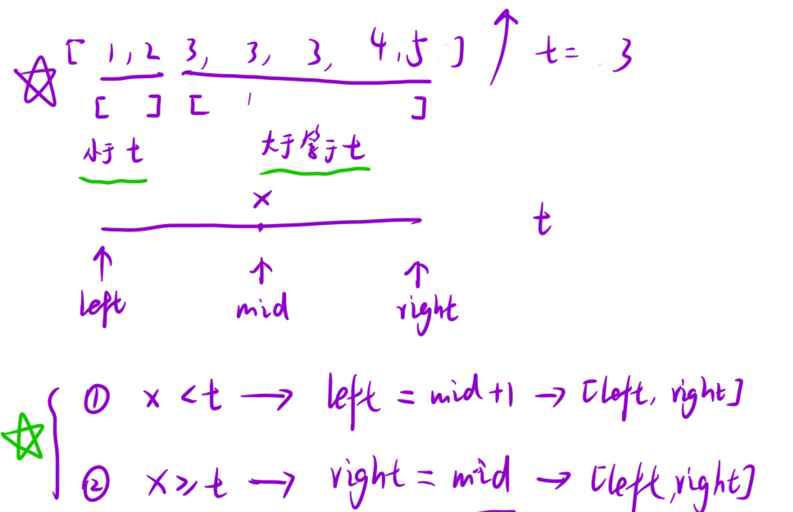
左边界划分的两个区间的特点：

? 左边区间 [left, resLeft - 1] 都是?于 x 的；
? 右边区间（包括左边界） [resLeft, right] 都是?于等于 x 的；

因此，关于 mid 的落点，我们可以分为下?两种情况：

? 当我们的 mid 落在 [left, resLeft - 1] 区间的时候，也就是 arr[mid] <target 。说明 [left, mid] 都是可以舍去的，此时更新 left 到 mid + 1 的位置，继续在 [mid + 1, right] 上寻找左边界；

? 当 mid 落在 [resLeft， right] 的区间的时候，也就是 arr[mid] >= target 。说明 [mid + 1, right] （因为 mid 可能是最终结果，不能舍去）是可以舍去的，此时更新 right 到 mid 的位置，继续在 [left, mid] 上寻找左边界；

注意：这?找中间元素需要向下取整，即 mid = left + ( right - left ) / 2 ，而不是?mid = left + ( right - left + 1?) / 2 。

因为后续移动左右指针的时候：
? 左指针： left = mid + 1 ，是会向后移动的，因此区间是会缩?的；
? 右指针： right = mid ，可能会原地踏步（?如：如果向上取整的话，如果剩下 1,2 两个元
素， left == 1 ， right == 2 ， mid == 2 。更新区间之后， left，right，mid 的
值没有改变，就会陷?死循环）。
因此?定要注意，当 right = mid 的时候，要向下取整。

2）查找区间右端点

我们先? resRight 表?右边界；

这时可以注意到右边界的特点：

????????? 左边区间 （包括右边界） [left, resRight] 都是?于等于 x 的；
????????? 右边区间 [resRight+ 1, right] 都是?于 x 的；

因此，关于 mid 的落点，我们可以分为下?两种情况：

? 当我们的 mid 落在 [left, resRight] 区间的时候，说明 [left, mid - 1]（ mid 不可以舍去，因为有可能是最终结果） 都是可以舍去的，此时更新 left 到 mid的位置；
? 当?mid 落在 [resRight+ 1, right] 的区间的时候，说明?[mid, right] 内的元素是可以舍去的，此时更新?right 到?mid - 1 的位置；

? 由此，就可以通过?分，来快速寻找右边界；
注意：这?找中间元素需要向上取整「?mid = left + ( right - left + 1?) / 2」。

因为后续移动左右指针的时候：
? 左指针： left = mid ，可能会原地踏步（比如：如果向下取整的话，如果剩下?1,2 两个元
素， left == 1， right == 2，mid == 1 。更新区间之后， left，right，mid ?的值
没有改变，就会陷?死循环）。
? 右指针： right = mid - 1 ，是会向前移动的，因此区间是会缩小的；
因此?定要注意，当? right = mid ?的时候，要向下取整。

三、完整代码

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int ret[] = new int[2];
        ret[0] = ret[1] = -1;

        // 处理边界情况
        if(nums.length == 0){
            return ret;
            }

        // 1. ?分左端点    
        int left = 0;
        int right = nums.length - 1;
        while(left < right){
            int mid = left + (right - left) / 2;
            if(nums[mid] < target){
                left = mid + 1; 
            }else{
                right = mid;
            }
        }

        // 判断是否有结果
        if(nums[left] != target){
            return ret;
        }else{
            ret[0] = left;
        }

        // 2. ?分右端点
        left = 0;
        right = nums.length - 1;
        while(left < right){
            int mid = left + (right - left + 1) / 2;
            if(nums[mid] <= target){
                left = mid;
            }else{
                right = mid - 1;
            }
        }
        ret[1] = right;
        return ret ;
    }
}

以上就是本篇博客的全部内容啦，如有不足之处，还请各位指出，期待能和各位一起进步！