力扣LCR 165. 解密数字(动态规划)
Problem: LCR 165. 解密数字
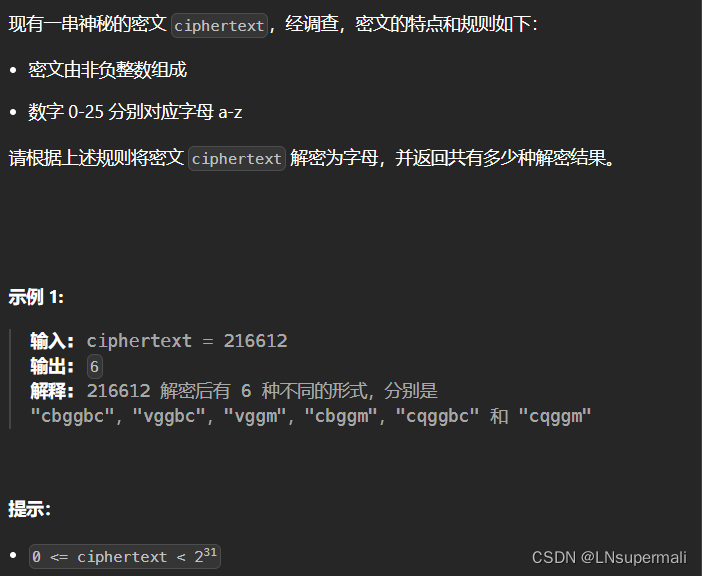
题目描述:
思路
1.每个阶段从1个或者2个数字翻译
2.int dpn + 1 dp[i]表示长度位i的数字序列有多少种翻译方法,到达i这个状态,那上一步只有可能是选择了1个或者两个数字翻译,也就是从状态i - 1, i - 2转换过来,dp[i]的值也有dp[i - 1]和dp[i - 2]推到过来;
3.dp[i] = dp[i - 1] + dp[i - 2];(前提是2个数字不超过25)
解题方法
1.将给定的数字ciphertext存入数组中;
2.编写判断当前两个数字位是否在解密的范围内(函数名为isValid(int a, int b))
3.初始化dp[0] = 1;再从dp数组索引为1的位置开始执行动态转移方程:执行过程中先令dp[i] = dp[i - 1],再判断当前数字位的前两位是否合法(调用编写的isValid函数)
4.返回dp[n]
复杂度
时间复杂度:
O ( n ) O(n) O(n);其中 n n n为给定十进制整形数ciphertext的数字位长度;
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {
/**
* Get all decryption results(Dynamic programming)
* int ciphertext: Given number
*/
public:
int crackNumber(int ciphertext) {
if (ciphertext <= 9) {
return 1;
}
//Adds the given decimal number to the array
vector<int> digitList;
while (ciphertext != 0) {
digitList.push_back(ciphertext % 10);
ciphertext /= 10;
}
int n = digitList.size();
int *digits = new int[n];
for (int i = 0; i < n; ++i) {
digits[i] = digitList.at(n - i - 1);
}
//Represents how many ways to translate a sequence of numbers of length i
int *dp = new int[n + 1];
dp[0] = 1;
for (int i = 1; i <= n; ++i) {
dp[i] = dp[i - 1];
if (i - 2 >= 0 && isValid(digits[i - 2], digits[i - 1])) {
dp[i] += dp[i - 2];
}
}
return dp[n];
}
/**
* Determines whether the current digit can be deduced from the previous two digits
* int a: The first two digits of the current digit
* int b: The first digits of current digit
* return: bool
*/
private:
bool isValid(int a, int b) {
if (a == 1) {
return true;
}
if (a == 2 && b >= 0 && b <= 5) {
return true;
}
return false;
}
};
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 监控易:依托强大日志管理的全方位运维解决方案
- 百度CTO王海峰:文心一言用户规模破1亿
- Flink-容错机制
- 【Linux】linux踢出远程登录用户命令
- django mysql in 有序返回
- 安徽省暨合肥市“希望工程·梦想计划”小盖茨机器人捐赠启动仪式举行
- MySQL存储过程、创建、调用、查看、删除、存储过程与函数的额区别、缺陷等、存储过程写分页等
- Dude Suite Web 渗透测试工具
- Kafka集群部署
- 计算机基础面试题 |13.精选计算机基础面试题