HNU-算法设计与分析-实验4
算法设计与分析
实验4
计科210X 甘晴void 202108010XXX

目录
文章目录
1 回溯算法求解0-1背包问题
问题重述
一共有N件物品,第i(i从0开始)件物品的重量为weight[i],价值为value[i]。在总重量不超过背包承载上限maxw的情况下,求能够装入背包的最大价值是多少?并要求输出选取的物品编号。
(要求使用回溯法求解)
想法
使用回溯法。构造解空间树,从第0层到第n-1层,每层表示对于背包内某个物品的“取”或“不取”。第n层为答案层,在第n层进行判定结果是否是想要的(即能不能获得更优的解),若是就做出相应的处理。
这是一个万能的解空间树图,借来用用。
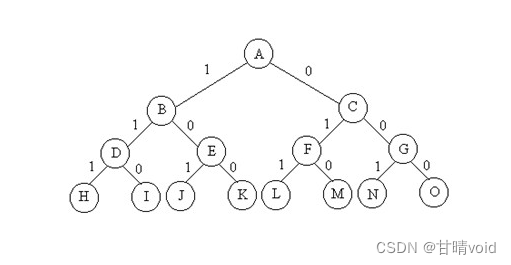
剪枝想法:
(1)如果在第n层之前,就出现了总和大于的maxw情况,那么此时已经超重了。之后无论是否取,都不可能再得到总和小于maxw的结果了。这种情况以及它的子树直接删去即可。
(2)如果在第n层之前,目前已有的价值,即使加上剩余可取的最大价值,也不能达到已经达到的bestv,那么之后即使全部取也不能达到bestv了。这种情况及它的子树直接删去即可。
剪枝代码可以删去,不影响结果,但会降低效率。
代码
// -*- coding:utf-8 -*-
// File : 01背包问题(回溯).cpp
// Time : 2023/12/14
// Author : wolf
#include <iostream>
using namespace std;
int w[5000];
int v[5000];
bool flag[5000];
bool ans[5000];
int now_w = 0, now_v = 0;
int n, maxw, bestv = 0;
int rest_v;
void backtrace(int depth)
{
if (depth == n) // 到达第n层:答案
{
if (now_v > bestv && now_w <= maxw) // 答案是需要打印的
{
bestv = now_v;
for (int i = 0; i < n; i++)
{
ans[i] = flag[i];
}
}
return;
}
if (depth < n && now_w > maxw)
return; // 剪枝:此时背包已经过重
if (now_v + rest_v <= bestv)
return; // 剪枝:此时剩余价值即使全部拾取也无法达到最大价值
rest_v -= v[depth];
// 取这个物品
now_v += v[depth];
now_w += w[depth];
flag[depth] = 1;
backtrace(depth + 1);
now_v -= v[depth];
now_w -= w[depth];
flag[depth] = 0;
// 不取这个物品
backtrace(depth + 1);
rest_v += v[depth];
return;
}
int main()
{
cin >> maxw >> n;
for (int i = 0; i < n; i++)
{
cin >> w[i] >> v[i];
ans[i] = 0;
flag[i] = 0;
rest_v += v[i];
}
backtrace(0);
// for (int i = 0; i < n; i++)
//{
// if (ans[i])
// cout << i << " ";
// }
// cout << endl;
// cout << "bestv=" << bestv << endl;
cout << bestv << endl;
return 0;
}
验证
洛谷P1048(https://www.luogu.com.cn/problem/P1048)
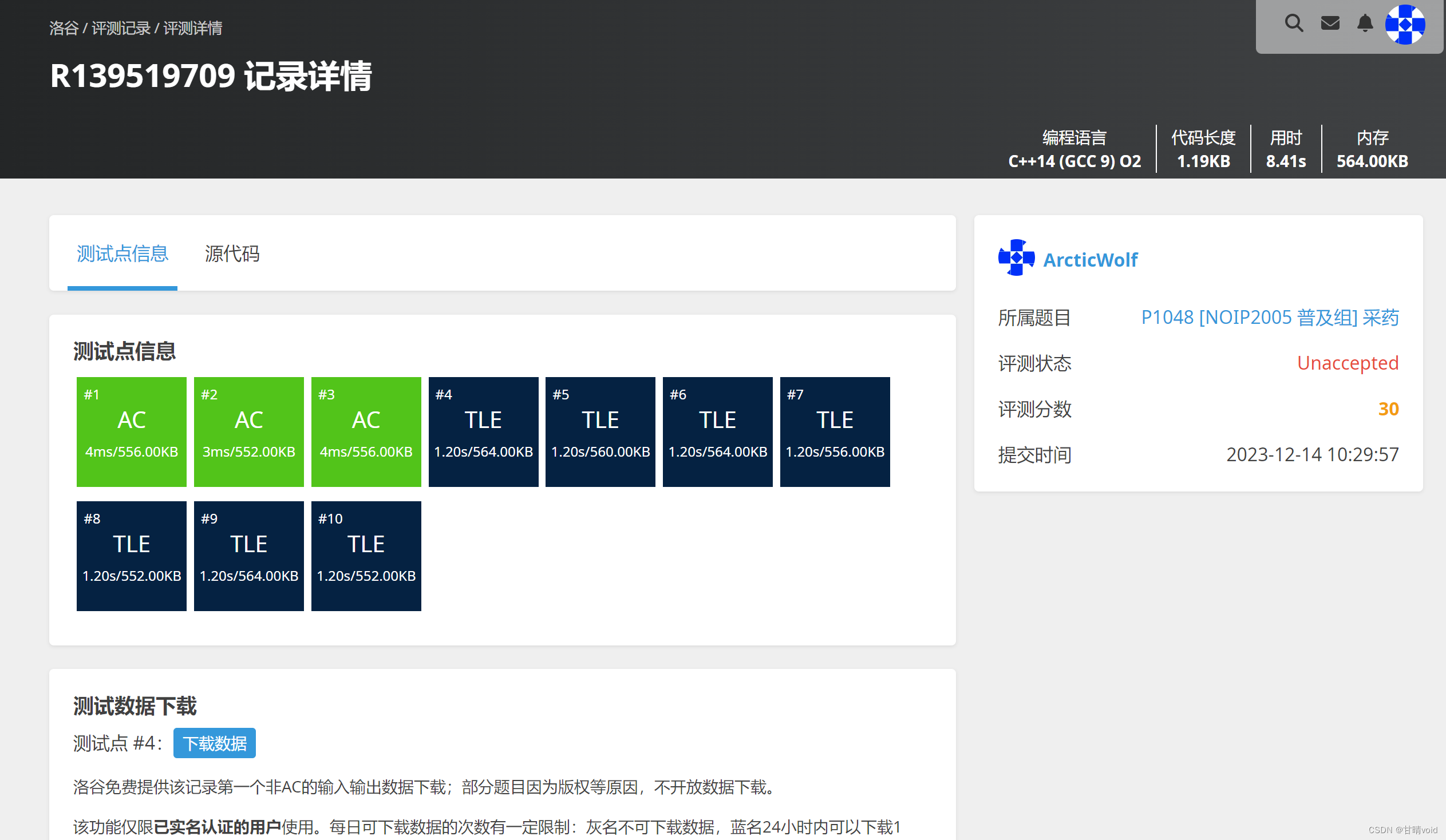
回溯法解决背包问题的O(2n)还是从数量级上显著不如动态规划的O(n2)。
故在数据量很大的时候,不能通过测评,显示超时。
所以01背包问题还是得用动态规划解,本题只是练习一下回溯法。
算法分析
时间复杂度O(2^n),解空间树是子集树
空间复杂度O(n),递归深度是n
2 回溯算法实现题5-4运动员最佳配对问题
问题重述
羽毛球队有男女运动员各n人。给定2个n×n矩阵P和Q。
P[i][j]是男运动员i的女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配对的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[i][j]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]×Q[i][j]。
设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
输入样例:
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1
输出样例:(输出竞赛优势的最大和)
52
案例解析:
10*2+4*5+4*3=52
即男1和女1,男3和女2,男2和女3
想法
最终的答案应该是对于每一个男运动员,都有一个女运动员与之配对。那么如果我们固定好男运动员,再给每一个男运动员配对女运动员,这样是等价的。
解向量x[1…n]表示第i个男运动员与第x[i]个女运动员配对,显然x[i]是不重复的。
解空间树是排列数(网上找了一张图如下)。
(图片来源于网络CSDN大佬)
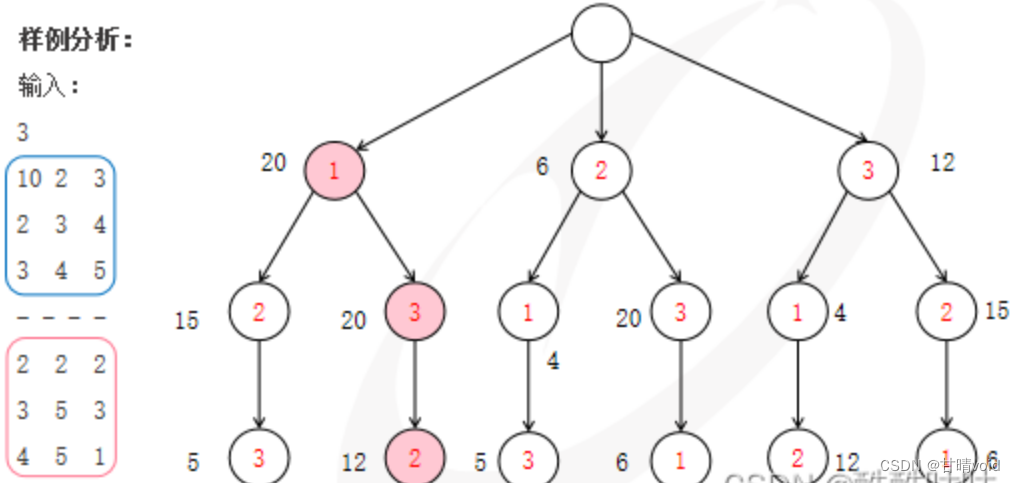
套用排列树的回溯法模板,思考剪枝思路。进行剪枝的时候要考虑代价问题,剪枝最好不要太复杂。这里的剪枝想法比较简单,基于贪心的思路。对于每个男运动员,我们都选和他产生价值最高的女运动员,不管该女运动员是否已经被选择了。这里显然有一个不等式,如果在当前状态下,后面每一个男运动员都选择能产生价值最大的女运动员的情况下,都不能达到最大的价值,那么往后就没有意义了,该状态的所有子状态需要被直接舍去。
本题对于数据处理上还有一些需要注意的地方。显然我们没必要每次都访问男女运动员单独的价值并做乘积运算,这样会产生大量的反复运算。分别读入各自价值之后,可以先求出r[i][j],即男运动员i和女运动员j能产生的价值。
然后对于贪心剪枝,我们没必要在回溯函数中反复计算剩下的男运动员和他们各自最优女运动员的价值和,这样也是冗余。仔细思考:这是可以预先在回溯函数之外处理好的。在计算r[i][j]之后,我们可以得到greedy_nowv[i],即男运动员i与其最佳女运动员的价值,即该男运动员在理想情况下可达到的最优价值。然后再使用类似前缀和的方式由后往前遍历,得到greedy_restv[i],表示第i个运动员以及之后的运动员在最理想的情况下所能达到的最大价值。
此外,函数中更新状态与恢复状态时,语句的先后不同一定要关注到,它的意义是不一样的。
swap(depth, i);
nowv += r[depth][girl_num[depth]];
backtrack(depth + 1);
nowv -= r[depth][girl_num[depth]];
swap(depth, i);
最后,引入girl_num[i]表示女运动员当前的排列序号(也就是解空间向量)。对r[i][j]的操作中,男运动员的一项用depth,女运动员的一项使用girl_num[i]。
代码
// -*- coding:utf-8 -*-
// File : P1159 运动员最佳匹配问题.cpp
// Time : 2023/12/20
// Author : wolf
#include <iostream>
using namespace std;
int p[20][20], q[20][20], r[20][20];
int greedy_maxnow[20], greedy_maxrest[20];
int girl_num[20];
int n, bestv = 0, nowv = 0;
void swap(int a, int b)
{
int temp;
temp = girl_num[a];
girl_num[a] = girl_num[b];
girl_num[b] = temp;
}
void backtrack(int depth)
{
if (depth == n) // 如果到达答案层
{
bestv = max(nowv, bestv);
}
else
{
if (nowv + greedy_maxrest[depth] <= bestv)
return; // 剪枝:若此层与后面所有贪心价值加起来都达不到最大值,直接退出
for (int i = depth; i < n; i++) // 排列树检索
{
swap(depth, i);
nowv += r[depth][girl_num[depth]];
backtrack(depth + 1);
nowv -= r[depth][girl_num[depth]];
swap(depth, i);
}
}
return;
}
int main()
{
cin >> n;
// 读入
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> p[i][j];
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cin >> q[i][j];
}
}
// 预处理
for (int i = 0; i < n; i++)
{
int maxnow = 0;
for (int j = 0; j < n; j++)
{
r[i][j] = p[i][j] * q[j][i]; // r[i][j]表示男i和女j配对的价值
maxnow = max(maxnow, r[i][j]);
}
greedy_maxnow[i] = maxnow; // greedy_maxnow[i]表示男i和最优的女配对的贪心价值
}
// 预处理:剪枝优化
for (int i = n - 1; i >= 0; i--)
{
if (i == n - 1)
greedy_maxrest[i] = greedy_maxnow[i]; // greedy_maxrest[i]表示剩下男i,男i+1,……,一直到男n-1都和最优的女配对的贪心价值
else
greedy_maxrest[i] = greedy_maxrest[i + 1] + greedy_maxnow[i];
}
for (int i = 0; i < n; i++)
girl_num[i] = i;
backtrack(0);
cout << bestv << endl;
return 0;
}
验证
洛谷P1559 运动员最佳匹配问题(https://www.luogu.com.cn/problem/P1559)
不使用剪枝,直接回溯:
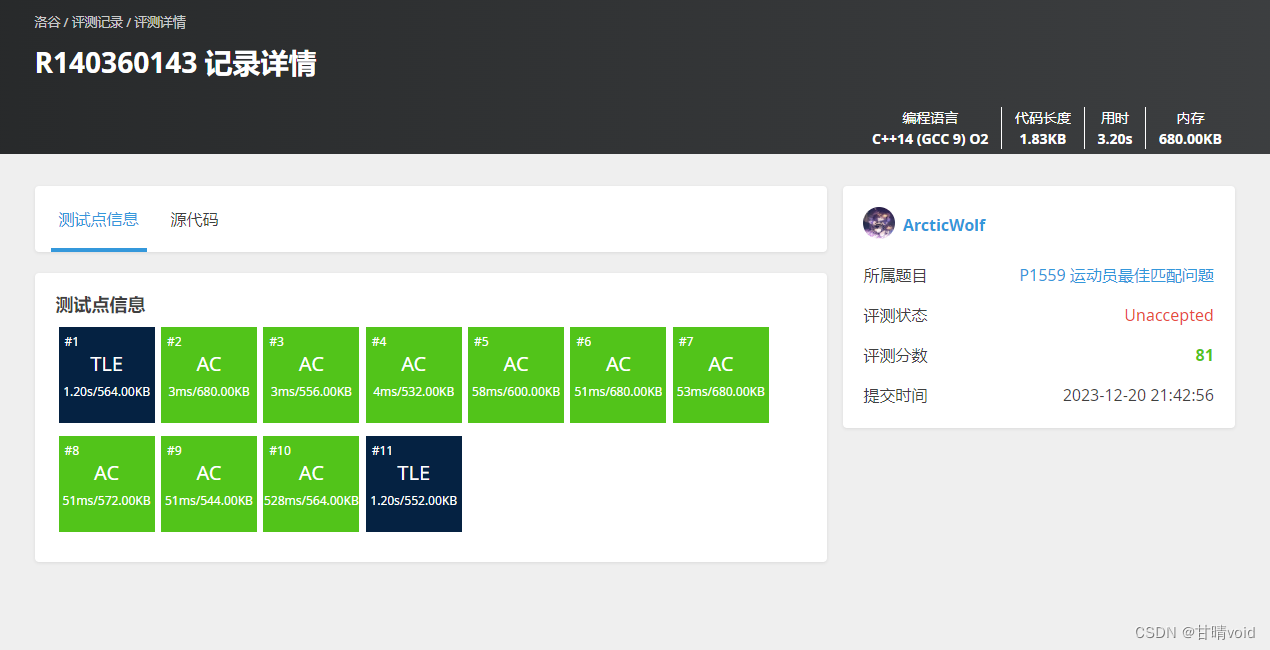
使用剪枝的回溯:
为什么被卡了一个数据点:
该题目的最好方法是用图论中的KM算法。时间复杂度比较如下:
- 暴力搜索 O(n!)【回溯法也算在这里】
- 费用流 O(n^2m)
- KM算法( DFS 实现增广) O(n^2m)
- KM算法( BFS实现增广) O(n^3)
因此,在一次新增数据点之后,回溯法就没法满分了。
算法分析
回溯法(解空间为排列树)
时间复杂度O(n!)
空间复杂度O(n^2)
3 分支限界法求解0-1背包问题
问题重述
一共有N件物品,第i(i从0开始)件物品的重量为weight[i],价值为value[i]。在总重量不超过背包承载上限maxw的情况下,求能够装入背包的最大价值是多少?并要求输出选取的物品编号。
(要求使用分支限界法求解)
想法
有参考学习:https://blog.csdn.net/LINZEYU666/article/details/119765116(但是这个的实现似乎有点问题)
这篇更好一点:https://blog.csdn.net/m0_57736712/article/details/124723032,有递归,分治,动态规划的各自实现和算法分析,性能比较。比较全面。
其它的CSDN,知乎等介绍的“分支限界法”有些跟书上的不一样,可能它们是理解错了。
书上说:分支限界法以最大效益优先的方式搜索问题的解空间树,在分支限界法扩展节点中,每个活结点只有一次机会成为扩展节点,一旦成为扩展节点,一次性产生其所有子节点,并舍弃不可行解(约束函数判定)与非最优解(上界函数判定)。
在这个基本思想下,有两种实现方法:队列式(FIFO)分支限界法和优先队列式分支限界法。
【队列实现】简单
想法
这个比较容易理解,就是一个队列,将每个节点产生的子节点全部放入队列中。按照先进先出的方式遍历,依次类推,直到所有节点遍历结束。实际上这就是一个广度优先搜索,逐层将解空间树搜索完。
(再用一下万能解空间树)
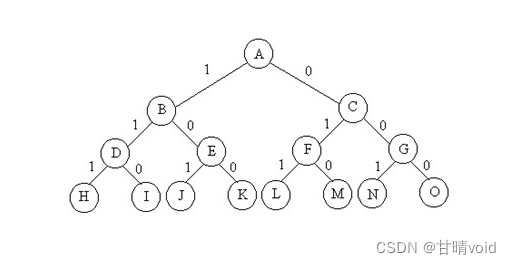
与回溯法一样,队列式的分支限界法遍历了解空间树的每一个子节点,直到最终的叶子节点层拿到答案。不同在于这次是逐行遍历的,而不是一次遍历到底。
与回溯法一样,队列式的分支限界法可以添加剪枝,以抛去明显不符合条件的子树,和明显不可能达到最优解的子树。
比起回溯法,这个对于解空间树的遍历更加“写实”一点,因为它真的创建了节点,然后真的用自己的方法在遍历节点,与抛去节点。
剪枝想法:
(1)约束函数:如果在第n层之前,就出现了总和大于的maxw情况,那么此时已经超重了。之后无论是否取,都不可能再得到总和小于maxw的结果了。这种情况以及它的子树直接删去即可。
(2)上界函数:如果在第n层之前,目前已有的价值,即使加上剩余可取的最大价值,也不能达到已经达到的bestv,那么之后即使全部取也不能达到bestv了。这种情况及它的子树直接删去即可。
代码1(粗略估算上界)
// -*- coding:utf-8 -*-
// File : 0-1背包(分支限界法)-队列.cpp
// Time : 2023/12/21
// Author : wolf
#include <iostream>
#include <queue>
using namespace std;
int w[5000];
int v[5000];
int rest_v[5000];
int maxw, n, bestv = 0;
// 节点:表示解空间树上的一个节点
struct Node
{
int now_w;
int now_v;
int depth;
Node(int _now_w, int _now_v, int _depth)
{
now_w = _now_w;
now_v = _now_v;
depth = _depth;
}
};
// 建立队列
queue<Node *> q;
void BFS()
{
Node *root = new Node(0, 0, -1);
q.push(root);
while (!q.empty())
{
Node *now = nullptr;
now = q.front();
q.pop();
if (now->depth == n) // 到达答案层
{
if (now->now_v > bestv && now->now_w < maxw)
{
bestv = now->now_v;
}
}
else
{
Node *fetch = new Node(now->now_w + w[now->depth + 1], now->now_v + v[now->depth + 1], now->depth + 1); // 取
Node *drop = new Node(now->now_w, now->now_v, now->depth + 1); // 不取
// 分支限界:剪枝:剪掉“不可行解”与“非最优解”
// 对于“取”,若取之后w已经大于maxw,这是不可行解,就舍去
if (fetch->now_w <= maxw)
q.push(fetch);
// 对于“不取”,可能产生非最优解,若到现在的价值加上剩余价值和都不可能达到最优,这是非最优解,舍去
if (drop->now_v + rest_v[drop->depth] > bestv)
q.push(drop);
}
delete (now);
}
}
int main()
{
cin >> maxw >> n;
for (int i = 0; i < n; i++)
{
cin >> w[i] >> v[i];
}
for (int i = n - 1; i >= 0; i--)
{
if (i == n - 1)
rest_v[i] = 0;
else
rest_v[i] = v[i + 1] + rest_v[i + 1];
} // 预先产生第i个物品之后所有物品和的总价值
BFS();
cout << bestv << endl;
return 0;
}
验证
洛谷P1048(https://www.luogu.com.cn/problem/P1048)
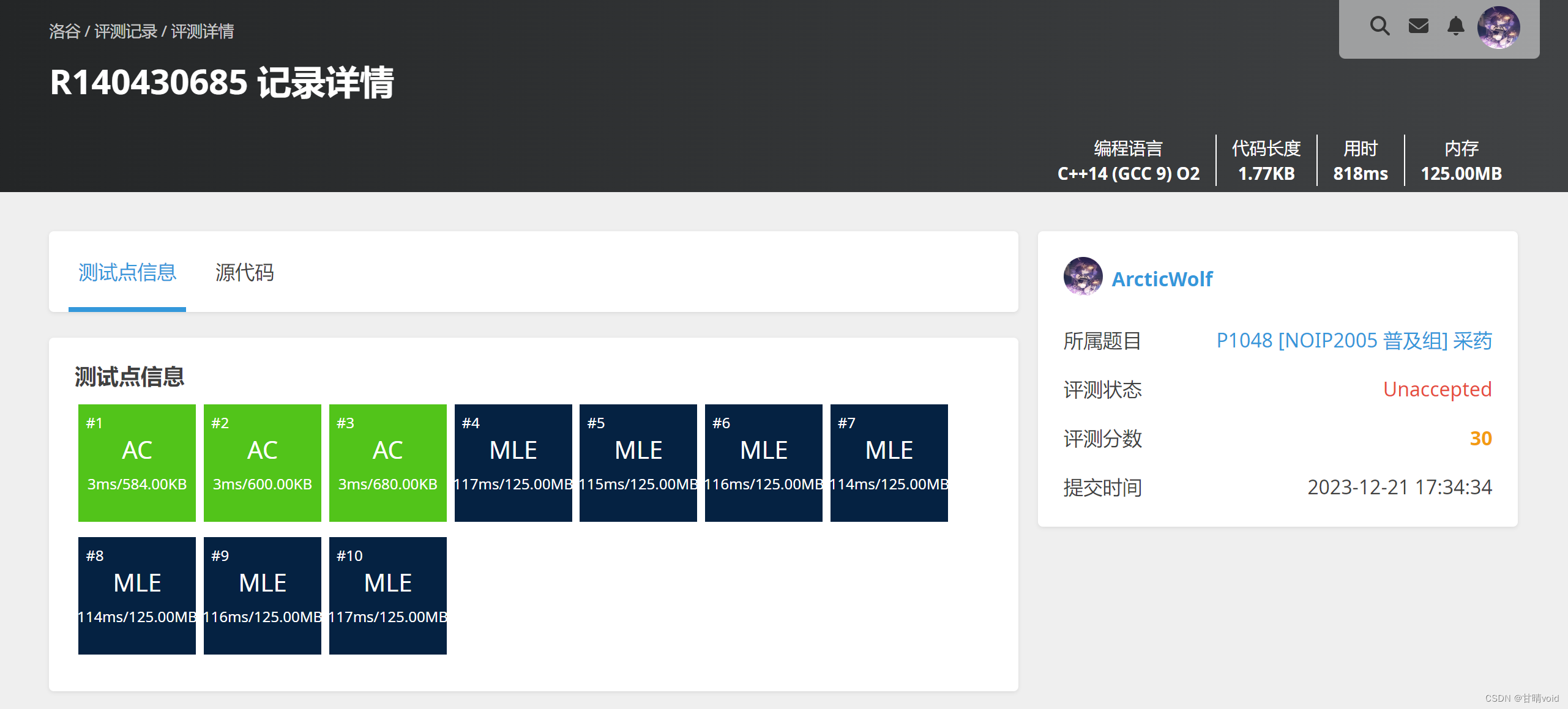
可见,将所有解空间树全部构造出来,对于较大的数据一定会超出空间。因为2^N大小的解空间树是没法存下的。
(MLE在后7个数据点上与回溯法的TLE相映成趣)
算法分析
时间复杂度:O(2^N)
空间复杂度:O(2^N)
【队列>优化】优化上界函数
想法
使用贪心的方法估算上界函数,会比直接把后面全部加起来要更加精确。前面一种简单加和有可能使物品超重,也就是说,上界函数达到了很大的价值,但是实际上有可能它已经超重了,但我们还浑然不知,这实际上太粗略了。如果我们能更精细地计算不超重的上界函数,虽然可能在计算上花的代价大了点,但是有可能会有更好的剪枝效果。
代码2(使用贪心估算上界)
// -*- coding:utf-8 -*-
// File : 0-1背包(分支限界法)-队列2.cpp
// Time : 2023/12/21
// Author : wolf
#include <algorithm>
#include <functional>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int rest_v[5000];
int maxw, n, bestv = 0;
// 商品:使用sort函数排序,商品价值与重量要带着走不方便,用结构体来保证
struct goods
{
int w;
int v;
double vpw;
} goods[5000];
// sort函数的排序依据:性价比较高的排在前面
bool cmp_goods(struct goods a, struct goods b)
{
return a.vpw > b.vpw;
}
// 节点:表示解空间树上的一个节点
struct Node
{
int now_w;
int now_v;
int depth;
Node(int _now_w, int _now_v, int _depth)
{
now_w = _now_w;
now_v = _now_v;
depth = _depth;
}
};
queue<Node *> q;
// 计算一个节点的总贪心价值
double get_greedy_v(int now_w, int now_v, int depth)
{
int wleft = maxw - now_w; // 剩余容量
int greedy_v = now_v; // 价值上界,函数返回值
// 以物品单位价值递减顺序排列
depth++;
while (depth < n && goods[depth].w <= wleft)
{
greedy_v += goods[depth].v;
wleft -= goods[depth].w;
depth++;
}
if (depth < n)
greedy_v += goods[depth].vpw * wleft;
return greedy_v;
}
void BFS()
{
Node *root = new Node(0, 0, -1);
q.push(root);
while (!q.empty())
{
Node *now = nullptr;
now = q.front();
q.pop();
// cout << "now:" << now->depth << endl;
if (now->depth == n) // 到达答案层
{
if (now->now_v > bestv)
bestv = now->now_v;
}
else
{
// Node(int _now_w, int _now_v, int _depth, double _rest_greedy_v)
int w = now->now_w;
int v = now->now_v;
int depth = now->depth;
// 分别计算已有的加上后面的贪心价值,这是这个节点的总贪心价值,也是优先队列的排序依据
// double fetch_greedy_v = get_greedy_v(w + goods[depth + 1].w, v + goods[depth + 1].v, depth + 1);
double drop_greedy_v = get_greedy_v(w, now->now_v, depth + 1);
if (w + goods[depth + 1].w <= maxw) // 剪枝:约束函数:排除不可行解(超重)(只需对左子树考虑)
{
if (v + goods[depth + 1].v > bestv)
{
bestv = v + goods[depth + 1].v; // 更新最优价值
}
Node *fetch = new Node(w + goods[depth + 1].w, v + goods[depth + 1].v, depth + 1);
q.push(fetch); // 取
}
if (drop_greedy_v > bestv) // 剪枝:约束函数:排除非最优解(只需对右子树考虑)
{
Node *drop = new Node(w, v, depth + 1);
q.push(drop); // 不取
}
delete (now); // 释放空间
// cout << "fetch:" << fetch_greedy_v << endl
// << "drop:" << drop_greedy_v << endl
// << endl;
}
}
}
int main()
{
cin >> maxw >> n;
for (int i = 0; i < n; i++)
{
cin >> goods[i].w >> goods[i].v;
goods[i].vpw = (double)(goods[i].v) / goods[i].w; // 计算性价比
}
sort(goods, goods + n, cmp_goods); // 预排序,使性价比较高的靠前
BFS();
cout << bestv << endl;
return 0;
}
验证
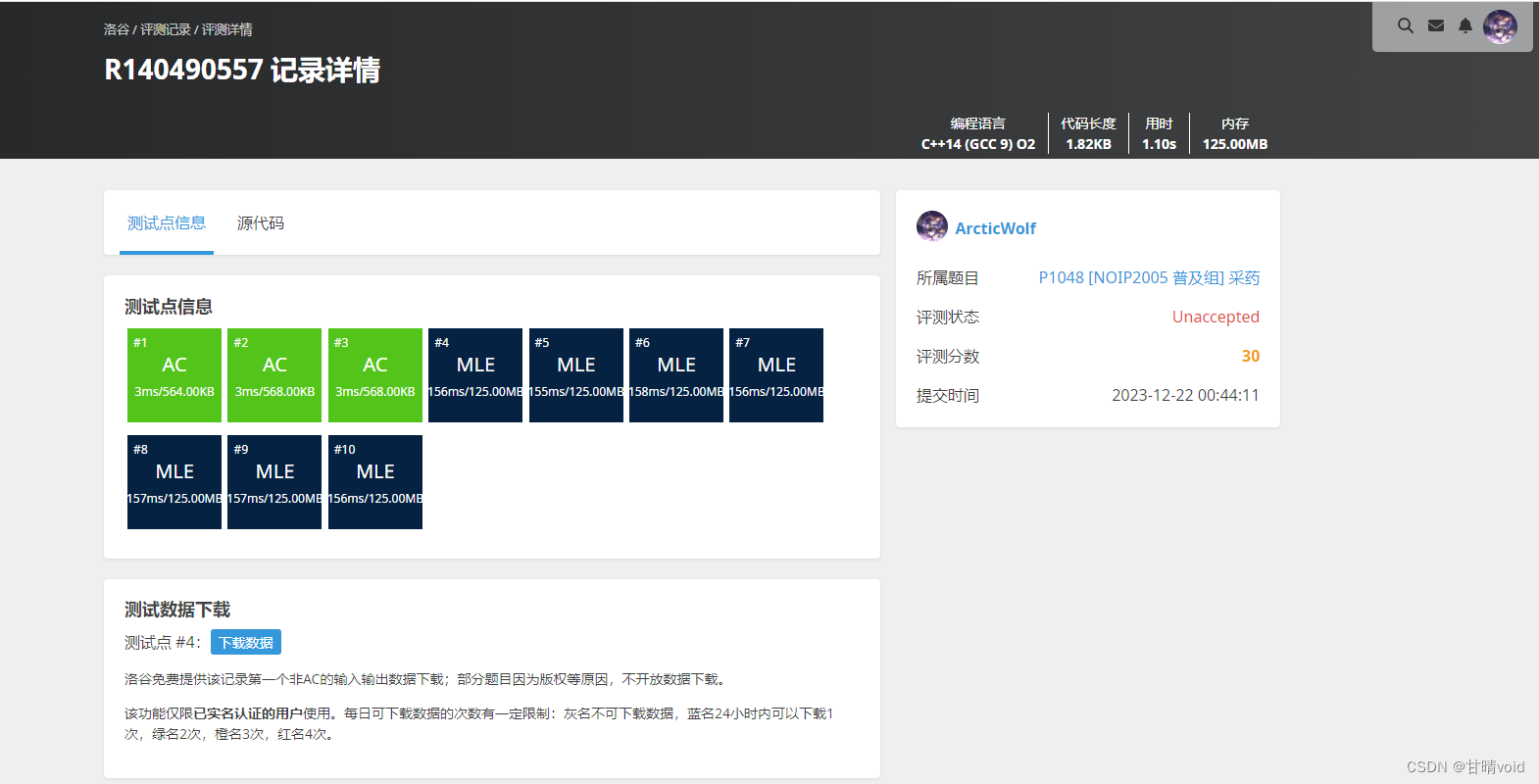
可以看到,即使优化了上界函数,使得更加精确,实际上还是没有达到更好的效果。因为队列扩展并遍历了太多的节点。这里的原因后面还会再提到,下一步将解决这个问题。
算法分析
时间复杂度:O(N*2^N),因为贪心法计算上界用了O(n)
空间复杂度:O(2^N)
【队列>优化】贪心估算bestv
想法
使用队列遍历解空间树可能超时/超空间的一个原因在于在同一层次扩展了太多的节点。这个的原因在于我们的bestv值是随着层数增长而逐渐增长的,在层数较少的时候,我们的bestv实际是很小的。这样就会导致一些右子树(“不选”的节点)的上界可能是大于我们当时的bestv,但是它实际上在我们后面更新了bestv之后发现,这个右子树的上界小于我们更新后的bestv,那么实际上这个右子树是没必要扩展的,问题就在于我们预先不知道bestv能到多大。
倘若我们能一开始确定一个正确的物品总价值bestv,那么上界达不到的右子树都会直接被除去。可以用贪心的方法计算这个bestv值,只要这个bestv值是一个正确可达的物品总价值就可以,它会在之后被更优的价值替换,并得到最终的正确结果。
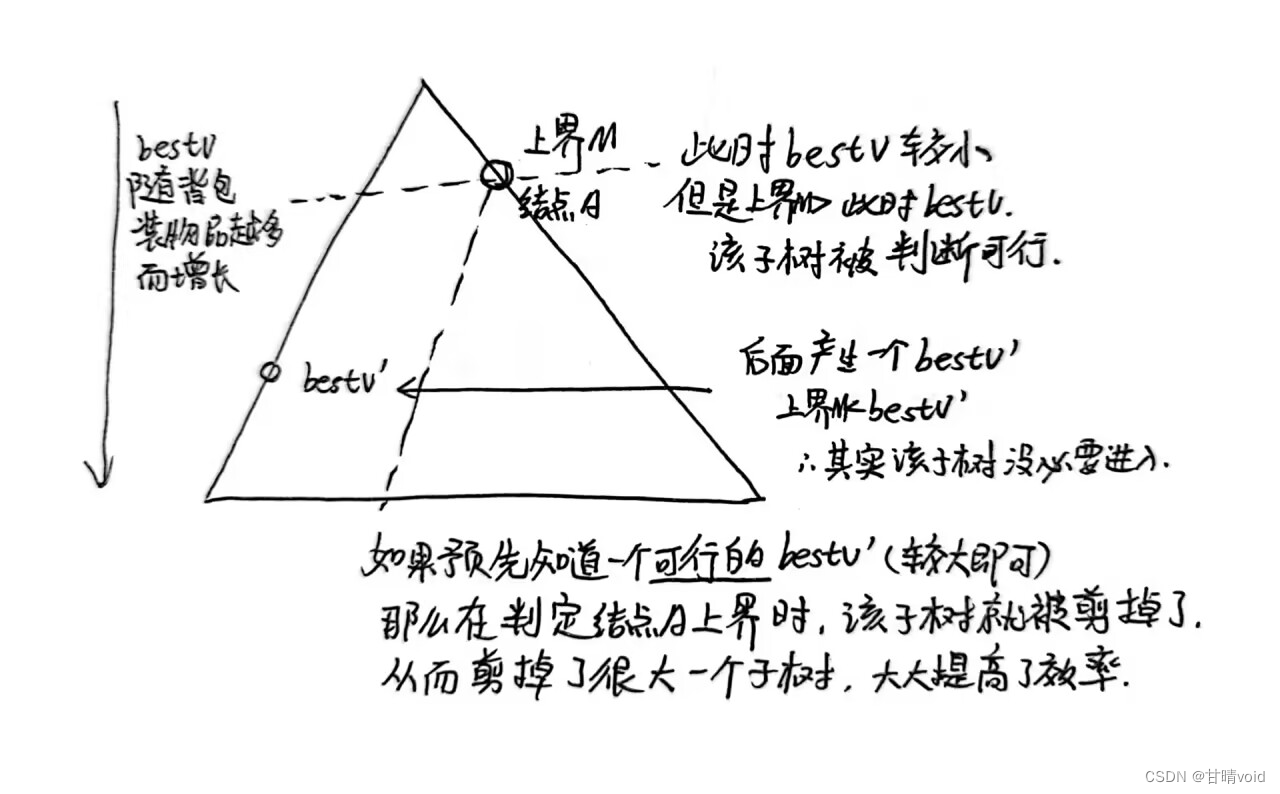
使用贪心法计算的bestv越接近最终的价值,能剪掉的枝就越多,事实上我们程序的效率就越高。
实际上,只在上一个的基础上,添加了构造可行bestv的这一段代码,就能达到AC的效果。
// 尝试预先构造出一个较大的可行bestv
int possible_bestv = 0;
int temp_weight = maxw;
int pos = 0;
while (((temp_weight - goods[pos].w) > 0) && (pos < n))
{
possible_bestv += goods[pos].v;
temp_weight -= goods[pos].w;
pos++;
}
bestv = possible_bestv;
代码3(AC)
// -*- coding:utf-8 -*-
// File : 0-1背包(分支限界法)-队列2.cpp
// Time : 2023/12/21
// Author : wolf
#include <algorithm>
#include <functional>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int rest_v[5000];
int maxw, n, bestv = 0;
// 商品:使用sort函数排序,商品价值与重量要带着走不方便,用结构体来保证
struct goods
{
int w;
int v;
double vpw;
} goods[5000];
// sort函数的排序依据:性价比较高的排在前面
bool cmp_goods(struct goods a, struct goods b)
{
return a.vpw > b.vpw;
}
// 节点:表示解空间树上的一个节点
struct Node
{
int now_w;
int now_v;
int depth;
Node(int _now_w, int _now_v, int _depth)
{
now_w = _now_w;
now_v = _now_v;
depth = _depth;
}
};
queue<Node *> q;
// 计算一个节点的总贪心价值
double get_greedy_v(int now_w, int now_v, int depth)
{
int wleft = maxw - now_w; // 剩余容量
int greedy_v = now_v; // 价值上界,函数返回值
// 以物品单位价值递减顺序排列
depth++;
while (depth < n && goods[depth].w <= wleft)
{
greedy_v += goods[depth].v;
wleft -= goods[depth].w;
depth++;
}
if (depth < n)
greedy_v += goods[depth].vpw * wleft;
return greedy_v;
}
void BFS()
{
Node *root = new Node(0, 0, -1);
q.push(root);
while (!q.empty())
{
Node *now = nullptr;
now = q.front();
q.pop();
// cout << "now:" << now->depth << endl;
if (now->depth == n) // 到达答案层
{
if (now->now_v > bestv)
bestv = now->now_v;
}
else
{
// Node(int _now_w, int _now_v, int _depth, double _rest_greedy_v)
int w = now->now_w;
int v = now->now_v;
int depth = now->depth;
// 分别计算已有的加上后面的贪心价值,这是这个节点的总贪心价值,也是优先队列的排序依据
// double fetch_greedy_v = get_greedy_v(w + goods[depth + 1].w, v + goods[depth + 1].v, depth + 1);
double drop_greedy_v = get_greedy_v(w, now->now_v, depth + 1);
if (w + goods[depth + 1].w <= maxw) // 剪枝:约束函数:排除不可行解(超重)(只需对左子树考虑)
{
if (v + goods[depth + 1].v > bestv)
{
bestv = v + goods[depth + 1].v; // 更新最优价值
}
Node *fetch = new Node(w + goods[depth + 1].w, v + goods[depth + 1].v, depth + 1);
q.push(fetch); // 取
}
if (drop_greedy_v > bestv) // 剪枝:约束函数:排除非最优解(只需对右子树考虑)
{
Node *drop = new Node(w, v, depth + 1);
q.push(drop); // 不取
}
delete (now); // 释放空间
// cout << "fetch:" << fetch_greedy_v << endl
// << "drop:" << drop_greedy_v << endl
// << endl;
}
}
}
int main()
{
cin >> maxw >> n;
for (int i = 0; i < n; i++)
{
cin >> goods[i].w >> goods[i].v;
goods[i].vpw = (double)(goods[i].v) / goods[i].w; // 计算性价比
}
sort(goods, goods + n, cmp_goods); // 预排序,使性价比较高的靠前
// 尝试预先构造出一个较大的可行bestv
int possible_bestv = 0;
int temp_weight = maxw;
int pos = 0;
while (((temp_weight - goods[pos].w) > 0) && (pos < n))
{
possible_bestv += goods[pos].v;
temp_weight -= goods[pos].w;
pos++;
// cout << "temp_weight = " << temp_weight << endl;
}
// cout << "bestv = " << possible_bestv << endl;
bestv = possible_bestv;
BFS();
cout << bestv << endl;
return 0;
}
验证
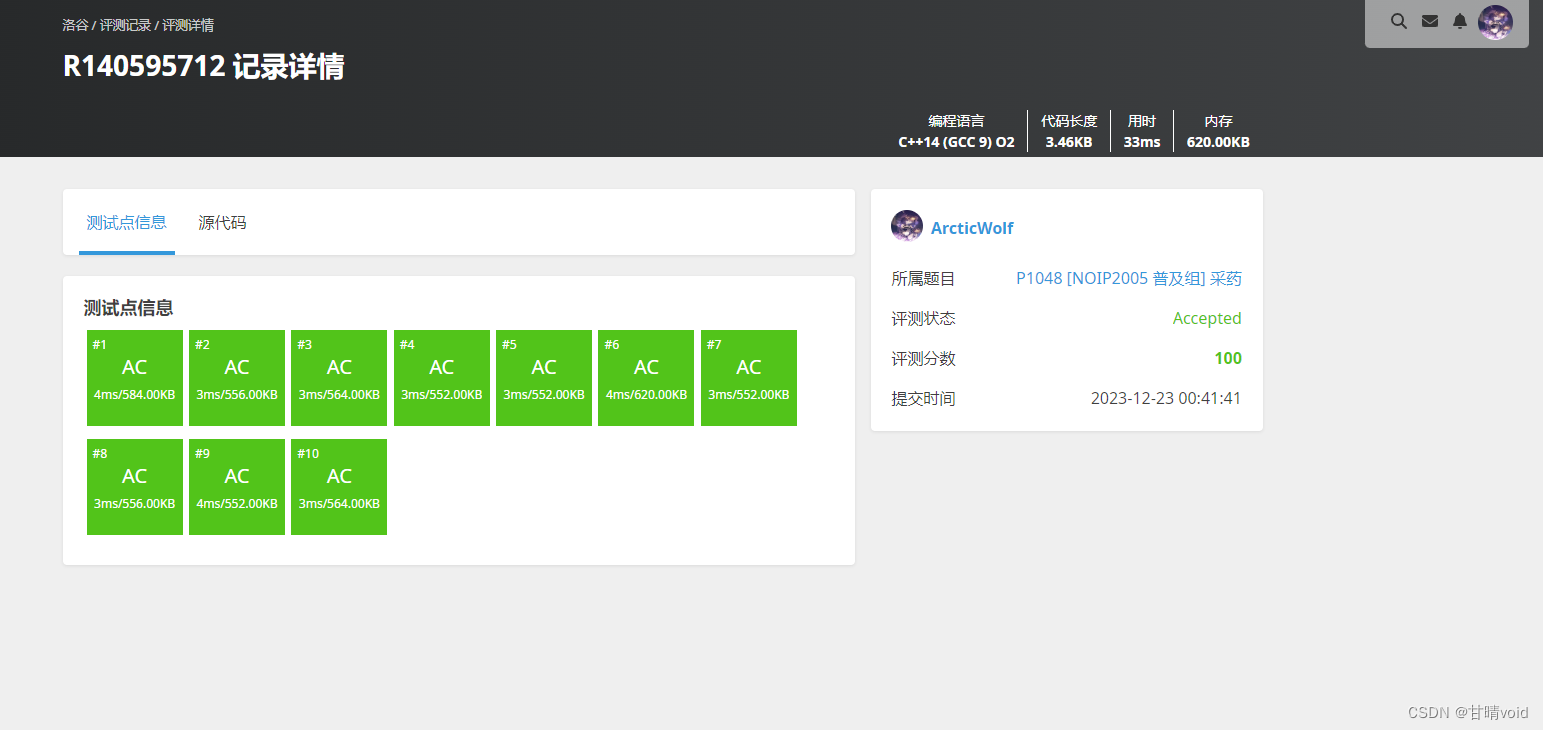
效果非常好,只是预先给定了一个bestv而已,就能AC,可见同一个算法优化一个小点,也能达到很大的进步。
算法分析
时间复杂度:O(N*2^N),因为贪心法计算上界用了O(n)
空间复杂度:O(2^N)
【优先队列实现】
想法
“优先队列”体现在“优先”。对于每个节点,计算到它已拥有的价值,与后面所有物品全部取完在完全背包下的贪心价值,按照这个来作为优先队列的排序主键。
优先队列的实现是一个二叉堆(大根堆),该堆始终保证根节点在我们想要的属性上是最大值。
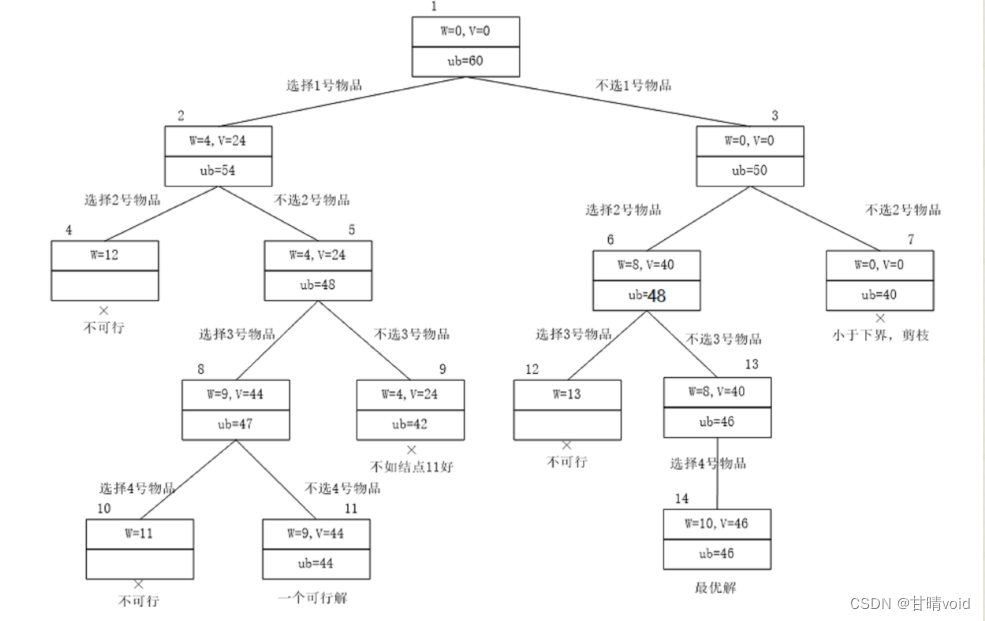
网上找到一份解决该题的“优先队列式分支限界法”流程图,大概步骤如下:
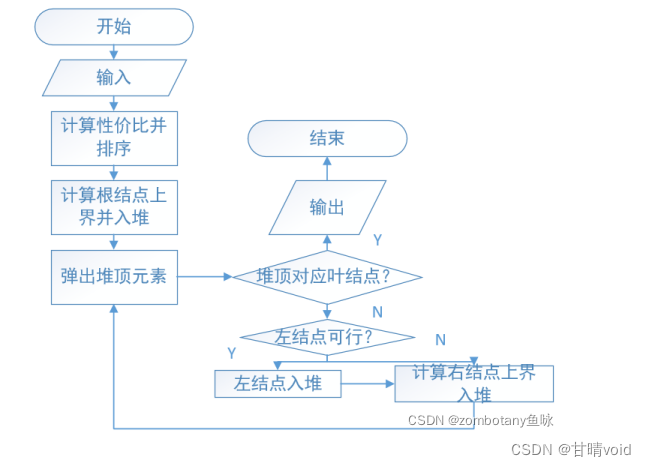
这是一个具体的例子:
(注意产生的一个可行解并没有就是最终的解,产生不等于到达,它仍然在优先队列中。此时节点13的优先级是46,而刚刚那个可行解的优先级是44,此时节点13是最先被处理的)
从这里也可以从一个侧面感知,为什么优先队列式分支限界法第一个最终到达的叶子节点就是最优解。
假设此前在队列中,该叶子节点后面还有比它更高优先级的,那么一定会先被处理。如果让一个叶子节点具有最高优先级,就表示排在它后面的节点产生的即使是贪心价值甚至都没它高,它就应该是最优解了。
这张图也可以很好地看出约束函数(因为“不可行”而被剪枝)和限界函数(因为“小于下界”而被剪枝)的作用。
以下是这个范例,ub(即upbounds)计算的是上界价值
- w[]={4,8,5,2}
- v[]={24,40,20,6}
- wmax=10
【注意这里的贪心策略使用的是用它紧邻的物品的单价填满剩余背包,跟我们上面的贪心策略不一样,但是仍然是正确的,但是在数据上会有点不一样,想法是一样的】
原连接:https://blog.csdn.net/m0_63238256/article/details/127460451(这个讲解的也很好)
有关优先队列的使用:https://blog.csdn.net/weixin_47266712/article/details/126400051
书上提供了一份代码,但是由于引入了太多类,太面向对象了,感觉晦涩难懂。我自己理解意思之后重新写了一份。
这是书本上的代码:
#include <iostream>
using namespace std;
// 背包物品类
class Object
{
friend int Knapsack(int *, int *, int, int, int *);
public:
int operator<=(Object a) const { return (d >= a.d); }
private:
int ID;
float d; // 单位重量价值
};
// 子集树中的结点类
class bbnode
{
friend Knap<int, int>;
friend int Knap(int *, int *, int, int, int *);
private:
bbnode *parent;
bool Lchild;
};
// 堆中堆结点类
class HeapNode
{
friend Knap<int, int>;
public:
operator int() const { return uprofit; }
private:
int uprofit; // 结点的价值上界
int profit; // 结点相应的价值
int weight; // 结点相应的重量
int level; // 活结点在子集树中所处的层序号
bbnode *ptr; // 指向活结点在子集树中相应结点的指针
};
// 背包类,记录当前背包的最大价值,当前价值以及容量
class Knap
{
friend int Knapsack(int *, int *, int, int, int *);
public:
int MaxKnapsack();
private:
MaxHeap<HeapNode<int, int>> *H; // 创建一个最大堆
int Bound(int i); // 计算上界函数
void AddLiveNode(int up, int cp, int cw, bool ch, int lev); // 添加活结点进入优先队列
bbnode *E; // 指向扩展结点的指针
int n; // 物品总数
int *w; // 物品重量数组
int *p; // 物品价值数组
int cw; // 当前重量
int c; // 背包容量
int cp; // 当前价值
int *bestx; // 最优解数组
};
int Knap<int, int>::Bound(int i) // 计算结点所相应的价值上界,贪心思想
{
int cleft = c - cw; // 剩余容量
int b = cp; // 价值上界,函数返回值
// 以物品单位价值递减顺序排列 补充代码
while (i <= n && w[i] <= cleft)
{
b += p[i];
cleft -= w[i];
i++
}
if (i < n)
b += p[i] / w[i] * cleft;
return b;
}
// 将活结点加入优先队列中
void Knap<int, int>::AddLiveNode(int up, int cp, int cw, bool ch, int lev)
{
bbnode *b = new bbnode;
b->parent = E; // E指向当前的扩展结点
b->Lchild = ch;
HeapNode<int, int> N;
N.ptr = b; // 指向子集树中活结点对应的结点
N.uprofit = up; // 这是优先队列的优先级,当前加入的重量+剩余可装入的最大重量(此最大重量为可加入的单位最大重量)
N.profit = cp;
N.weight = cw;
N.level = lev;
H->insert(N); // 将这个点加入到优先队列中
// 整体结构为堆的结点指向子集树的结点,然后加入堆中
}
// 按照优先级遍历子集树,将活结点加入到优先队列中
int Knap<int, int>::MaxKnapsack()
{
H = new MaxHeap<HeapNode<int, int>>(1000); // 声明一个优先队列,内部成员类型为堆结点类型
bestx = new int[n + 1]; // 记录最优解
cw = cp = 0;
int bestp = 0;
int up = Bound(1);
int i = 1;
E = 0; // 当前扩展结点为0
while (i != n + 1)
{
// 检查当前扩展结点的左儿子结点
int wt = cw + w[i];
if (wt <= c)
{
if (cp + p[i] > bestp)
{
bestp = cp + p[i];
}
AddLiveNode(up, cp + p[i], cw + w[i], true, i + 1);
}
// 这里就算的Bound只是为了给右节点一个约束,看是否有必要将右节点加入到活结点队列中
up = Bound(i + 1);
if (up >= bestp)
{
// 右节点有机会加入
AddLiveNode(up, cp, cw, false, i + 1);
}
// 取下一扩展结点
HeapNode<int, int> N;
H->DelMax(N);
up = N.uprofit; // 更新最大价值
cp = N.profit; // 更新当前价值,为新的扩展结点的价值
cw = N.weight; // 更新当前重量,为新的扩展结点的重量
E = N.ptr; // 下一扩展点,子集树中的点
i = N.lev;
}
for (int j = n; j > 0; j--)
{
bestx[j] = E->Lchild; // 将路径解记录下来
E = E->parent; // 逐渐向上遍历找出路径上的具体添加方案
}
}
// Knapsack函数完成对输入数据的预处理,我们输入的object类的物品,根据我们的最大上界函数即Bound函数可知
// 我们需要将单位重量的价格从大到小排序,从而计算Bound,将其作为优先级
// 所以这个函数的作用是将输入的Object类对象排序传递给Knap类对象,返回最大价值
int Knapsack(int p[], int w[], int c, int n, int bestx[])
{
// 初始化
int W = 0; // 装包物品重量
int P = 0; // 装包物品价值
Object *Q = new Object[n]; // 依单位重量价值排序的物品数组
for (int i = 1; i <= n; i++)
{
// 单位重量价值数组
Q[i - 1].ID = i;
Q[i - 1].d = 1.0 * p[i] / w[i];
P += p[i];
W += w[i];
}
if (W <= c)
{
return P;
}
Sort(Q, n); // 这里自定义一个函数依单位重量价值排序
// 先将代表序号的数组按照性价比排序,再对照着这个数组把物品构建好
// 创建类Knap的数据成员
Knap<int, int> K;
K.p = new int[n + 1];
K.w = new int[n + 1];
for (int i = 1; i <= n; i++)
{
K.p[i] = p[Q[i - 1].ID];
K.w[i] = w[Q[i - 1].ID]; // 按照单位重量价值排好序的价值和重量数组
}
K.cp = 0;
K.cw = 0;
K.c = c;
K.n = n;
int bestp = K.MaxKnapsack(); // 调用函数求问题的最优解
for (int j = 1; j <= n; j++)
{
bestx[Q[j - 1].ID] = K.bestx[j];
}
delete[] Q;
delete[] K.w;
delete[] K.p;
delete[] K.bestx;
return bestp;
}
这是书上的代码,之后会有我自己的实现。
代码4(AC)
// -*- coding:utf-8 -*-
// File : 0-1背包(分支限界法)-优先队列.cpp
// Time : 2023/12/21
// Author : wolf
#include <algorithm>
#include <functional>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int rest_v[5000];
int maxw, n, bestv = 0;
// 商品:使用sort函数排序,商品价值与重量要带着走不方便,用结构体来保证
struct goods
{
int w;
int v;
double vpw;
} goods[5000];
// sort函数的排序依据:性价比较高的排在前面
bool cmp_goods(struct goods a, struct goods b)
{
return a.vpw > b.vpw;
}
// 节点:表示解空间树上的一个节点
struct Node
{
int now_w;
int now_v;
int depth;
double greedy_v; // 总贪心价值
Node(int _now_w, int _now_v, int _depth, double _greedy_v)
{
now_w = _now_w;
now_v = _now_v;
depth = _depth;
greedy_v = _greedy_v;
}
};
// 优先队列的构造依据:总贪心价值高的排在队列开始
struct cmp_node
{
bool operator()(Node *a, Node *b)
{
return a->greedy_v < b->greedy_v;
}
// 这里的大小方向似乎与正常的要反一下
};
// 建立优先队列
// priority_queue<Type, Container, Functional>
// 其中Type代表数据类型,Container代表容器类型,缺省状态为vector; Functional是比较方式,默认采用的是大顶堆(less<>)
priority_queue<Node *, vector<Node *>, cmp_node> q;
// 计算一个节点的总贪心价值
double get_greedy_v(int now_w, int now_v, int depth)
{
int wleft = maxw - now_w; // 剩余容量
int greedy_v = now_v; // 价值上界,函数返回值
// 以物品单位价值递减顺序排列
depth++;
while (depth < n && goods[depth].w <= wleft)
{
greedy_v += goods[depth].v;
wleft -= goods[depth].w;
depth++;
}
if (depth < n)
greedy_v += goods[depth].vpw * wleft;
return greedy_v;
}
void BFS()
{
Node *root = new Node(0, 0, -1, get_greedy_v(0, 0, -1));
q.push(root);
while (!q.empty())
{
Node *now = nullptr;
now = q.top();
q.pop();
// cout << "now:" << now->depth << endl;
if (now->depth == n) // 到达答案层
{
bestv = now->now_v;
break;
}
else
{
// Node(int _now_w, int _now_v, int _depth, double _rest_greedy_v)
int w = now->now_w;
int v = now->now_v;
int depth = now->depth;
// 分别计算已有的加上后面的贪心价值,这是这个节点的总贪心价值,也是优先队列的排序依据
double fetch_greedy_v = get_greedy_v(w + goods[depth + 1].w, v + goods[depth + 1].v, depth + 1);
double drop_greedy_v = get_greedy_v(w, now->now_v, depth + 1);
if (w + goods[depth + 1].w <= maxw) // 剪枝:约束函数:排除不可行解(超重)(只需对左子树考虑)
{
if (v + goods[depth + 1].v > bestv)
{
bestv = v + goods[depth + 1].v; // 更新最优价值
}
Node *fetch = new Node(w + goods[depth + 1].w, v + goods[depth + 1].v, depth + 1, fetch_greedy_v);
q.push(fetch); // 取
}
if (drop_greedy_v > bestv) // 剪枝:约束函数:排除非最优解(只需对右子树考虑)
{
Node *drop = new Node(w, v, depth + 1, drop_greedy_v);
q.push(drop); // 不取
}
delete (now); // 释放空间
// cout << "fetch:" << fetch_greedy_v << endl
// << "drop:" << drop_greedy_v << endl
// << endl;
}
}
}
int main()
{
cin >> maxw >> n;
for (int i = 0; i < n; i++)
{
cin >> goods[i].w >> goods[i].v;
goods[i].vpw = (double)(goods[i].v) / goods[i].w; // 计算性价比
}
sort(goods, goods + n, cmp_goods); // 预排序,使性价比较高的靠前
BFS();
cout << bestv << endl;
return 0;
}
验证
洛谷P1048(https://www.luogu.com.cn/problem/P1048)
使用优先队列但不使用约束函数和上界函数进行剪枝:
使用约束函数和上界函数进行剪枝:
这比回溯法效果好太多了。
算法分析
时间复杂度:O(N*2N),与回溯法相同。当然事实上不可能这么高,这是一个非常松的上界。实际上,回溯法和分支限界法都比号称O(N2)时间复杂度的动态规划快,这证明剪枝剪去了非常多的枝条。
空间复杂度:O(2^N)。这是个非常松的上界,因为我们剪去了很多树枝,事实上从运行空间大小来看,与回溯法差不多,我们有理由相信经过剪枝后的分支限界法的运行空间在大多数情况下是接近O(N)的。
4 分支限界法求解实现题6-3无向图的最大割问题
问题重述
给定一个无向图G=(V, E),设U?V是G的顶点集。对任意(u, v)∈E,若u∈U,且v∈V-U,就称(u, 1)为关于顶点集U的一条割边。顶点集U的所有割边构成图G的一个割。G的最大割是指G中所含边数最多的割。
对于给定的无向图G,设计一个优先队列式分支限界法,计算G的最大割。
测试样例:
输入:
7 18
1 4
1 5
1 6
1 7
2 3
2 4
2 5
2 6
2 7
3 4
3 5
3 6
3 7
4 5
4 6
5 6
5 7
6 7
输出
12
1 1 1 0 1 0 0
为方便理解,我画了一张图
这是原图
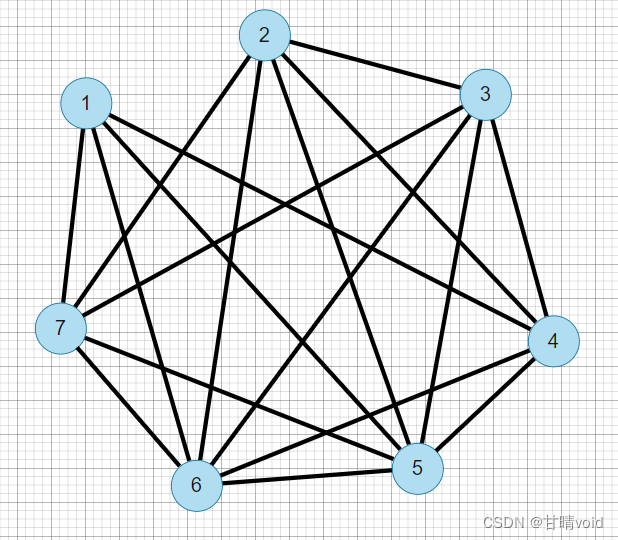
这是(其中一个)答案
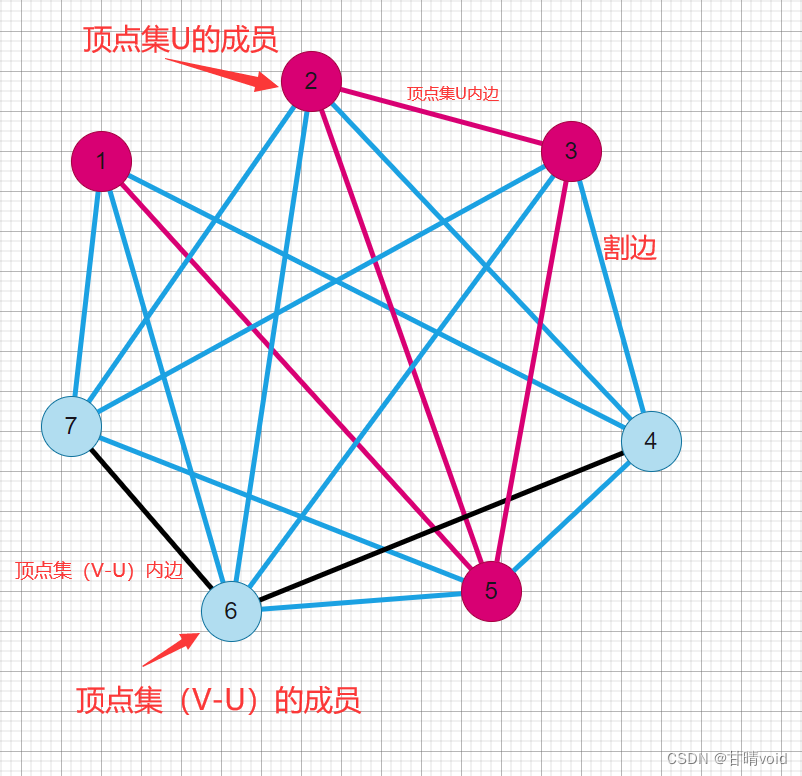
事实上。所有的点被划分为两部分,所有的边因此别划分为三部分:某个点集内部的边,或者联通两个点集的边(这个就是割边),我们要求的是割边数量的最大值和割边数量最大时,点集的划分方式(可能不唯一)。
想法
分支限界法的几个关键点
-
解向量:(x1,x2,……xn)是一个01序列,其中xi=1表示点xi在割集,0表示不在割集
-
解空间:完全二叉树,子集树
-
-
约束函数:无
-
上界函数:只有考察右子结点的时候,需要判断是否剪枝:假设当前的割边数加上剩余的边数都没有最优解大,那么就剪去。
-
优先队列优先级依据:每个结点的当前割边数
★本题需要注意的:如何更新一个状态的割边数?
对于新扩展出的子节点状态M:
如果这个节点M是“不取”,那么显然割边数和剩余边数没有发生变化,不用改动;
如果这个节点M是“取”,那么遍历所有节点K,并处理与这个节点M存在边的节点K。如果节点K不在我划分的点集内,那么M与K是会新产生一条割边,割边数需要增加,剩余边数需要减少。如果节点K已经在我划分的点集内,那么;对于刚刚不在点集内的M的加入,实际上会减少一条割边,但剩余边数并没有减少。这一段逻辑的实现代码如下:
(这一段逻辑也可以暴力遍历所有边,然后看两边的点是否在同一个集合内这样计算割边数目,这样的时间复杂度代价是边数E)
for (int i = 0; i < n; i++)
{
if (Graph[depth + 1][i])
{
if (!status[i])
{
now_cut++;
left_edge--;
}
else
{
now_cut--;
}
}
}
此外由于最终需要输出划分方式,以及判断某个点是否已经在点集内,我维持了一个数组status[i],表示点i在该状态下是否属于这个点集合。
参考文献
https://blog.csdn.net/qq_43496675/article/details/106540412
https://codeleading.com/article/78203823112/
代码
// -*- coding:utf-8 -*-
// File : 实现题6-3.cpp
// Time : 2023/12/22
// Author : wolf
#include <iostream>
#include <queue>
using namespace std;
int n, e; // 顶点数和边数
int Graph[200][200]; // 存储图的邻接矩阵
int bestcut = 0; // 存储最优解:最大割
int bestx[200], status[200]; // 存储最优解:解向量
using namespace std;
struct Node
{
int depth;
int now_cut;
int left_edge;
int status[200];
Node(int _depth, int _now_cut, int _left_edge)
{
depth = _depth;
now_cut = _now_cut;
left_edge = _left_edge;
}
// 确定优先队列优先级
// bool operator<(const Node &node) const
//{
// return now_cut < node.now_cut;
//}
};
// 优先队列的构造依据
struct cmp_node
{
bool operator()(Node *a, Node *b)
{
return a->now_cut < b->now_cut;
}
// 这里的大小方向似乎与正常的要反一下
};
priority_queue<Node *, vector<Node *>, cmp_node> q;
void solve_maxcut()
{
Node *root = new Node(-1, 0, e);
for (int i = 0; i < n; i++)
status[i] = 0;
for (int i = 0; i < n; i++)
root->status[i] = status[i];
q.push(root);
while (!q.empty())
{
Node *now = nullptr;
now = q.top();
q.pop();
int depth = now->depth;
// cout << depth << endl;
int now_cut = now->now_cut;
int left_edge = now->left_edge;
for (int i = 0; i < n; i++)
status[i] = now->status[i];
// 到达答案层
if (depth == n - 1)
{
if (now_cut >= bestcut)
{
bestcut = now_cut;
for (int i = 0; i < n; i++)
bestx[i] = status[i];
// for (int i = 0; i < n; i++)
// cout << status[i] << " ";
// cout << endl;
}
// break;
}
else
{
// 不取
if (now_cut + left_edge > bestcut) // 剪枝
{
Node *drop = new Node(depth + 1, now_cut, left_edge);
for (int i = 0; i < n; i++)
drop->status[i] = status[i];
q.push(drop);
}
// 取
for (int i = 0; i < n; i++)
{
if (Graph[depth + 1][i])
{
if (!status[i])
{
now_cut++;
left_edge--;
}
else
{
now_cut--;
}
}
}
status[depth + 1] = 1;
Node *fetch = new Node(depth + 1, now_cut, left_edge);
for (int i = 0; i < n; i++)
fetch->status[i] = status[i];
q.push(fetch);
}
}
}
int main()
{
int u, v;
cin >> n >> e;
for (int i = 0; i < e; i++)
{
cin >> u >> v;
Graph[u - 1][v - 1] = 1;
Graph[v - 1][u - 1] = 1;
}
solve_maxcut();
cout << bestcut << endl;
for (int i = 0; i < n; i++)
{
cout << bestx[i] << " ";
}
cout << endl;
return 0;
}
验证
本题没有找到在线评测,所以自己尝试数据进行验证。
案例测试数据
使用题目给定的数据进行验证。
验证截图如下:
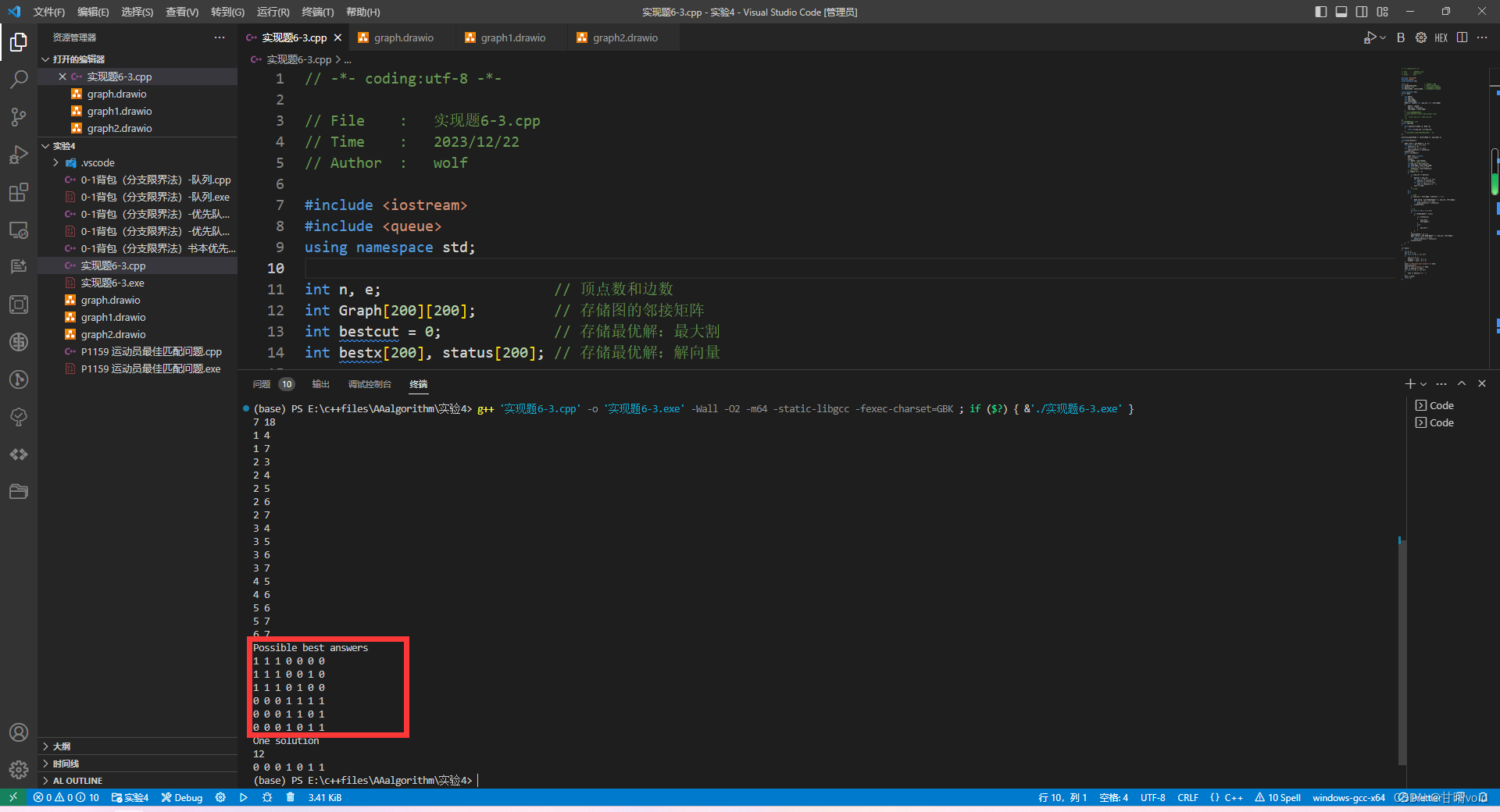
结果如下:
Possible best answers
1 1 1 0 0 0 0
1 1 1 0 0 1 0
1 1 1 0 1 0 0
0 0 0 1 1 1 1
0 0 0 1 1 0 1
0 0 0 1 0 1 1
One solution
12
0 0 0 1 0 1 1
我先输出了所有可能的最优结果,然后输出了其中一个最优结果。
可能有点好奇,明明题目只提供了一种最优解啊,前面说过,这个划分实际上可能是不唯一的。以1 1 1 0 0 0 0为例,其最大割也是12。
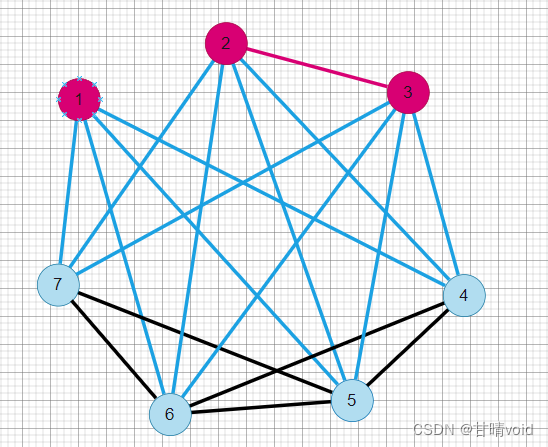
事实上,这里看似有6个结果,实际上只有3种划分方法,因为0和1只起到划分开两个点集的作用,一边是0另一边是1和反过来其实是对称的,是一种划分方法,只不过谁是U和谁是(V-U)的区别。
自定义测试数据
再来测试一个大一点的数据
11 37
1 2
1 3
1 4
1 6
1 8
1 9
1 11
2 4
2 5
2 6
2 8
2 10
3 4
3 5
3 7
3 9
3 10
3 11
4 5
4 6
4 7
4 8
4 11
5 6
5 7
5 9
5 10
6 7
6 8
6 9
7 9
7 10
8 9
8 11
9 10
9 11
10 11
这个案例的示意图
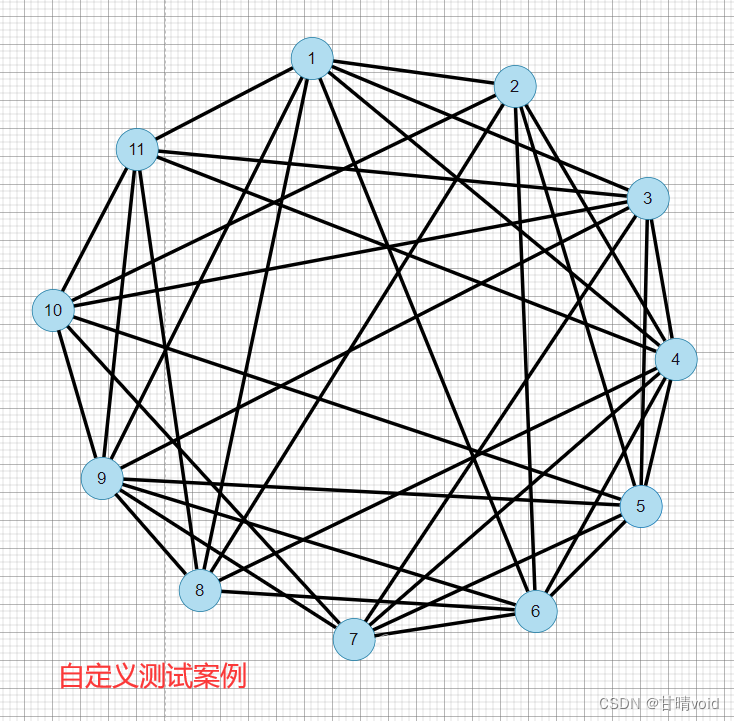
测试结果(只看一个)
One solution
24
1 1 0 0 1 0 1 1 0 0 1
测试结果可视化图:
(红色点集内边7个,蓝色点集内边6个,黑色边【也就是割边】24个,总边37个)
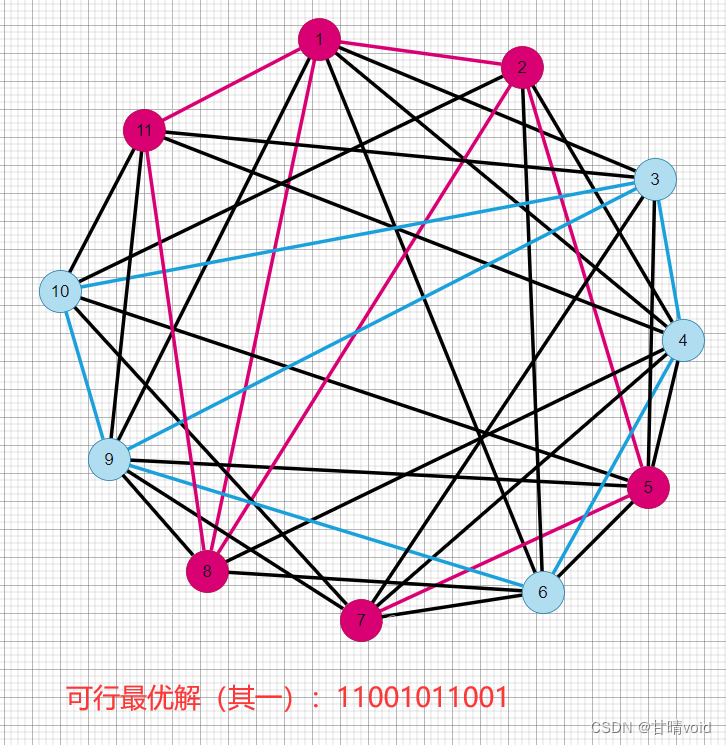
算法分析
时间复杂度:O(N*2N),与回溯法相同,当然了,事实上不可能这么高,这是一个非常松的上界,相信不难发现回溯法和分支限界法都比号称O(N2)时间复杂度的动态规划快,这证明剪枝剪去了非常多的枝条。
空间复杂度:O(2^N),这是个非常松的上界,因为我们剪去了很多树枝,事实上从运行空间大小来看,与回溯法相差无几,我们有理由相信经过剪枝后的分支限界法的运行空间在大多数情况下是接近O(N)的。
实验感悟
主要是完成了2道回溯题,2道分支限界题,题目限定了解题方法,主要对回溯法与分支限界法的区分做了更进一步的理解,完成之后感觉还是有收获的。
特别是分支限界法,感觉还是没那么简单的。
特别是分支限界法的优先队列实现,感觉还是有些难理解的。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Redis主从复制、哨兵模式、群集模式
- C# LINQ
- python之画动态图 gif效果图
- 算法通关村第十九关-白银挑战动态规划高频问题
- 【软件安装】史上最好玩的游戏——3D Mark的安装
- 中国存储器行业概述
- 中小企业如何做好信息化规划?
- 无代码DIY图像检索
- 标签正则化和硬标签、软标签、单标签、多标签
- 【Arduino】基于 I2C 模块通过 I2C 接口驱动 LCD1602 字符液晶显示模块显示文本:只需两个引脚即可控制 LCD1602 液晶屏