【LeetCode刷题笔记（10-1）】【Python】【找到字符串中所有字母异位词】【滑动窗口】【中等】

找到字符串中所有字母异位词

---

引言

编写通过所有测试案例的代码并不简单，通常需要深思熟虑和理性分析。虽然这些代码能够通过所有的测试案例，但如果不了解代码背后的思考过程，那么这些代码可能并不容易被理解和接受。我编写刷题笔记的初衷，是希望能够与读者们分享一个完整的代码是如何在逐步的理性思考下形成的。我非常欢迎读者的批评和指正，因为我知道我的观点可能并不完全正确，您的反馈将帮助我不断进步。如果我的笔记能给您带来哪怕是一点点的启示，我也会感到非常荣幸。同时，我也希望我的分享能够激发您的灵感和思考，让我们一起在编程的道路上不断前行~

找到字符串中所有字母异位词

题目描述

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

• 异位词：指由相同字母重排列形成的字符串（包括相同的字符串）。

---

示例 1:

• 输入: s = “cbaebabacd”, p = “abc”
• 输出: [0,6]
• 解释:
  • 起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
  • 起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。

示例 2:

• 输入: s = “abab”, p = “ab”
• 输出: [0,1,2]
• 解释:
  • 起始索引等于 0 的子串是 “ab”, 它是 “ab” 的异位词。
  • 起始索引等于 1 的子串是 “ba”, 它是 “ab” 的异位词。
  • 起始索引等于 2 的子串是 “ab”, 它是 “ab” 的异位词。

---

提示

• 1 <= s.length, p.length <= 3 * 10⁴
• s 和 p 仅包含小写字母

---

解决方案1：【滑动窗口】

根据题意，我们需要关注如何在字符串 s 中准确找到所有 p 的异位词的子串。为了深入理解这个问题，我们可以参考博客【LeetCode刷题笔记（9-1）】【Python】【无重复字符的最长子串】【滑动窗口】【中等】中的对【无重复字符的最长子串】问题的解析。在博客中，我们逐步理性地分析了题意和示例，从中挖掘出一些重要的规律。正是基于这些规律，我们自然而然地引入了【滑动窗口】这个解决方案。

与【无重复字符的最长子串】相比，【找到字符串中所有字母异位词】有其相似之处，但也存在一些不同。如下表所示：

	无重复字符的最长子串	找到字符串中所有字母异位词
是否需要维护窗口	需要在遍历中保持窗口内不存在无重复字符	需要使用窗口对字符串s进行截断，获取子串和字符串p进行比较
窗口长度是否定长	窗口截断字符串s生成子串 —> 找到无重复字符的最长子串 —> 窗口不定长	窗口截断字符串s生成子串 —> 检查子串是否和字符串p互为字母异位词 —> 字符串p的长度是固定的，和p的长度一致的子串对比才有意义 —> 窗口定长，且长度一定是字符串p的长度
存储窗口元素的数据结构是否需要方便获取窗口长度？	目标是找到无重复字符的最长子串 —> 需要	窗口定长 —> 不需要
是否能确定窗口的起始位置/终止位置	当遍历s第i个字符时，窗口的终止位置是i，由于窗口不定长，无法提前确定窗口的起始位置	当遍历s第i个字符时， 若窗口的起始位置是i，终止位置是i+len(p)-1 ； 若窗口的终止位置是i，终止位置是i-len(p)+1—> 循环时注意索引不要越界
是否可以用集合set()存储窗口元素，模拟队列数据结构	可以，该问题关键在于查找指定字符是否存在于窗口中 ? 关键在于查找 ，不要求窗口元素有序 ? 集合set()可以进一步优化查找速度	不可以，因为需要对比子串和p是否互为字母异位词 ? 关键在于对比 ，互为字母异位词的排序结果相同，有利于对比 ? 不能用集合set()，因为集合无法排序，不利于对比
未完待续…

完整代码如下：

class Solution:  
    def findAnagrams(self, s: str, p: str) -> List[int]:  
        # 获取字符串s和p的长度  
        s_len = len(s)  
        p_len = len(p)  
          
        # 对字符串p进行排序  
        # sorted(p)会把排序好的字符串以列表形式返回，通过字符串的join方法重新转换为字符串
        sorted_p = "".join(sorted(p))  
          
        # 初始化结果列表  
        result_list = []  
  
        # 遍历字符串s
        for i in range(s_len):
            # 如果窗口的终止索引超过字符串的索引范围
            if i + len(p) - 1 > s_len - 1:
                break # 退出循环，返回结果列表
            # 对从i开始的p_len个字符进行排序 --> s[i:i+p_len]就是窗口  
            cur_sorted_strs = "".join(sorted(s[i:i+p_len]))  
              
            # 如果排序后的字符串与sorted_p相等，则说明找到了一个匹配的子字符串，将起始索引i添加到结果列表中  
            if cur_sorted_strs == sorted_p:  
                result_list.append(i)  
          
        # 返回结果列表  
        return result_list

运行结果：

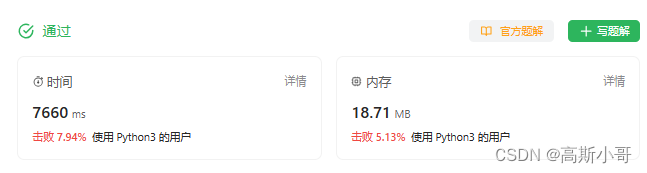
问题1：从运行结果来看，存在巨大的优化空间，代码哪些部分占用了大部分时间呢？

从时间复杂度上看，在每个循环逻辑下，耗时最长的应当是对子串进行排序。假设字符串s的长度为N，字符串p的长度为M，那么每个子串的长度也为M ? 每个循环下的时间复杂度为O(MlogM) ? 总时间复杂度O(N * MlogM)。

问题2：for循环遍历字符串s肯定是必要的，那么能不能在【不需要排序】的情况下，实现字母异位词的对比？

可以！突破局限，转换思路。

在上面的理性分析中，我们提出同时对子串和字符串p进行先排序后比较的策略，以验证给定窗口的子串是否与字符串p互为字母异位词。当字符串p的长度较小时，这么做无可厚非，但当字符串p的长度很大时，排序算法复杂度O(MlogM)的局限性就出现了。且题意告诉我们，1 <= s.length, p.length <= 3 * 10^4 ==> 字符串p的长度上限已经很大，排序算法顶不住了！

问题3：还有哪些策略可以实现字母异位词的对比呢？

如果两个字符串互为字母异位词，既然它们的排序结果相同，那么每个字符的出现次数也必然相同。更重要的是，字母的个数是有限的(上限26个) ? 我们可以使用两个长度为26的列表p_count和s_count，分别记录字符串p和子串各个字母出现的次数。其中，p_count是固定的，不会变化。而s_count中的元素会随着对字符串s的遍历动态变化(子串一直在变)。

完整代码如下：

class Solution:  
    def findAnagrams(self, s: str, p: str) -> List[int]:  
        """  
        查找字符串s中与p长度相同的所有异位词子串  
  
        参数:  
            s (str): 源字符串  
            p (str): 目标字符串  
  
        返回:  
            List[int]: 异位词子串的起始索引列表  
        """  
        s_len, p_len = len(s), len(p)  
  
        # 如果源字符串长度小于目标字符串长度，直接返回空列表  
        if s_len < p_len:  
            return []  
  
        # 初始化结果列表  
        result_list = []  
  
        # 初始化计数数组，用于记录p和给定子串中每个字符出现的次数  
        p_count = [0] * 26  
        s_count = [0] * 26  
  
        # 遍历目标字符串p，统计每个字符出现的次数  
        for i in range(p_len):  
            p_count[ord(p[i]) - ord("a")] += 1  
            # 同时更新窗口内子串的字符计数
            s_count[ord(s[i]) - ord("a")] += 1  
  
        # 如果目标字符串p的字符计数与窗口内子串的字符计数相等，则说明p和子串互为异位词，起始索引为0，将0添加到结果列表中  
        if p_count == s_count:  
            result_list.append(0)  
  
        # 从目标字符串长度开始，每次移动窗口，统计窗口内子串每个字符出现的次数，并与目标字符串p的字符计数进行比较  
        for i in range(p_len, s_len):  
            # 移动窗口，更新窗口内子串字符的计数 
            s_count[ord(s[i-p_len]) - ord("a")] -= 1  
            s_count[ord(s[i]) - ord("a")] += 1  
            # 如果目标字符串p的字符计数与子串的字符计数相等，则说明p和当前子串互为异位词，起始索引为i-p_len+1（窗口的起始索引），将起始索引添加到结果列表中  
            if p_count == s_count:  
                result_list.append(i-p_len+1)  
                  
        # 返回结果列表  
        return result_list

运行结果：

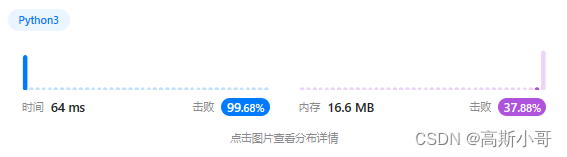
复杂度分析

• 时间复杂度：参考官方题解
• 空间复杂度：参考官方题解

结束语

• 亲爱的读者，感谢您花时间阅读我们的博客。我们非常重视您的反馈和意见，因此在这里鼓励您对我们的博客进行评论。
• 您的建议和看法对我们来说非常重要，这有助于我们更好地了解您的需求，并提供更高质量的内容和服务。
• 无论您是喜欢我们的博客还是对其有任何疑问或建议，我们都非常期待您的留言。让我们一起互动，共同进步！谢谢您的支持和参与！
• 我会坚持不懈地创作，并持续优化博文质量，为您提供更好的阅读体验。
• 谢谢您的阅读！