leetcode:2132. 用邮票贴满网格图【二维前缀和 + 二维差分模版题】
发布时间:2023年12月17日
题目截图
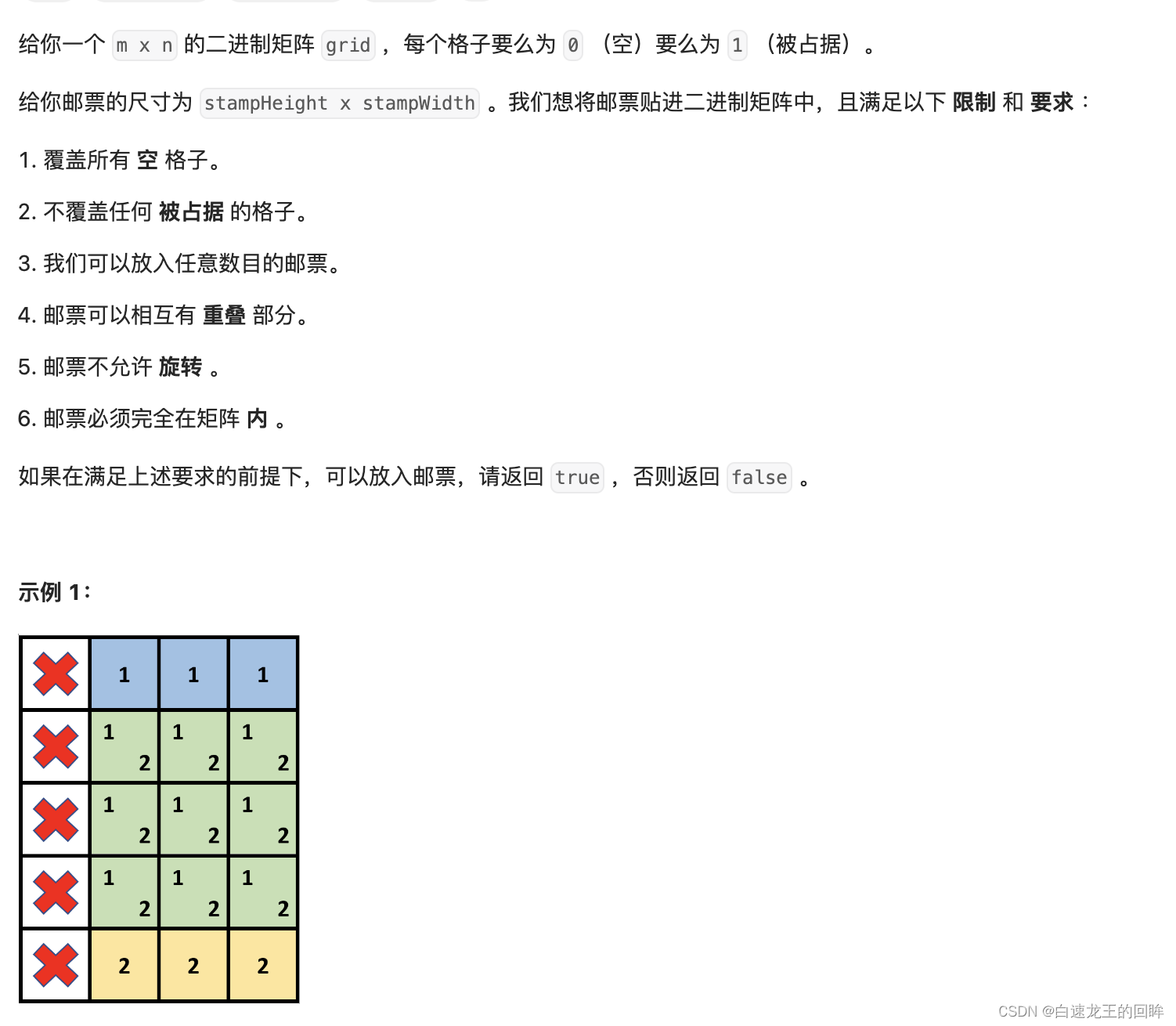
题目分析
遍历每个空白的位置,能贴就贴
能贴 = 用二维前缀和为0判断
贴上去 = 二维差分贴上去
判断 = 二维差分还原
ac code
class Solution:
def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
m, n = len(grid), len(grid[0])
# 1. 计算 grid 的二维前缀和
s = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(grid):
for j, v in enumerate(row):
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + v
# 2. 计算二维差分
# 为方便第 3 步的计算,在 d 数组的最上面和最左边各加了一行(列),所以下标要 +1
d = [[0] * (n + 2) for _ in range(m + 2)]
for i2 in range(stampHeight, m + 1):
for j2 in range(stampWidth, n + 1):
i1 = i2 - stampHeight + 1
j1 = j2 - stampWidth + 1
if s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0:
d[i1][j1] += 1
d[i1][j2 + 1] -= 1
d[i2 + 1][j1] -= 1
d[i2 + 1][j2 + 1] += 1
# 3. 还原二维差分矩阵对应的计数矩阵(原地计算)
for i, row in enumerate(grid):
for j, v in enumerate(row):
d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j]
if v == 0 and d[i + 1][j + 1] == 0:
return False
return True
文章来源:https://blog.csdn.net/weixin_40986490/article/details/134990839
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章