深度强化学习Task1：马尔可夫过程、DQN算法回顾

本篇博客是本人参加Datawhale组队学习第一次任务的笔记
【教程地址】https://github.com/datawhalechina/joyrl-book
【强化学习库JoyRL】https://github.com/datawhalechina/joyrl/tree/main
【JoyRL开发周报】 https://datawhale.feishu.cn/docx/OM8fdsNl0o5omoxB5nXcyzsInGe?from=from_copylink
【教程参考地址】https://github.com/datawhalechina/easy-rl

绪论

1. 为什么学习强化学习？
   对于任意问题，只要能够建模成序列决策问题或者带有鲜明的试错学习特征，就可以使用强化学习来解决，并且这是截至目前最为高效的方法之一。

2. 强化学习的应用有哪些？

   • 游戏领域，例如ALphaGo
   • 机器人领域，例如机器人学习抓取任务的过程
     
   • 金融领域，例如股票交易、期货交易、外汇交易等
   • 自动驾驶、推荐系统、交通派单、广告投放以及GhatGPT等

3. 强化学习的方向有哪些？

   • 多智能体强化学习：在多个智能体的环境下进行强化学习。与单智能体环境不同，在多智能体环境中通常存在非静态问题，即环境的状态不仅由智能体的动作决定，还受到其他智能体的动作的影响。
   • 从数据中学习
     • 模仿学习为代表的从专家数据中学习策略 ：指在奖励函数难以明确定义或者策略本身就很难学出来的情况下，我们可以通过模仿人类的行为来学习到一个较好的策略。最典型的模仿策略之一就是行为克隆，即将每一个状态-动作对视为一个训练样本，并使用监督学习的方法（如神经网络）来学习一个策略。但这种方法容易受到分布漂移的影响。智能体可能会遇到从未见过的状态，导致策略出错。
     • 逆强化学习(IRL)为代表的从人类数据中学习奖励函数：通过观察人类的行为来学习到一个奖励函数，然后通过强化学习来学习一个策略
     • 人类反馈中学习(RLHF)为代表的从人类标注的数据中学习奖励模型来进行微调
     • 离线强化学习
     • 世界模型
   • 探索策略：即如何在探索和利用之间做出权衡。在探索的过程中，智能体会尝试一些未知的动作，从而可能会获得更多的奖励，但同时也可能会遭受到惩罚。而在利用的过程中，智能体会选择已知的动作，从而可能会获得较少的奖励，但同时也可能会遭受较少的惩罚。
   • 实时环境
     • 离线强化学习
     • 世界模型
   • 多任务强化学习
     • 联合训练：将多个任务的奖励进行加权求和，然后通过强化学习来学习一个策略
     • 分层强化学习 ：将多个任务分为两个层次，一个是高层策略，另一个是低层策略。高层策略的作用是决策当前的任务，而低层策略的作用是决策当前任务的动作。这样就可以通过强化学习来学习高层策略和低层策略，从而解决多任务强化学习的问题。

4. 强化学习与深度学习的联系？
   深度学习在强化学习中扮演的角色主要是提供了一个强大的函数拟合能力，使得智能体能够处理复杂、高维度和非线性的环境。深度学习与强化学习之间的关系相当于眼睛和大脑的关键，眼睛是帮助大脑决策更好地观测世界的工具，对于一些没有眼睛的动物例如蚯蚓也可以通过其他的感官来观测并解析状态。

5. 强化学习的算法大致可以分为哪几类？
   强化学习算法基本上就分为两类，即基于价值的和基于策略梯度的算法

马尔可夫决策过程

马尔可夫决策过程的描述

马尔可夫决策过程是强化学习的基本问题模型之一，它能够以数学的形式来描述智能体在与环境交互的过程中学到一个目标的过程。

智能体充当的是作出决策或动作，并且在交互过程中学习的角色

环境指的是智能体与之交互的一切外在事物，不包括智能体本身。

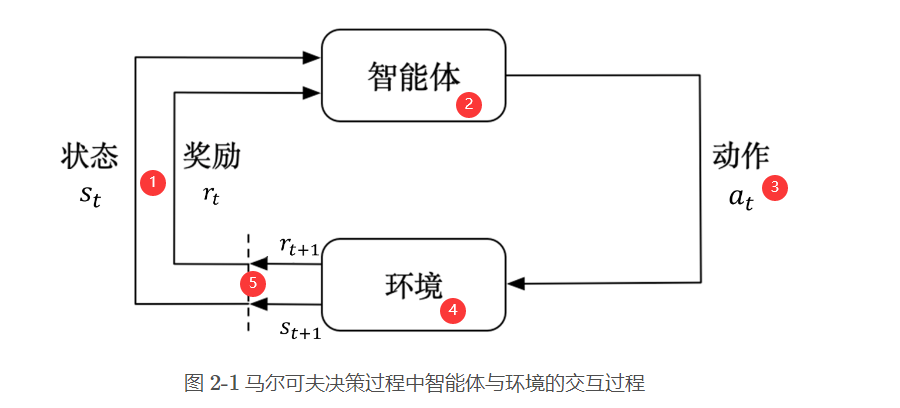
\qquad 确切地说，智能体与环境之间是在一系列离散的时步 ^①（ $\text{time?step}$ ）交互的，一般用 $t$ 来表示，$t=0,1,2,?$^②。在每个时步 $t$， 智能体会观测或者接收到当前环境的状态 $s_t$，根据这个状态 $s_t$ 执行动作 $a_t$。执行完动作之后会收到一个奖励 $r_{t+1}$ ^③，同时环境也会收到动作 $a_t$ 的影响会变成新的状态 $s_{t+1}$，并且在 $t+1$ 时步被智能体观测到。如此循环下去，我们就可以在这个交互过程中得到一串轨迹，如下式所示。
$$s_0,a_0,r_1,s_1,a_1,r_2,?,s_t,a_t,r_{t+1},?$$

以学习弹钢琴为例：
···
流程如下——学生根据老师的评价和琴声的反馈来更新自己演奏方式

智能体：学生
环境：钢琴和教师
动作：弹琴
状态：所弹琴键的位置顺序
奖励：钢琴的声音和教师的反馈
···
1.智能体接收上一步环境的状态和奖励
2.智能体做出动作与环境进行交互
3.更新环境的状态和奖励

基本概念

马尔可夫性质：某个状态的未来只与当前状态有关，与历史的状态无关。
$$P(s_{t+1}|s_t)=P(s_{t+1}|s_0,s_1,?,s_t)$$

马尔可夫决策过程中智能体的目标是最大化累积的奖励（回报），用 $G_t$ 表示，最简单的回报公式可以写成：

$$G_t=r_{t+1}+r_{t+2}+?+r_T$$

其中 $T$ 表示最后一个时步，也就是每回合的最大步数。

还有一种情况是智能体和环境持续交互，此时$T=\infty$，针对这种情况我们引入一个折扣因子（discount factor）$\gamma$，并可以将回报表示：

$$G_t=r_{t+1}+\gamma r_{t+2}+{\gamma }^2{r}_{t+3}+?=\sum _{k=0}^{T=\infty }{\gamma }^k{r}_{t+k+1}$$

其中$\gamma$ 取值范围在 $0$ 到 $1$ 之间，它表示了我们在考虑未来奖励时的重要程度，控制着当前奖励和未来奖励之间的权衡。换句话说，它体现了我们对长远目标的关注度。当 $\gamma =0$ 时，我们只会关心当前的奖励，而不会关心将来的任何奖励。而当 $\gamma$ 接近 $1$ 时，我们会对所有未来奖励都给予较高的关注度。

这样做的好处是会让当前时步的回报 $G_t$ 跟下一个时步 $G_{t+1}$ 的回报是有所关联的，我们可以得到递推式：

$$\begin{array}{rl}{G}_t& ?r_{t+1}+\gamma r_{t+2}+{\gamma }^2{r}_{t+3}+{\gamma }^3{r}_{t+4}+?\\ & =r_{t+1}+\gamma \left(r_{t+2}+\gamma r_{t+3}+{\gamma }^2{r}_{t+4}+?\right)\\ & =r_{t+1}+\gamma G_{t+1}\end{array}$$

状态转移矩阵是指在马尔可夫过程中，描述系统从一个状态到另一个状态的概率转移矩阵。

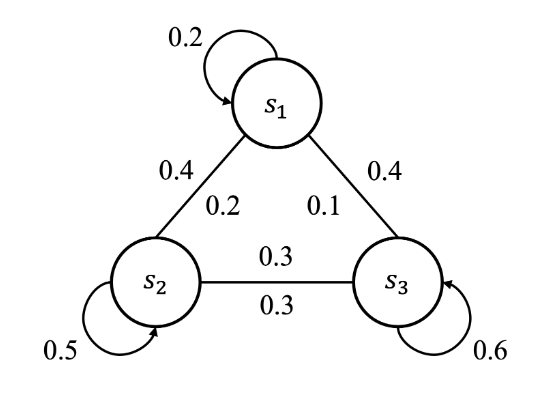
图中每个曲线箭头表示指向自己，比如当学生在认真听讲即处于状态 $s_1$ 时，会有 $0.2$ 的概率继续认真听讲。当然也会分别有 $0.4$ 和 $0.4$ 的概率玩手机（$s_2$）或者睡觉（$s_3$）。此外，当学生处于状态 $s_2$ 时，也会有 $0.2$ 的概率会到认真听讲的状态（$s_1$），像这种两个状态之间能互相切换的情况我们用一条没有箭头的线连接起来。

于状态数是有限的，我们可以把这些概率绘制成表格的形式：

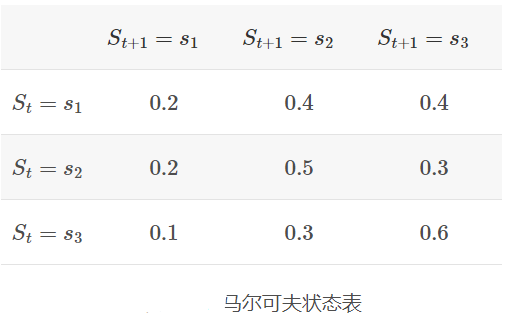
状态转移矩阵是环境的一部分，跟智能体是没什么关系的，而智能体会根据状态转移矩阵来做出决策。在马尔可夫链（马尔可夫过程）的基础上增加奖励元素就会形成马尔可夫奖励过程（Markov reward process, MRP）

练习

1. 强化学习所解决的问题一定要严格满足马尔可夫性质吗？请举例说明。

实际问题中，有很多例子其实是不符合马尔可夫性质的，比如我们所熟知的棋类游戏，因为在我们决策的过程中不仅需要考虑到当前棋子的位置和对手的情况，还需要考虑历史走子的位置例如吃子等。

2. 马尔可夫决策过程主要包含哪些要素？

MDP基于一组交互对象，即智能体和环境进行构建，所具有的要素包括状态、动作、策略和奖励

3. 马尔可夫决策过程与金融科学中的马尔可夫链有什么区别与联系？

$$马尔可夫链\stackrel{奖励元素}{?}马尔可夫奖励过程\stackrel{动作}{?}马尔可夫决策过程$$
在马尔可夫链（马尔可夫过程）的基础上增加奖励元素就会形成马尔可夫奖励过程（Markov reward process,MRP）， 在马尔可夫奖励过程基础上增加动作的元素就会形成马尔可夫决策过程，也就是强化学习的基本问题模型之一。
其中马尔可夫链和马尔可夫奖励过程在其他领域例如金融分析会用的比较多，强化学习则重在决策

DQN算法

算法定义

相比于Q learning，DQN本质上是为了适应更为复杂的环境，并且经过不断的改良迭代，到了Nature DQN（即Volodymyr Mnih发表的Nature论文）这里才算是基本完善。DQN主要改动的点有三个：

• 使用深度神经网络替代原来的Q表： ，Q表中我们描述状态空间的时候一般用的是状态个数，而在神经网络中我们用的是状态维度。例如在走迷宫问题中，神经网络只用了两个维度的输入就表示了原来 表中无穷多个状态，这就是神经网络的优势所在。
  

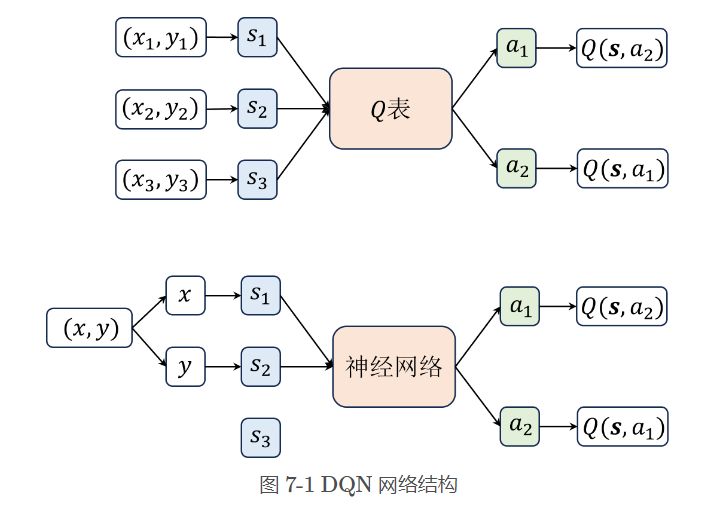
• 使用了经验回放（Replay Buffer）

  • 设计初衷：强化学习每次产生的样本之间是相互关联的 ， Q-learning算法训练的方式就是把每次通过与环境交互一次的样本直接喂入网络中训练。而在DQN中，我们会把每次与环境交互得到的样本都存储在一个经验回放中，然后每次从经验池中随机抽取一批样本来训练网络
    

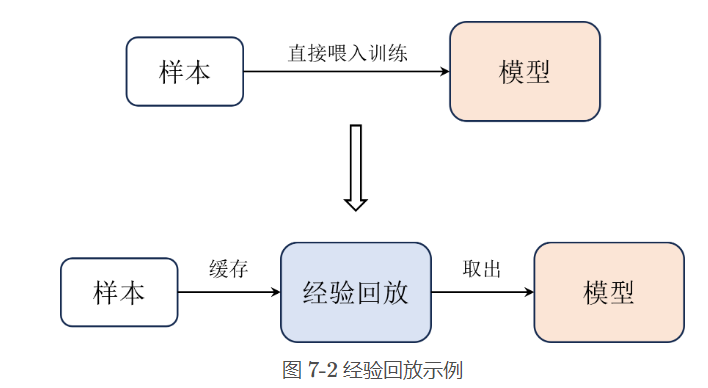
  • 使用一堆历史数据去训练，比之前用一次就扔掉好多了，大大提高样本效率

  • 减少样本之间的相关性，原则上获取经验跟学习阶段是分开的，原来时序的训练数据有可能是不稳定的，打乱之后再学习有助于提高训练的稳定性，跟深度学习中划分训练测试集时打乱样本是一个道理。

• 使用了两个网络：即策略网络和目标网络，每隔若干步才把每步更新的策略网络参数复制给目标网络，这样做也是为了训练的稳定，避免Q值的估计发散
  

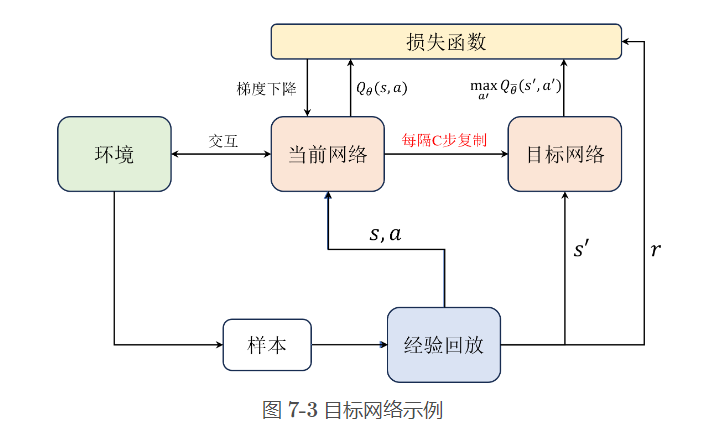
算法实现

算法伪代码

DQN代码实现

定义模型

首先是定义模型，就是定义两个神经网路，即当前网络和目标网络，它们的网络结构相同

class MLP(nn.Module): # 所有网络必须继承 nn.Module 类，这是 PyTorch 的特性
    def __init__(self, input_dim,output_dim,hidden_dim=128):
        super(MLP, self).__init__() 
        # 定义网络的层，这里都是线性层
        self.fc1 = nn.Linear(input_dim, hidden_dim) # 输入层
        self.fc2 = nn.Linear(hidden_dim,hidden_dim) # 隐藏层
        self.fc3 = nn.Linear(hidden_dim, output_dim) # 输出层
        
    def forward(self, x):
        # 各层对应的激活函数
        x = F.relu(self.fc1(x)) 
        x = F.relu(self.fc2(x))
        return self.fc3(x) # 输出层不需要激活函数

经验回放

经验回放的功能比较简单，主要实现缓存样本和取出样本等两个功能：

class ReplayBuffer:
    def __init__(self, capacity):
        self.capacity = capacity # 经验回放的容量
        self.buffer = [] # 用列表存放样本
        self.position = 0 # 样本下标，便于覆盖旧样本
    
    def push(self, state, action, reward, next_state, done):
        ''' 缓存样本
        '''
        if len(self.buffer) < self.capacity: # 如果样本数小于容量
            self.buffer.append(None)
        self.buffer[self.position] = (state, action, reward, next_state, done)
        self.position = (self.position + 1) % self.capacity 
    
    def sample(self, batch_size):
        ''' 取出样本，即采样
        '''
        batch = random.sample(self.buffer, batch_size) # 随机采出小批量转移
        state, action, reward, next_state, done =  zip(*batch) # 解压成状态，动作等
        return state, action, reward, next_state, done
    
    def __len__(self):
        ''' 返回当前样本数
        '''
        return len(self.buffer)

定义智能体

智能体即策略的载体，因此有的时候也会称为策略。智能体的主要功能就是根据当前状态输出动作和更新策略，分别跟伪代码中的交互采样和模型更新过程相对应。

import torch
import torch.optim as optim
import math
import numpy as np
class DQN:
    def __init__(self,model,memory,cfg):

        self.action_dim = cfg.action_dim  
        self.device = torch.device(cfg.device) 
        self.gamma = cfg.gamma # 奖励的折扣因子
        # e-greedy策略相关参数
        self.sample_count = 0  # 用于epsilon的衰减计数
        self.epsilon_start = cfg.epsilon_start
        self.epsilon_end =cfg.epsilon_end
        self.epsilon_decay = cfg.epsilon_decay
        self.batch_size = cfg.batch_size
        self.policy_net = model.to(self.device)
        self.target_net = model.to(self.device)
        # 复制参数到目标网络
        for target_param, param in zip(self.target_net.parameters(),self.policy_net.parameters()): 
            target_param.data.copy_(param.data)
        self.optimizer = optim.Adam(self.policy_net.parameters(), lr=cfg.lr) # 优化器
        self.memory = memory # 经验回放
    def sample_action(self, state):
        ''' 采样动作
        '''
        self.sample_count += 1
        # epsilon指数衰减
        self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \
            math.exp(-1. * self.sample_count / self.epsilon_decay) 
        if random.random() > self.epsilon:
            with torch.no_grad():
                state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
                q_values = self.policy_net(state)
                action = q_values.max(1)[1].item() # choose action corresponding to the maximum q value
        else:
            action = random.randrange(self.action_dim)
        return action
    @torch.no_grad() # 不计算梯度，该装饰器效果等同于with torch.no_grad()：
    def predict_action(self, state):
        ''' 预测动作
        '''
        state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
        q_values = self.policy_net(state)
        action = q_values.max(1)[1].item() # choose action corresponding to the maximum q value
        return action
    def update(self):
        if len(self.memory) < self.batch_size: # 当经验回放中不满足一个批量时，不更新策略
            return
        # 从经验回放中随机采样一个批量的转移(transition)
        state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(
            self.batch_size)
        # 将数据转换为tensor
        state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float)
        action_batch = torch.tensor(action_batch, device=self.device).unsqueeze(1)  
        reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float)  
        next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
        done_batch = torch.tensor(np.float32(done_batch), device=self.device)
        q_values = self.policy_net(state_batch).gather(dim=1, index=action_batch) # 计算当前状态(s_t,a)对应的Q(s_t, a)
        next_q_values = self.target_net(next_state_batch).max(1)[0].detach() # 计算下一时刻的状态(s_t_,a)对应的Q值
        # 计算期望的Q值，对于终止状态，此时done_batch[0]=1, 对应的expected_q_value等于reward
        expected_q_values = reward_batch + self.gamma * next_q_values * (1-done_batch)
        loss = nn.MSELoss()(q_values, expected_q_values.unsqueeze(1))  # 计算均方根损失
        # 优化更新模型
        self.optimizer.zero_grad()  
        loss.backward()
        # clip防止梯度爆炸
        for param in self.policy_net.parameters():  
            param.grad.data.clamp_(-1, 1)
        self.optimizer.step() 

环境定义

所以我们简单介绍一下该环境。环境名称叫做 推车杆游戏。如图 所示，我们的目标是持续左右推动保持倒立的杆一直不倒。

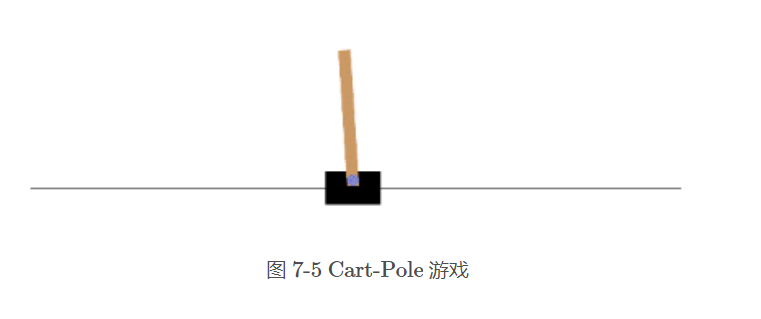
环境的状态数是4（推车的位置、速度、杆的角度、角速度） , 动作数是 2（倒、不倒）

import gymnasium as gym
import os
def all_seed(seed = 1):
    ''' 万能的seed函数
    '''
    if seed == 0: # 不设置seed
        return 
    np.random.seed(seed)
    random.seed(seed)
    torch.manual_seed(seed) # config for CPU
    torch.cuda.manual_seed(seed) # config for GPU
    os.environ['PYTHONHASHSEED'] = str(seed) # config for python scripts
    # config for cudnn
    torch.backends.cudnn.deterministic = True
    torch.backends.cudnn.benchmark = False
    torch.backends.cudnn.enabled = False
def env_agent_config(cfg):
    env = gym.make(cfg.env_id) # 创建环境
    all_seed(seed=cfg.seed)
    state_dim = env.observation_space.shape[0]
    action_dim = env.action_space.n
    print(f"状态空间维度：{state_dim}，动作空间维度：{action_dim}")
    setattr(cfg,"state_dim",state_dim) # 更新state_dim到cfg参数中
    setattr(cfg,"action_dim",action_dim) # 更新action_dim到cfg参数中
    model = MLP(state_dim, action_dim, hidden_dim = cfg.hidden_dim) # 创建模型
    memory = ReplayBuffer(cfg.memory_capacity)
    agent = DQN(model,memory,cfg)
    return env,agent

训练

参数设置：

self.epsilon_start = 0.95  # epsilon 起始值
self.epsilon_end = 0.01  # epsilon 终止值
self.epsilon_decay = 500  # epsilon 衰减率
self.gamma = 0.95  # 折扣因子
self.lr = 0.0001  # 学习率
self.buffer_size = 100000  # 经验回放容量（经验值）
self.batch_size = 64  # 批大小
self.target_update = 4  # 目标网络更新频率

训练函数：

def train(cfg, env, agent):
    ''' 训练
    '''
    print("开始训练！")
    rewards = []  # 记录所有回合的奖励
    steps = []
    for i_ep in range(cfg.train_eps):
        ep_reward = 0  # 记录一回合内的奖励
        ep_step = 0
        state, info = env.reset(seed = cfg.seed)  # 重置环境，返回初始状态
        for _ in range(cfg.max_steps):
            ep_step += 1
            action = agent.sample_action(state)  # 选择动作
            next_state, reward, terminated, truncated , info = env.step(action)  # 更新环境，返回transition
            agent.memory.push((state, action, reward, next_state, terminated))  # 保存transition
            state = next_state  # 更新下一个状态
            agent.update()  # 更新智能体
            ep_reward += reward  # 累加奖励
            if terminated:
                break
        if (i_ep + 1) % cfg.target_update == 0:  # 智能体目标网络更新
            agent.target_net.load_state_dict(agent.policy_net.state_dict())
        steps.append(ep_step)
        rewards.append(ep_reward)
        if (i_ep + 1) % 10 == 0:
            print(f"回合：{i_ep+1}/{cfg.train_eps}，奖励：{ep_reward:.2f}，Epislon：{agent.epsilon:.3f}")
    print("完成训练！")
    env.close()
    return {'rewards':rewards}

def test(cfg, env, agent):
    print("开始测试！")
    rewards = []  # 记录所有回合的奖励
    steps = []
    for i_ep in range(cfg.test_eps):
        ep_reward = 0  # 记录一回合内的奖励
        ep_step = 0
        state, info = env.reset(seed = cfg.seed)  # 重置环境，返回初始状态
        for _ in range(cfg.max_steps):
            ep_step+=1
            action = agent.predict_action(state)  # 选择动作
            next_state, reward, terminated, truncated , info = env.step(action)  # 更新环境，返回transition
            state = next_state  # 更新下一个状态
            ep_reward += reward  # 累加奖励
            if terminated:
                break
        steps.append(ep_step)
        rewards.append(ep_reward)
        print(f"回合：{i_ep+1}/{cfg.test_eps}，奖励：{ep_reward:.2f}")
    print("完成测试")
    env.close()
    return {'rewards':rewards}

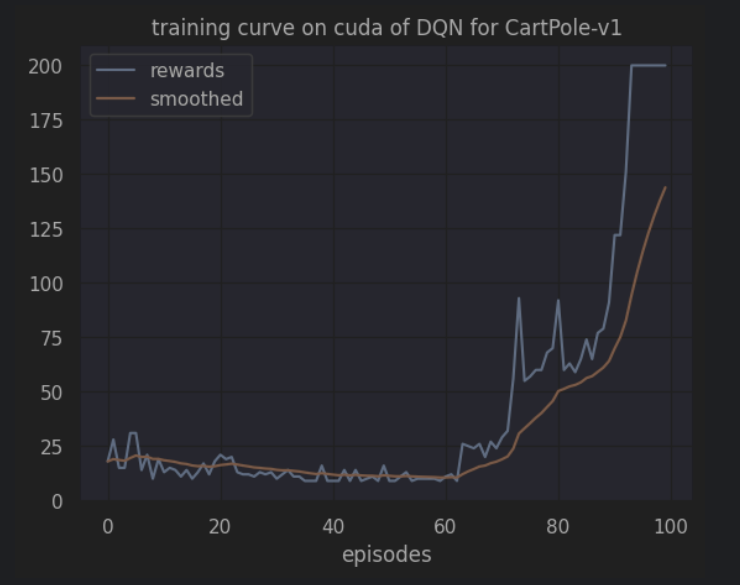
结果展示：

# 获取参数
cfg = Config() 
# 训练
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
 
plot_rewards(res_dic['rewards'], cfg, tag="train")  
# 测试
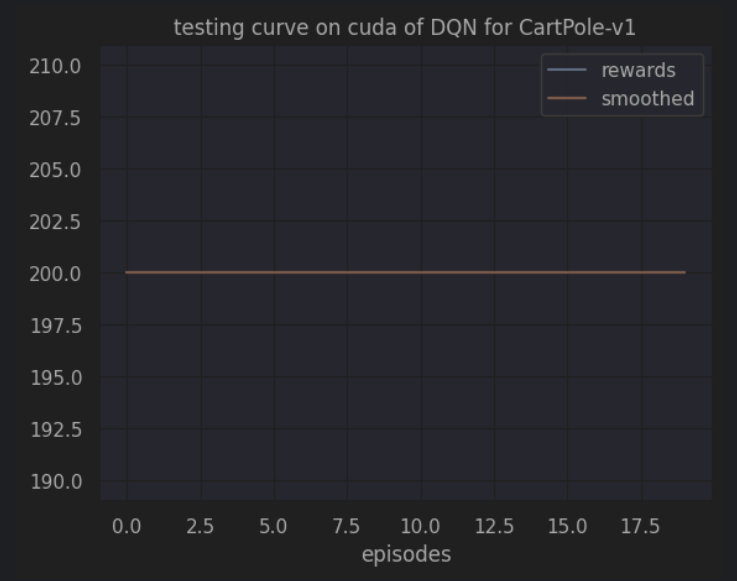
res_dic = test(cfg, env, agent)
plot_rewards(res_dic['rewards'], cfg, tag="test")  # 画出结果

状态空间维度：4，动作空间维度：2
开始训练！
回合：10/100，奖励：19.00，Epislon：0.638
回合：20/100，奖励：18.00，Epislon：0.487
回合：30/100，奖励：13.00，Epislon：0.366
回合：40/100，奖励：9.00，Epislon：0.296
回合：50/100，奖励：16.00，Epislon：0.239
回合：60/100，奖励：9.00，Epislon：0.198
回合：70/100，奖励：24.00，Epislon：0.135
回合：80/100，奖励：70.00，Epislon：0.049
回合：90/100，奖励：91.00，Epislon：0.019
回合：100/100，奖励：200.00，Epislon：0.010
完成训练！

开始测试！
回合：1/20，奖励：200.00
回合：2/20，奖励：200.00
回合：3/20，奖励：200.00
回合：4/20，奖励：200.00
回合：5/20，奖励：200.00
回合：6/20，奖励：200.00
回合：7/20，奖励：200.00
回合：8/20，奖励：200.00
回合：9/20，奖励：200.00
回合：10/20，奖励：200.00
回合：11/20，奖励：200.00
回合：12/20，奖励：200.00
回合：13/20，奖励：200.00
回合：14/20，奖励：200.00
回合：15/20，奖励：200.00
回合：16/20，奖励：200.00
回合：17/20，奖励：200.00
回合：18/20，奖励：200.00
回合：19/20，奖励：200.00
回合：20/20，奖励：200.00
完成测试

练习

1. 相比于$\text{Q-learning}$ 算法，$\text{DQN}$ 算法做了哪些改进？

1. 用深度网络代替 Q表，它的输入可以是连续的值，因此只需要把每个维度的坐标看作一个输入，就可以处理高维的状态空间了
2. Q-leanring算法训练的方式就是把每次通过与环境交互一次的样本直接喂入网络中训练。而在 DQN中，我们会把每次与环境交互得到的样本都存储在一个经验回放中，然后每次从经验池中随机抽取一批样本来训练网络

2. 为什么要在 $\text{DQN}$ 算法中引入 $\epsilon ?\text{greedy}$ 策略？

引入策略是为了平衡探索与利用的过程，如果智能体只进行利用，那么它可能会陷入局部最优，而忽略了更好的动作或状态；如果智能体只进行探索，那么它可能会浪费时间和资源，而无法收敛到最优的策略。因此，智能体需要在探索和利用之间进行权衡，以达到最佳的学习效果。

3. $\text{DQN}$ 算法为什么要多加一个目标网络？

在实践中每隔若干步才把每步更新的当前网络参数复制给目标网络，这样做的好处是保证训练的稳定，避免 Q 值的估计发散。

4. 经验回放的作用是什么？

首先每次迭代的样本都是从经验池中随机抽取的，因此每次迭代的样本都是近似独立同分布的，这样就满足了梯度下降法的假设。
其次，经验池中的样本是从环境中实时交互得到的，因此每次迭代的样本都是相互关联的，这样的方式相当于是把每次迭代的样本都进行了一个打乱的操作，这样也能够有效地避免训练的不稳定性。

DQN改进算法

Double DQN 算法

• Double DQN与Nature DQN的联系
  • 通过改进目标Q来优化算法
  • Nature DQN的第二个版本借鉴了Double DQN，采用两个网络
  • DQN的目标网络虽然也是定期更新的，但是它并不能完全解决过高估计的问题。这是因为，即使目标网络已经更新，选择最优动作的神经网络仍然可能会选择一个过高估计的动作，毕竟它们本来源自同一个权重，只不过稍有变化，所以会使得Q值过高。而Double DQN通过采用两个神经网络来估计Q值，可以减少这种情况的发生，从而提高智能体的表现。

class DoubleDQN(object):
    def __init__(self,cfg):
        self.states = cfg.n_states
        self.n_actions = cfg.n_actions  
        self.device = torch.device(cfg.device) 
        self.gamma = cfg.gamma  # 折扣因子
        # e-greedy策略相关参数
        self.sample_count = 0  # 用于epsilon的衰减计数
        self.epsilon = cfg.epsilon_start
        self.sample_count = 0  
        self.epsilon_start = cfg.epsilon_start
        self.epsilon_end = cfg.epsilon_end
        self.epsilon_decay = cfg.epsilon_decay
        self.batch_size = cfg.batch_size
        self.target_update = cfg.target_update
        self.policy_net = MLP(cfg.n_states,cfg.n_actions,hidden_dim=cfg.hidden_dim).to(self.device)
        self.target_net = MLP(cfg.n_states,cfg.n_actions,hidden_dim=cfg.hidden_dim).to(self.device)
         # 复制参数到目标网络
        for target_param, param in zip(self.target_net.parameters(),self.policy_net.parameters()): 
            target_param.data.copy_(param.data)
        # self.target_net.load_state_dict(self.policy_net.state_dict()) # or use this to copy parameters
        self.optimizer = optim.Adam(self.policy_net.parameters(), lr=cfg.lr)  # 优化器
        self.memory = ReplayBuffer(cfg.buffer_size) # 经验回放
        self.update_flag = False 

    def sample_action(self, state):
        ''' 采样动作
        '''
        self.sample_count += 1
        # epsilon指数衰减
        self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \
            math.exp(-1. * self.sample_count / self.epsilon_decay) 
        if random.random() > self.epsilon:
            with torch.no_grad():
                state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
                q_values = self.policy_net(state)
                action = q_values.max(1)[1].item() # choose action corresponding to the maximum q value
        else:
            action = random.randrange(self.n_actions)
        return action
    @torch.no_grad() # 不计算梯度，该装饰器效果等同于with torch.no_grad()：
    def predict_action(self, state):
        ''' 预测动作
        '''
        state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
        q_values = self.policy_net(state)
        action = q_values.max(1)[1].item() # choose action corresponding to the maximum q value
        return action
    def update(self):
        if len(self.memory) < self.batch_size: # 当经验回放中不满足一个批量时，不更新策略
            return
        else:
            if not self.update_flag:
                print("开始更新策略！")
                self.update_flag = True
        # 从经验回放中随机采样一个批量的转移(transition)
        state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(
            self.batch_size)
        # 将数据转换为tensor
        state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float)
        action_batch = torch.tensor(action_batch, device=self.device).unsqueeze(1)  
        reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float).unsqueeze(1)    
        next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
        done_batch = torch.tensor(np.float32(done_batch), device=self.device).unsqueeze(1)
        q_value_batch = self.policy_net(state_batch).gather(dim=1, index=action_batch) # 实际的Q值
        next_q_value_batch = self.policy_net(next_state_batch) # 下一个状态对应的实际策略网络Q值
        ##################################################################################
        next_target_value_batch = self.target_net(next_state_batch) # 下一个状态对应的目标网络Q值
        # 将策略网络Q值最大的动作对应的目标网络Q值作为期望的Q值
        next_target_q_value_batch = next_target_value_batch.gather(1, torch.max(next_q_value_batch, 1)[1].unsqueeze(1))
        expected_q_value_batch = reward_batch + self.gamma * next_target_q_value_batch* (1-done_batch) # 期望的Q值
        ##################################################################################
        # 计算损失
        loss = nn.MSELoss()(q_value_batch, expected_q_value_batch)
        # 优化更新模型
        self.optimizer.zero_grad()  
        loss.backward()
        # clip防止梯度爆炸
        for param in self.policy_net.parameters():  
            param.grad.data.clamp_(-1, 1)
        self.optimizer.step() 
        if self.sample_count % self.target_update == 0: # 每隔一段时间，将策略网络的参数复制到目标网络
            self.target_net.load_state_dict(self.policy_net.state_dict())   

Dueling DQN 算法

• Dueling DQN 算法通过优化神经网络的结构来优化算法的，在输出层之前分流，如图 所示，一个是优势层，用于估计每个动作带来的优势，输出维度为动作数，一个是价值层，用于估计每个状态的价值，输出维度为 1

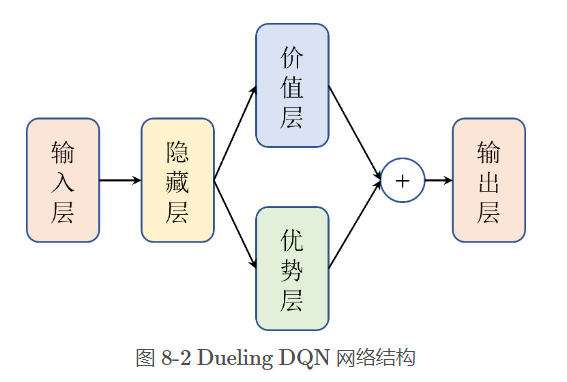
• 因为它分开评估每个状态的价值以及某个状态下采取某个动作的 值。当某个状态下采取一些动作对最终的回报都没有多大影响时，这个时候 这种结构的优越性就体现出来了。或者说，它使得目标值更容易计算，因为通过使用两个单独的网络，我们可以隔离每个网络输出上的影响，并且只更新适当的子网络，这有助于降低方差并提高学习鲁棒性。

import torch.nn as nn
import torch.nn.functional as F
class DuelingNet(nn.Module):
    def __init__(self, n_states, n_actions,hidden_dim=128):
        super(DuelingNet, self).__init__()
        
        # hidden layer
        self.hidden_layer = nn.Sequential(
            nn.Linear(n_states, hidden_dim),
            nn.ReLU()
        )
        
        #  advantage
        self.advantage_layer = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, n_actions)
        )
        
        # value
        self.value_layer = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, 1)
        )
        
    def forward(self, state):
        x = self.hidden_layer(state)
        advantage = self.advantage_layer(x)
        value     = self.value_layer(x)
        return value + advantage - advantage.mean()

Noisy DQN 算法

Noisy DQN算法也是通过优化网络结构的方法来提升DQN算法的性能，但与Dueling DQN算法不同的是，它的目的并不是为了提高Q值的估计，而是增强网络的探索能力。
在神经网络中引入了噪声层来提高网络性能的，即将随机性应用到神经网络中的参数或者说权重，增加了 网络对于状态和动作空间的探索能力，从而提高收敛速度和稳定性

import math
import torch
import torch.nn as nn
import torch.nn.functional as F
class NoisyLinear(nn.Module):
    def __init__(self, input_dim, output_dim, std_init=0.4):
        super(NoisyLinear, self).__init__()
        
        self.input_dim  = input_dim
        self.output_dim = output_dim
        self.std_init     = std_init
        
        self.weight_mu    = nn.Parameter(torch.FloatTensor(output_dim, input_dim))
        self.weight_sigma = nn.Parameter(torch.FloatTensor(output_dim, input_dim))
        self.register_buffer('weight_epsilon', torch.FloatTensor(output_dim, input_dim))
        
        self.bias_mu    = nn.Parameter(torch.FloatTensor(output_dim))
        self.bias_sigma = nn.Parameter(torch.FloatTensor(output_dim))
        self.register_buffer('bias_epsilon', torch.FloatTensor(output_dim))
        
        self.reset_parameters()
        self.reset_noise()
    
    def forward(self, x):
        if self.training: 
            weight = self.weight_mu + self.weight_sigma.mul(torch.tensor(self.weight_epsilon))
            bias   = self.bias_mu   + self.bias_sigma.mul(torch.tensor(self.bias_epsilon))
        else:
            weight = self.weight_mu
            bias   = self.bias_mu
        
        return F.linear(x, weight, bias)
    
    def reset_parameters(self):
        mu_range = 1 / math.sqrt(self.weight_mu.size(1))
        
        self.weight_mu.data.uniform_(-mu_range, mu_range)
        self.weight_sigma.data.fill_(self.std_init / math.sqrt(self.weight_sigma.size(1)))
        
        self.bias_mu.data.uniform_(-mu_range, mu_range)
        self.bias_sigma.data.fill_(self.std_init / math.sqrt(self.bias_sigma.size(0)))
    
    def reset_noise(self):
        epsilon_in  = self._scale_noise(self.input_dim)
        epsilon_out = self._scale_noise(self.output_dim)
        
        self.weight_epsilon.copy_(epsilon_out.ger(epsilon_in))
        self.bias_epsilon.copy_(self._scale_noise(self.output_dim))
    
    def _scale_noise(self, size):
        x = torch.randn(size)
        x = x.sign().mul(x.abs().sqrt())
        return x

class NoisyMLP(nn.Module):
    def __init__(self, input_dim,output_dim,hidden_dim=128):
        super(NoisyMLP, self).__init__()
        self.fc1 =  nn.Linear(input_dim, hidden_dim)
        self.noisy_fc2 = NoisyLinear(hidden_dim, hidden_dim)
        self.noisy_fc3 = NoisyLinear(hidden_dim, output_dim)
        
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.noisy_fc2(x))
        x = self.noisy_fc3(x)
        return x

    def reset_noise(self):
        self.noisy_fc2.reset_noise()
        self.noisy_fc3.reset_noise()

PER DQN 算法

优化了经验回放的设计从而提高模型的收敛能力和鲁棒性。PER 可以翻译为优先经验回放(prioritized experience replay)，跟数据结构中优先队列与普通队列一样,会在采样过程中赋予经验回放中样本的优先级。
TD误差越大，损失函数的值也越大，对于反向传播的作用也就越大。 。因此我们只需要设计一个经验回放，根据经验回放中的每个样本计算出的TD误差赋予对应的优先级，然后在采样的时候取出优先级较大的样本。

练习

1. DQN算法为什么会产生Q值的过估计问题?
   即使目标网络已经更新，选择最优动作的神经网络仍然可能会选择一个过高估计的动作，毕竟它们本来源自同一个权重，只不过稍有变化，所以会使得Q值过高。

2. 同样是提高探索，Noisy DQN与ε?greedy策略有什么区别
   深度强化学习既要考虑与环境交互过程中的探索能力，也要考虑深度模型本身的探索能力，从而尽量避免陷入局部最优解的困境之中，Noisy DQN是在神经网络的权重上添加参数化的噪音，从而使Q函数的输出具有随机性，而ε-greedy策略是在选择动作时以一定的概率随机选择一个动作，而不是最优的动作。同时Noisy DQN的探索是基于权重的，可以影响所有的动作的选择，而ε-greedy策略的探索是基于动作的，只影响单个的动作的选择。因此，Noisy DQN的探索更具有全局性和多样性，而ε-greedy策略的探索更具有局部性和随机性。

总结

本篇文章首先介绍了什么是强化学习，强化学习的作用以及应用场景。之后介绍了马尔可夫决策这一基本强化学习问题，了解了马尔可夫决策过程主要包含哪些要素，以及它和马尔可夫链之间的关系。之后我们学习了DQN算法，它首次将深度学习引入强化学习中，通过与Q-learning的对比介绍了DQN算法的基本流程以及代码实现。最后介绍了一些DQN算法的变种。