D36|背包问题

? ? ? ? 从图中我们可以看出背包问题主要涉及01背包、完全背包、多重背包和分组背包。?
01背包问题
1.暴力解法是一个回溯问题
2.动态规划方法涉及二维dp数组和一维dp数组解法,二维dp数组是1维dp数组的基础
二维dp数组解法:
首先考虑动态规划五部曲
1)dp数组的定义:
????????dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少
? ? ? ? 此处一定要注意i表示的是一个范围
2)递推公式:
?????????dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3)如何初始化:
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}也就是从容量大于weight[0]开始初始化到背包最大容量。
4)遍历顺序
????????先遍历 物品还是先遍历背包重量呢?
????????均可,先遍历物品更容易理解
// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
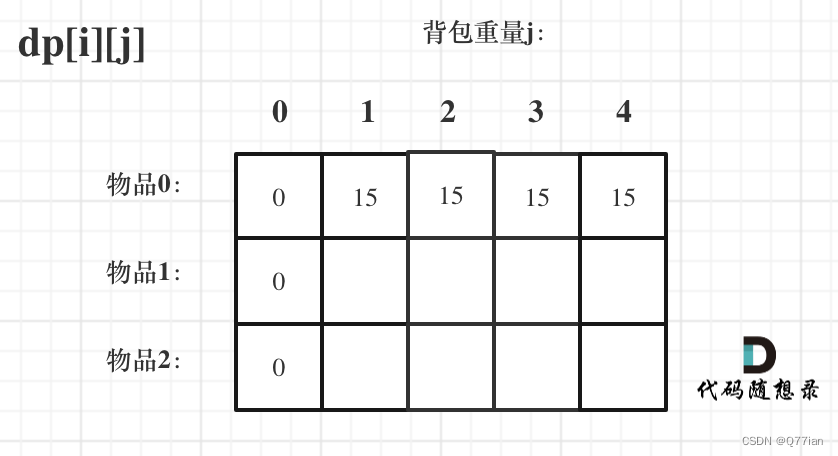
}5)举例推导递推数组。

卡码网46题
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int numofthings = sc.nextInt();
int weight = sc.nextInt();
int[] we = new int[numofthings];
int[] value = new int[numofthings];
for(int i = 0;i<numofthings;i++){
we[i] = sc.nextInt();
}
for(int i = 0;i<numofthings;i++){
value[i] = sc.nextInt();
}
// System.out.println("num"+numofthings);
// System.out.println("weight"+weight);
// System.out.println(Arrays.toString(we));
// System.out.println(Arrays.toString(value));
System.out.println(bagsolution(numofthings,weight,we,value));
}
public static int bagsolution(int num,int weight,int[] we,int[]value){
int[][] dp = new int[num][weight+1];
//初始化
for(int i = we[0];i<=weight;i++){
dp[0][i] = value[0];
}
//开始遍历
for(int i = 1;i<num;i++){
for(int j = 1;j<weight+1;j++){
if(we[i]>j){dp[i][j] = dp[i-1][j];}
else{
dp[i][j] = Math.max(dp[i-1][j],(dp[i-1][j-we[i]]+value[i]));
}
}
}
return dp[num-1][weight];
}
}?
一维DP数组解法(滚动数组):
动态规划五部曲:
1)dp数组的定义:
????????dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
2)递归公式:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);3)初始化:
?????dp数组初始化的时候,都初始为0。
4)遍历顺序:
? ? ? ? j是倒序遍历,保证每个物品只添加一次
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}?同时必须保证先遍历物品再遍历容量。
如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
比如在dp[4]中
dp[4] = Math.max(dp[4],dp[1]+value[1])此时,dp[1]还没有装入物品0,所以相当于仅放入了物品1.
5)举例推导dp数组
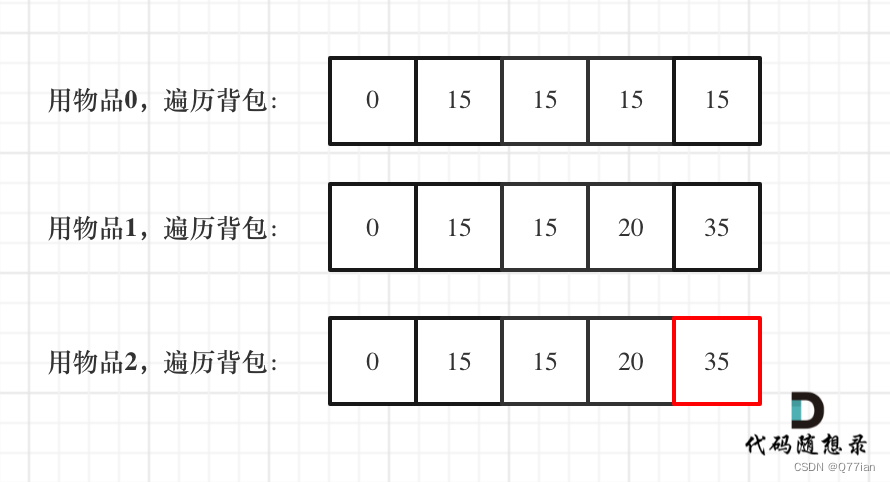
416.分割等和子集

初始思路:
首先求和,如果和/2是一个小数的话那么肯定不可分
然后就是联想,如何把该题转化为01背包问题呢?
物品 数组中的数
物品的重量 数组的值
物品的价值 数组的值
weight = sum/2;
如果在背包问题中有dp【j】 = weight;就代表可分
class Solution {
public boolean canPartition(int[] nums) {
double sum = 0;
for (int i = 0; i < nums.length; i++) {
sum = sum+ nums[i];
}
//System.out.println(sum);
double weight = sum/2;
//System.out.println(weight);
int integerPart = (int) weight; // 取整数部分
if (weight != integerPart) {
//System.out.println("该数是一个小数");
return false;
} else {
//System.out.println("该数不是一个小数");
int[] dp = new int[integerPart+1];
for(int i = 0;i<nums.length;i++){
for(int j=integerPart;j>=nums[i];j--){
dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);
if(dp[j]==integerPart){return true;}
}
}
}
return false;
}
}?题解复盘:
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
动规五部曲分析如下:
1.确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中每一个元素的数值既是重量,也是价值。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
2.确定递推公式
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
3.dp数组如何初始化
非0下标的元素初始化为0
4.确定遍历顺序
注意条件一定是j>=nums[i]!
// 开始 01背包
for(int i = 0; i < nums.size(); i++) {
for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
5.举例推导dp数组
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- springboot(ssm智慧生活商城系统 网上购物系统Java系统
- 23111 网络编程 day5
- MS31703NA,替代DRV8703,H 桥栅极驱动控制器
- 有关Quick BI中当返回值为空值,行标题消失问题
- Bifrost 中间件 X-Requested-With 系统身份认证绕过漏洞复现
- 【系统高级-环境变量】path配置一整行,而不是列表
- 浅谈基于深度学习的手写体纸质文档识别OCR软件
- BFC块级格式化上下文
- Java进阶 1-1 枚举
- cin.get()与cin.getline()的使用练习一题——平均绩点