蓝桥杯 归并排序 acwing版
上次题目答案
先公布一下上次内容的留的题目的答案吧,我相信看了并练习之后的人那个题目不成问题。
题目在上讲里面有,这里不再放出来了。
#include<iostream>
using namespace std;
bool check(int i){
for(int a = 1;a<=i;a++){
for(int b = 0;b < a;b++){
if(a*a-b*b==i){
return true;
}
}
}
return false;
}
int main(){
int ans = 0;
for(int i = 1;i <= 2021;i++){
if(check(i)){
ans++;
}
}
cout << ans;
return 0;
}答案:1516
分析:
n = a*a-b*bb的范围是(0,a)
a的范围是[1,n],为什么a至多能取到n呢?
? ? ? ? 以n=9为例:假设a=9,为了让a*a-b*b=9,就算b取最大值8,9*9-8*8仍然远大于9,所以a永远不会超过n(1例外)
下面开始讲解归并排序内容了:
1.归并排序介绍:
简单来说,我们可以说合并排序的过程是将数组分成两半,对每一半进行排序,然后将排序后的两半合并在一起。重复此过程,直到对整个数组进行排序。

2.动画展示过程
可以看出来现在不是跟之前一样一味的代数法了。其实代数法是为了能更好的理解函数递归的过程,除此之外无非就是验证程序的对错,所以还是希望大家能从本质上理解一个算法的思路,这样省时省力,我初学算法的时候就是一直不明白程序傻傻的老实想用代数法理解为什么这么写的,我现在的评价是大可不必,理解原理,模仿别人的写出代码,别跟自己过不去。不多bb了上内容。
合并排序是如何工作的?
合并排序是一种递归算法,它连续地将数组分成两半,直到无法进一步分割,即数组只剩下一个元素(具有一个元素的数组总是排序)。然后,将排序的子数组合并为一个排序的数组。
请参阅下图以了解合并排序的工作原理。
插图:
让我们考虑一个数组?arr[] = {38, 27, 43, 10}
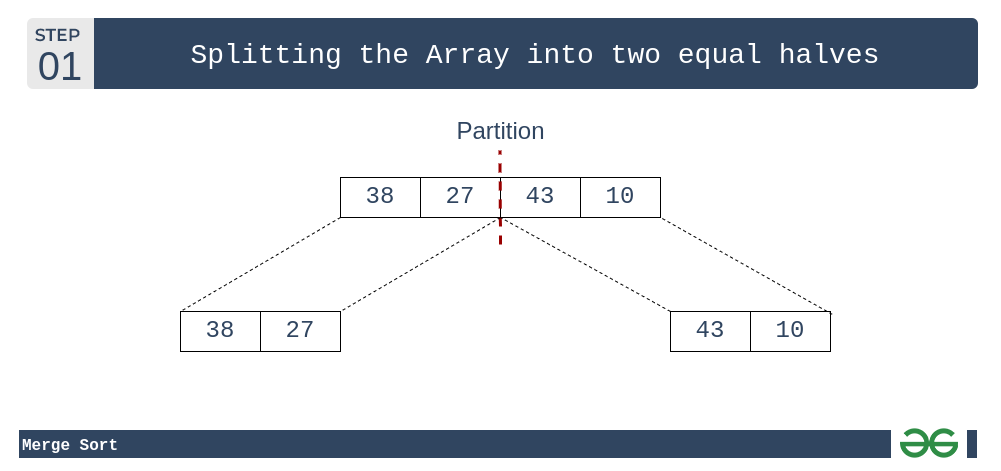
- 最初将数组分成相等的两半:
合并排序:将数组分成两半
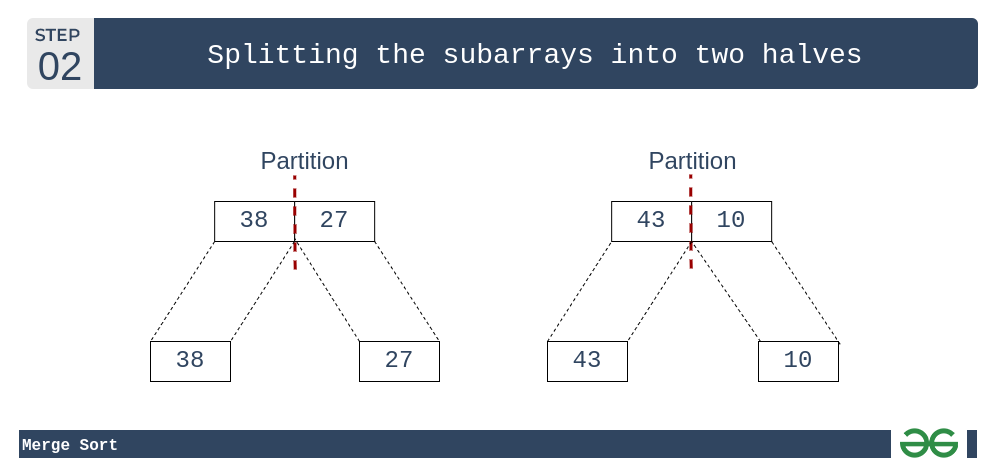
- 这些子阵列进一步分为两半。现在,它们成为无法再分割的单位长度数组,并且单位长度数组始终被排序。
合并排序:将子数组分成两半(此处为单位长度子数组)
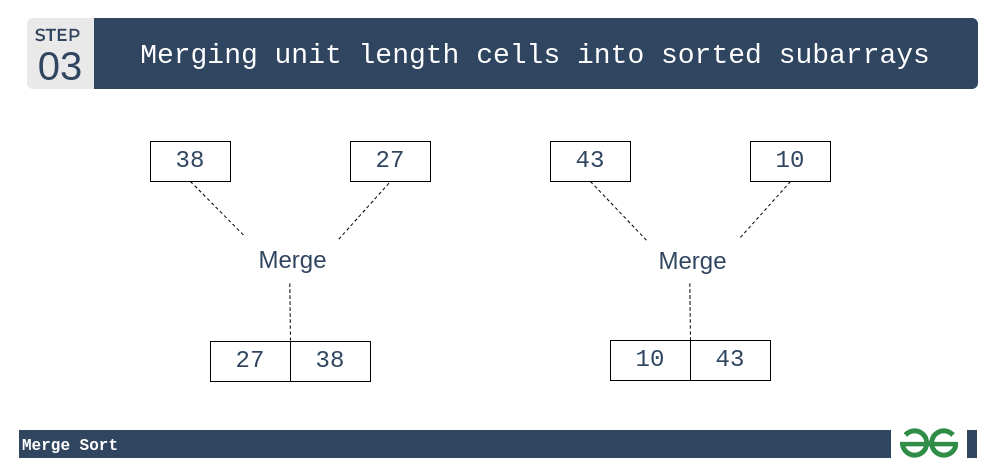
这些排序的子数组合并在一起,我们得到更大的排序子数组。
合并排序:将单位长度子数组合并到排序的子数组中
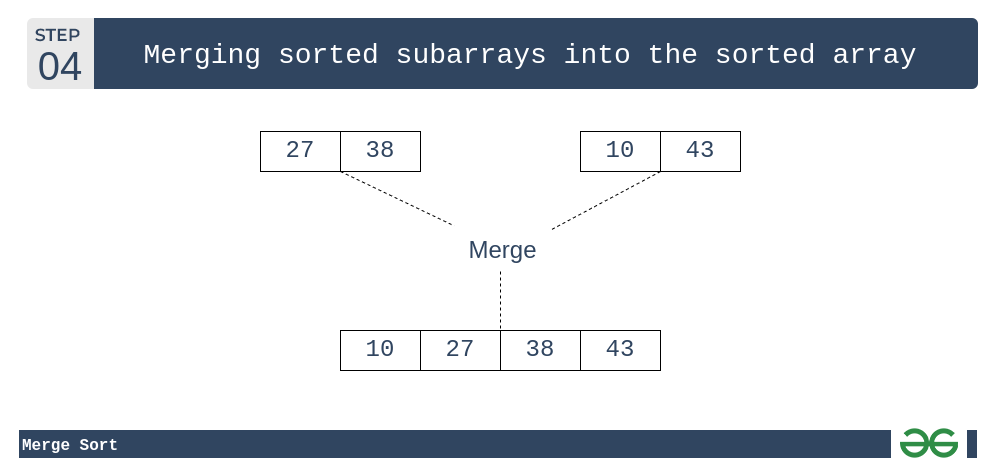
此合并过程将一直持续到从较小的子数组构建排序后的数组。
合并排序:合并排序后的子数组,得到排序后的数组
3.算法模板
void merge_sort(int q[], int l, int r) { //递归的终止情况 if(l >= r) return; //第一步:分成子问题 int mid = l + r >> 1; //第二步:递归处理子问题 merge_sort(q, l, mid ), merge_sort(q, mid + 1, r); //第三步:合并子问题 int k = 0, i = l, j = mid + 1, tmp[r - l + 1]; while(i <= mid && j <= r) if(q[i] <= q[j]) tmp[k++] = q[i++]; else tmp[k++] = q[j++]; while(i <= mid) tmp[k++] = q[i++]; while(j <= r) tmp[k++] = q[j++]; for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k]; }
4.讲解模板例题
讲算法模板
一个题目,这个题目也就是比模板多了传入数据的过程,也是便于大家更好的应用吧
题目:
给定你一个长度为?n?的整数数列。
请你使用归并排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式
输入共两行,第一行包含整数?n。
第二行包含?n?个整数(所有整数均在?1~1091~109?范围内),表示整个数列。
输出格式
输出共一行,包含?n个整数,表示排好序的数列。
数据范围
1≤n≤100000
输入样例:
5 3 1 2 4 5输出样例:
1 2 3 4 5
#include<iostream>
using namespace std;
const int N = 1000010;
int n;// 数组元素个数
int q[N];//待排序的数组
int tmp[N];// 用来存放合并左右两边结果的数组
void merge_sort()
{
// 当前区间只有一个数或者没有数
if(l>=r) return ;
// 确定分界点为数组中点
int mid = l+r>>1;
// 对左右两边进行递归排序
merge_sort(q,l,mid);
merge_sort(q,mid+1,r);
// 将左右两边排好序的部分合并
int k=0,i=l,j=mid+1;
while(i<=mid&&j<=r)
{
if(q[i]<=q[j])
{
tmp[k]=q[i];
k++;
i++;
}
else
{
tmp[k]=q[j];
k++;
j++;
}
}
//左半边有序数组没有循环完,剩余部分填到数组中
while(i<=mid)
{
tmp[k++]=q[i++];
}
// 右半边数组没有循环完,剩余部分填到数组中
while(j<=r)
{
tmp[k++]=q[j++];
}
for(i=l,j=0;i<=r;i++,j++)
{
q[i] = tmp[j];
}
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&q[i]);
}
merge_sort(q,0,n-1);
for(int i=0;i<n;i++)
{
printf("%d ",q[i]);
}
return 0;
}
- 确定分界点为中间位置,mid=(l+r)/2
- 递归排序左右两边
- 归并两个排好序的数组,合二为一(最难的部分),时间复杂度是O(n)
双指针算法
两个指针分别指向两个数组的开头,比较两个指针对应数值大小,小的放进新数组,该指针后移,直到一个指针到达数组末尾,将另外一个数组剩下的部分添加到新数组中。
1 3 5 7 9
2 4 5 8 10
i=0,j=0;p[i]=p[0]=1<q[j]=q[1]=2,s[0]=p[0]=1;i++;i=1,j=0;
i=1,j=0;p[i]=p[1]=3>q[j]=q[0]=2,s[1]=q[0]=2;j++;i=1,j=1;
i=1,j=1;p[i]=p[1]=3<q[j]=q[1]=4,s[2]=p[1]=3;i++;i=2,j=1;
i=2,j=1;p[i]=p[2]=5>q[j]=q[1]=4,s[3]=q[1]=4;j++;i=2,j=2;
i=2,j=2;p[i]=p[2]=5<=q[j]=q[2]=5,s[4]=p[2]=5;i++;i=3,j=2;
i=3,j=2;p[i]=p[3]=7>q[j]=q[2]=5,s[5]=q[2]=5;j++;i=3,j=3;
i=3,j=3;p[i]=p[3]=7<q[j]=q[3]=8,s[6]=p[3]=7,i++;i=4,j=3;
i=4,j=3;p[i]=p[4]=9>q[j]=q[3]=8,s[7]=q[3]=8,j++;i=4,j=4;
i=4,j=4;p[i]=p[4]=10>q[j]=q[4]=9,s[8]=q[4]=9,j++;i=4,j=5
s[9]=p[4]=10
原序列中两个值相同的数,排序后相对位置不发生变化。
5.习题
这里面我只找到了一个习题,给大家放出来吧,做练习,历年题没有,所以大家学习一下这个思想吧
题目描述:
给定一个长度为n的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i < j 且 a[i] > a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数n,表示数列的长度。
第二行包含 n 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000
输入样例:
6
2 3 4 5 6 1
输出样例:5
?分析:本题与AcWing 65 数组中的逆序对是同一题,再次写个题解以加深印象。
与归并排序类似,分而治之。
第一步:将原问题递归的划分为两个子问题L和R;
第二步:递归的求出子问题L和R中逆序对的个数;
第三步:合并子问题的解得到总问题的解。
唯一的问题在于子问题解的合并上,比如L上有x个逆序对,R上有y个逆序对,则LR上的逆序对并不是x与y简单的相加,还要加上两边的逆序对,比如L排好序后是1 3 5,R排好序后是2 4 6,L的排序消除了x个逆序对,R的排序消除了y个逆序对,此时原问题的状态变为1 3 5 2 4 6,可见还是有逆序对存在的,剩下的逆序对需要合并操作来消除。同样比较两个子问题指针指向元素的大小,1 < 2,1是最小的元素,不会存在逆序对,3 > 2,子问题L为1 3 5,既然3都大于2,则有序序列L 3右边的数也都必然大于2,所以L中大于2的数为L的右边界mid减去指向3的指针i加上1,即由2构成逆序对的数目。
本题代码只需在归并排序代码上稍作修改即可得到答案,总的代码如下:
代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 100005;
typedef long long ll;
int a[maxn], temp[maxn],n;
ll merge_sort(int *a, int l, int r) {
if (l >= r) return 0;
int mid = l + r >> 1;
ll res = merge_sort(a, l, mid) + merge_sort(a, mid + 1, r);
int k = 0,i = l,j = mid + 1;
while (i <= mid && j <= r) {
if (a[i] <= a[j]) temp[k++] = a[i++];
else
{
temp[k++] = a[j++];
res += mid - i + 1;
}
}
while (i <= mid) temp[k++] = a[i++];
while (j <= r) temp[k++] = a[j++];
for (i = l,j = 0; i <= r; i++,j++) a[i] = temp[j];
return res;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
printf("%lld\n", merge_sort(a, 0, n - 1));
return 0;
}6、浅谈时间复杂度、稳定性
O(nlogn)
归并排序是稳定的
如何看一个排序稳定不稳定?
一个排序算法是稳定的并不是说它的时间效率是稳定的。稳定是指如果原序列中的两个值相同的,经过排序之后,它们的位置没有发生变化,那么这个排序就是稳定的。它们的位置如果可能会发生变化,那么这个排序就是不稳定的。
?

那么明天见!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 等级保护的基本要求(一)
- 面试题:说一说多线程常见锁的策略 ?
- 94 使用快慢指针把有序链表转换为二叉搜索树
- ControlNet Adding Conditional Control to Text-to-Image Diffusion Models
- unity中0GC优化方案《zstring》
- dll不能运行是什么意思,分享5种有效的修复方法
- ElementPlus 国际化
- 一键汉字转拼音的方法,在线拼音转换,教你一键搞定
- 【产品经理】用户研究与需求分析
- 程序员必知!命令模式的实战应用与案例分析