【格密码】最近平面算法解决CVP问题（2）（完结篇）

目录

一. 铺垫

1.1 扩展空间

1.2 格基正交化

二. 与格点的距离

三. 最近平面算法定理

四. 小结

---

最近平面算法和CVP问题的基础解释，请先看这篇文章：

【格密码】最近平面算法解决CVP问题（1）-CSDN博客

一. 铺垫

1.1 扩展空间

令B代表格基。格的扩展空间通常写做span，代表格基向量的线性空间，如下：

第一个等号：代表 格的扩展空间与格基的扩展空间是一样的；

第二个等号：对格基B进行任意实数组合。

很显然，如果格基B为满秩的n阶方阵，那么格的扩展空间就是整个n维实数空间，写做

1.2 格基正交化

给定n个线性独立的向量，把它们转化成n个正交的向量，这个过程就是线性代数中所谓的Gram-Schmidt正交化过程。先来看一个二维向量的例子：

保持向量不变，也就是，将向量投影到向量的正交子空间上，就可以形成。

正交化的过程一般是按照顺序进行的，先，再接着一直往后。给定n个线性独立的向量，Gram-Schmidt正交化的计算公式如下：

注意j的取值代表i前面所有的向量，垂直于的分量即为。

向量的正交性告诉我们，对任意，都有：

空间维度保持不变告诉我们，可得：

注意向量正交化已经把格基改的面目全非，正交化后的格基已经不能形成原来的格点，看上面那张图就很清楚了。也就是向量不一定是格的格基。

通过正交化的公式不难看出，正交化的顺序很重要。给定n个线性独立的向量，其中每个向量都属于m维度，我们都知道标准正交基如下：

借助此理论，原始的格基可以表示为如下m行n列的矩阵：

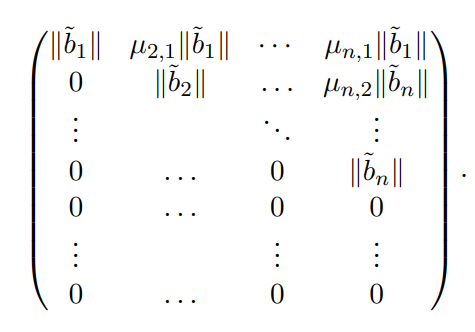
如果原始格满秩的话，也就是m=n，格基可以变成一个上三角的方阵。

二. 与格点的距离

给定任意的实数点t，满足：

最近平面算法的输出的格点离t肯定不会太远。根据上一篇文章（链接如上），每个维度上的距离向量都是介于以下之间：

假定x为最近平面算法输出的格点，该格点与向量t的距离肯定满足：

其中代表对格基列向量进行正交化。

根据LLL格基约化的性质，我们知道：

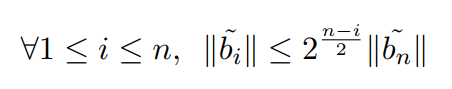
由此可得：

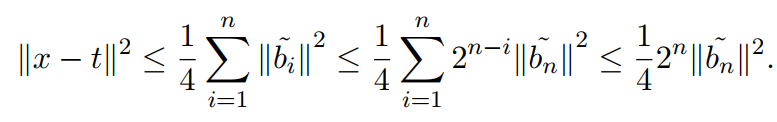
第一个不等号：最近平面算法的性质；

第二个不等号：LLL格基约化的性质；

第三个不等号：总小于1；

两边同时开平方，由此可得最近平面算法输出的格点距离，有一个上限，满足：

以上结果表明，当实数点到格点的距离满足：

此时最近平面算法的输出结果对应CVP的近似因子是。

三. 最近平面算法定理

给定任意实数点，令代表离其最近的格点。直接找出该格点是困难的，最近平面算法输出的格点为，满足：

证明：

代表最近平面算法输出的格点到实数点t的距离；

代表离实数点t最近的格点；

注意此时t可能不在格的扩展空间上，也就是：

此时我们把t可以投影到格的扩展空间上，称之为点s。已有的结论告诉我们：、

综合运算可得：

第一个等号：“超平面上的勾股定理”，向量s-t和向量s-x是垂直的

第一个不等号：最近平面算法的性质

第二个不等号：扩大了的系数

最后一个等号：超平面上的勾股定理；

两边开根号，进一步可得：

证明完毕

如果想提高最近平面算法的精度，则需要增加算法的时间复杂性。

四. 小结

计算机技术的快速发展， 使人们更加重视信息安全问题。 1976 年， Diffie 等人第一次提了公钥密码的概念， 这开启了现代密码学的新纪元。 在公钥密码体制中， 加密和解密不需要相同的密钥。网络安全大多数是基于一些数学难题， 如离散对数、 大整数分解。 但是， 1994 年， Peter Shor 提出来了一种量子算法， 可以在多项式时间内分解大整数，， 从而?RAS、 ELGgmma、 椭圆曲线（ ECC）等经典的加密算法将不再安全。

1996 年， Ajtai构建了一个单向函数族， 该函数族的安全性是基于格上的最坏情况复杂性问题， 并随之证明了攻破该单向函数就相当于能够解决格上的最坏情况复杂性问题。 这引起了密码学界的高度重视， 并提出了许多基于格上困难问题的密码学方案。 而且基于格上的加密方案使用到的计算只是整数矩阵向量乘法和模加法， 所以格上运算非常快捷。 而且， 格上的困难问题具有平均情况与最坏情况下的规约， 这使得基于格的方案很容易实例化， 而且能够抵抗量子计算机的攻击。 比如，在设计数字签名方案时， 我们可以选取任意一个随机的实例到挑战游戏中， 而不需要有意选择困难实例， 目前被证明有这一特性的密码体制只有格公钥密码。 基于格密码的理论优涉及网络安全的许多领域， 如云计算、 数据库、 密码学、 搜索引擎等。
但格上的签名空间尺寸大的缺点也是显而易见的。 比如我们想要描述一个 m 维的 q-ary 格， 我们必须构建一个m维的矩阵才能够清楚得把这个 m 维格的具体结构表达出来， 这需要非常大的空间， 从而影响了基于格的数字签名走向实用化。 为了解决上述问题，?多项式代数（NTRU） 格是一种高效的格。?随着数字签名方案的发展，?如盲签名、 群（环） 签名等也相继出现。?

一般情况下， 公钥密码方案的安全性可以规约到一些公认的传统数论问题的难解性上。 相似的， 格上的数字签名方案的安全性都可以规约到格上的困难问题， 目前， 已经证明了格上许多困难问题是 NP 困难。SVP 问题和 CVP 问题是格上两个最基本的计算难题。