数据结构之排序
发布时间：2023年12月20日
目录
一起去，更远的远方?
1.常见的排序算法
排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排 序算法是稳定的；否则称为不稳定的。
内部排序：数据元素全部放在内存中的排序。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。
?2.插入排序
直接插入排序
void InsertSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
int end = i - 1;
int tmp = a[i];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end+1] = a[end];
--end;
}
else
{
break;
}
}
a[end + 1] = tmp;
}
}
?
直接插入排序的特性总结：
1. 元素集合越接近有序，直接插入排序算法的时间效率越高
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)，它是一种稳定的排序算法
4. 稳定性：稳定?
希尔排序
希尔排序法又称缩小增量法。希尔排序法的基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后，取，重复上述分组和排序的工 作。当到达=1时，所有记录在统一组内排好序。
希尔排序的特性总结：
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。
3. 希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些树中给出的希尔排序的时间复杂度都不固定
?
当gap==1时就是直接插入排序，可以赋值对比一下
//希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end = end - gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
?
?希尔排序的时间复杂度我们直接记住一个结论? ?o(n^1.3)
3.交换排序
冒泡排序
前一个和后一个数循坏比较大的数字放最后面，然后再循环比剩下的数字
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
for (int i = 1; i < n-j; i++)
{
if (a[i-1] > a[i ])
{
int tmp = a[i];
a[i] = a[i -1];
a[i - 1] = tmp;
}
}
}
}
冒泡排序的特性总结：
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：稳定
快速排序
hoare版本
hoare排序思想： 我们默认序列左起第一个数为key，我们定义两个下标left和right分别从序列的左边和右边去找值，left找比key大的值，right找比key小的值，找到之后，交换left和right的值，等到left和right相遇的时候，此时的值一定是比key小的值，我们再把key和这个相遇位置的值进行交换，这样key就回到它应有的正确位置上，我们再递归处理key的左边区间和右边区间，递归结束之后，快排也就结束了。
//单趟排序，
int PartSort1(int* a, int left, int right)
{
int key = left;
while (left < right)
{
//左边做key，先走右边
while (left<right&& a[right] >= a[key])
{
right--;
}
//左边找大交换,找大的数，小的数就继续走，大的数是结束循环条件
while (left < right && a[left] <= a[key])
{
left++;
}
Swap(&a[left],&a[right]);
}
Swap(&a[key],&a[left]); //最后把key交换一下
return left;//相遇的位置，就是key中间的位置
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end) //当左边区间为空或者左边为1个就结束了
return;
int key = PartSort1(a, begin, end);
//begin key-1 key key+1 end
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}?
注意两个问题
a. 如果key后面的每个数都比key小或大的话，那left向后面找或right向前面找，就会产生越界访问的问题，为了防止这样情况的产生，我们选择在if语句的判断部分加个逻辑与&&保证left小于right，以免产生越界访问的问题。
b. 我们在if语句的判断部分，找的数一定得比key小或大，连相等都是不可以的，为什么呢？因为会产生死循环。
一旦序列中的左右出现相等的数字的时候，我们if语句如果写成＞或＜而不是>=或<=，程序就废了。
我们用的是分而治之的思想，第一趟排序找到了中间的key，然后再让begin，key-1和key+1,end再继续递归(begin，key-1,,,key,,,,,,key+1,end)
挖坑法
挖坑法思想： 挖坑法的思想还是要比hoare大佬的思想更加容易理解的，整体是一个什么思想呢？
我们先在序列的最左边挖一个坑，然后这个坑位的值就是key值，然后从右往左找比key小的值填到坑位上面去，这个时候坑位就变成right位置了，我们再从左向右找比key大的值，把这个值填到坑位上面去，再将坑位更新为left，循环进行这个工作，直到left和right相遇，他们相遇的位置也就是最后一次hole的位置，我们将key填到hole的位置，这样key就回到它本身的位置了。
剩下的工作我们还是交给递归，递归处理左区间和右区间。
?
//挖坑法
int PartSort1(int* a, int left, int right)
{
int key = a[left];
int hole = left;
while (left < right)
{
//先走右边
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
//左边找大交换,找大的数，小的数就继续走，大的数是结束循环条件
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return left;//相遇的位置，就是key中间的位置
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end) //当左边区间为空或者左边为1个就结束了
return;
int key = PartSort1(a, begin, end);
//begin key-1 key key+1 end
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
前后指针法
前后指针办法，这个简单方便
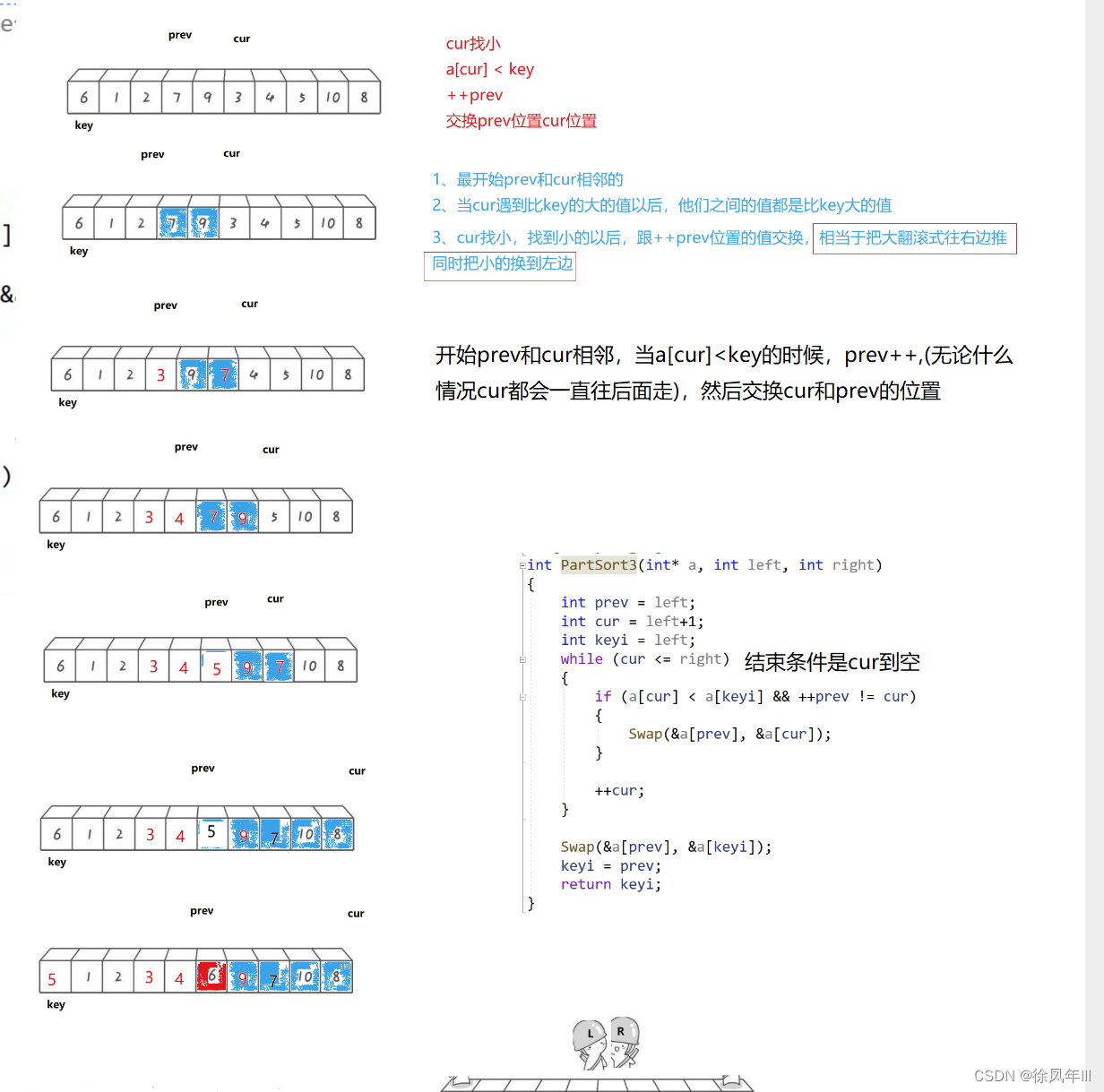
int PartSort3(int* a, int left, int right)
{
int prev = left;
int cur = left + 1;
int keyi = left;
while (cur<=right)
{
if (a[cur] < a[keyi])
{
prev++;
Swap(&a[cur],& a[prev]);
}
cur++;
}
Swap(&a[keyi], &a[prev]);
keyi = prev;
return keyi;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end) //当左边区间为空或者左边为1个就结束了
return;
int key = PartSort3(a, begin, end);
//begin key-1 key key+1 end
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(logN)
4. 稳定性：不稳定
?非递归实现
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
STInit(&st);
STPush(&st, end);
STPush(&st, begin);
while (!STEmpty(&st))
{
int left = STTop(&st);
STPop(&st);
int right = STTop(&st);
STPop(&st);
//int keyi = PartSort3(a, left, right);
int keyi = PartSort1(a, left, right);
// [left, keyi-1] keyi [keyi+1, right]
if (keyi + 1 < right)
{
STPush(&st, right);
STPush(&st, keyi + 1);
}
if (left < keyi-1)
{
STPush(&st, keyi-1);
STPush(&st, left);
}
}
STDestroy(&st);
}4.选择排序
直接选择排序
相当于玩扑克牌的时候，一把把全部的牌抓起来，按大小顺序排序
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int maxi = begin, mini = begin;
for (int i = begin; i <= end; i++)
{
if (a[i] > a[maxi])
{
maxi = i;
}
if (a[i] < a[mini])
{
mini = i;
}
}
Swap(&a[begin], &a[mini]);
if (begin == maxi)
{
maxi = mini;
}
Swap(&a[end], &a[maxi]);
++begin;
--end;
}
}
直接选择排序的特性总结：
1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定
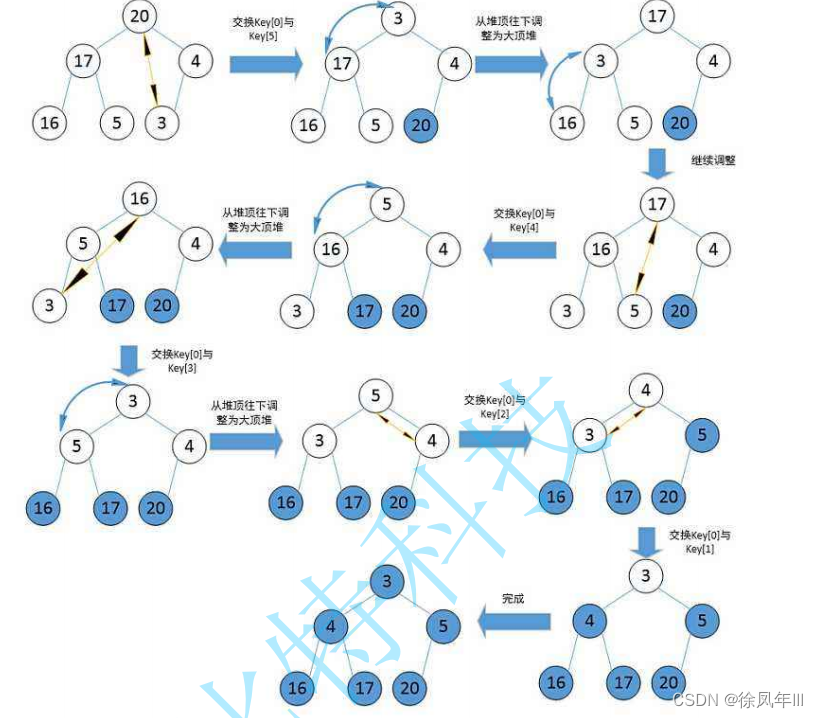
堆排序
向下调整算法
建堆+向下调整算法?
//向下调整
void AdjustDwon(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child < n)
{
//if (child + 1 < n && a[child + 1] < a[child]) //小堆
if (child + 1 < n && a[child + 1] > a[child]) //升序改成大堆
{
++child;
//默认左孩子最小，这样可以找出最小的那个孩子
}
//if (a[child] < a[parent]) //小堆是小于
if (a[child] > a[parent]) //大堆改成大于, 升序改成大堆
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排
//升序建大堆，降序建小堆
void HeapSort(int* a, int n)
{
//建堆，向下调整建堆
for (int i = (n - 1 - 1) / 2; i >=0; i--)
{
AdjustDwon(a,n,i);
}
int end = n - 1;
while (end > 0)
{
Swap(&a[end], &a[0]);
AdjustDwon(a, end, 0);
end--;
}
}详情可以看二叉树和堆的章节
堆排序
1. 堆排序使用堆来选数，效率就高了很多。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(1)
4. 稳定性：不稳定
5.归并排序
void _MergeSort(int* arr, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
_MergeSort(arr, begin, mid , tmp);
_MergeSort(arr, mid + 1, end, tmp);
int i = begin;
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] <= arr[begin2])//等于时我们取前一个，保证算法的稳定性
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
memcpy(arr+begin, tmp+begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* arr, int begin, int end)
{
int* tmp = (int*)malloc(sizeof(int) * (end - begin));
_MergeSort(arr, begin, end-1, tmp);
free(tmp);
tmp = NULL;
}
6.排序总结
文章来源:https://blog.csdn.net/m0_71920611/article/details/134901825
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 什么是云安全？如何保护云资源
- echarts 进度条类型柱状图
- prometheus federate ingesting out-of-order samples error
- RabbitMQ之延迟队列解读
- 智能助理助攻，办事效率翻倍 | 智能全链办2.0升级发布
- 【数据结构】排序之归并排序与计数排序
- 【NI-RIO入门】理解Windows、Real Time与FPGA之间数据通信的原理
- 6.3.3分离音频和视频
- CNC数控机床通过工业智能网关实现远程运维
- 深入了解TypeChat