代码+视频,手把手教你R语言使用forestploter包绘制单组及双组森林图
发布时间:2024年01月05日
森林图在论文中很常见,多用于表示多因素分析中的变量与结果变量的比值效应,可以用图示的方法比较直观的绘制出来。既往我们在文章《R语言快速绘制多因素回归分析森林图(1)》已经介绍了怎么绘制森林图,但是绘图比较简单,不够美观,不能绘制相对复杂的森林图。今天我们来介绍一下forestploter包,它等于是在forestplot包的基础上进一步强化功能,制作方法也相对简单一点,而且加强了对图形的精细控制,而且可以绘制单组和多组森林图。
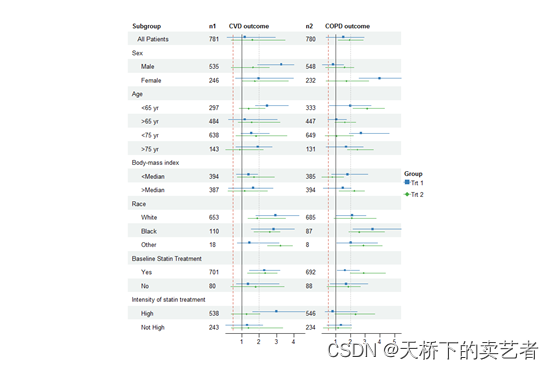
R语言使用forestploter包绘制单组及双组森林图
代码:
library(grid)
library(forestploter)
dt<-read.csv("E:/r/test/forest2.csv",sep=',',header=TRUE)
# 公众号回复:森林图数据2,可以获得数据
dt <- dt[,1:6]
#缩进一格
dt$Subgroup <- ifelse(is.na(dt$Placebo),
dt$Subgroup,
paste0(" ", dt$Subgroup))
#把治疗组和对照组NA(有缺失)的地方变成一个空格
dt$Treatment <- ifelse(is.na(dt$Treatment), "", dt$Treatment)
dt$Placebo <- ifelse(is.na(dt$Placebo), "", dt$Placebo)
#生成一个变量se,它在绘图的时候表示正方形的大小
dt$se <- (log(dt$hi) - log(dt$est))/1.96
#生成一个绘图区间,等下用来绘图
dt$` ` <- paste(rep(" ", 20), collapse = " ")
#生成HR和可信区间
dt$`HR (95% CI)` <- ifelse(is.na(dt$se), "",
sprintf("%.2f (%.2f to %.2f)",
dt$est, dt$low, dt$hi))#sprintF返回字符和可变量组合
#单组绘图
p <- forest(dt[,c(1:3, 8:9)],
est = dt$est, #效应值
lower = dt$low, #可信区间下限
upper = dt$hi, #可信区间上限
sizes = dt$se, #黑框的大小
ci_column = 4, #在那一列画森林图,要选空的那一列
ref_line = 1,
arrow_lab = c("Placebo Better", "Treatment Better"),
xlim = c(0, 4),
ticks_at = c(0.5, 1, 2, 3),
footnote = "This is the demo data. Please feel free to change\nanything you want.")
p
#没有P值怎么办,我们可以给它加上去
dt$p <- paste(rep("<0.05", 22))
p <- forest(dt[,c(1:3, 8:10)],
est = dt$est, #效应值
lower = dt$low, #可信区间下限
upper = dt$hi, #可信区间上限
sizes = dt$se, #黑框的大小
ci_column = 4, #在那一列画森林图,要选空的那一列
ref_line = 1,
arrow_lab = c("Placebo Better", "Treatment Better"),
xlim = c(0, 4),
ticks_at = c(0.5, 1, 2, 3),
footnote = "This is the demo data. Please feel free to change\nanything you want.")
p
#图形进行细节调整
dt_tmp <- rbind(dt[-1, ], dt[1, ])
dt_tmp[nrow(dt_tmp), 1] <- "Overall"
dt_tmp <- dt_tmp[1:11, ]
tm <- forest_theme(base_size = 10, #文本的大小
# Confidence interval point shape, line type/color/width
ci_pch = 15, #可信区间点的形状
ci_col = "#762a83", #CI的颜色
ci_fill = "blue", #ci颜色填充
ci_alpha = 0.8, #ci透明度
ci_lty = 1, #CI的线型
ci_lwd = 1.5, #CI的线宽
ci_Theight = 0.2, # Set an T end at the end of CI ci的高度,默认是NULL
# Reference line width/type/color 参考线默认的参数,中间的竖的虚线
refline_lwd = 1, #中间的竖的虚线
refline_lty = "dashed",
refline_col = "grey20",
# Vertical line width/type/color 垂直线宽/类型/颜色 可以添加一条额外的垂直线,如果没有就不显示
vertline_lwd = 1, #可以添加一条额外的垂直线,如果没有就不显示
vertline_lty = "dashed",
vertline_col = "grey20",
# Change summary color for filling and borders 更改填充和边框的摘要颜色
summary_fill = "yellow", #汇总部分大菱形的颜色
summary_col = "#4575b4",
# Footnote font size/face/color 脚注字体大小/字体/颜色
footnote_cex = 0.6,
footnote_fontface = "italic",
footnote_col = "red")
pt <- forest(dt_tmp[,c(1:3, 8:9)],
est = dt_tmp$est,
lower = dt_tmp$low,
upper = dt_tmp$hi,
sizes = dt_tmp$se,
is_summary = c(rep(FALSE, nrow(dt_tmp)-1), TRUE),
ci_column = 4,
ref_line = 1,
arrow_lab = c("Placebo Better", "Treatment Better"),
xlim = c(0, 4),
ticks_at = c(0.5, 1, 2, 3),
footnote = "This is the demo data. Please feel free to change\nanything you want.",
theme = tm)
pt
#多组的森林图
dt<-read.csv("E:/r/test/forest2.csv",sep=',',header=TRUE)
dt$Subgroup <- ifelse(is.na(dt$Placebo),
dt$Subgroup,
paste0(" ", dt$Subgroup))#######如果变量没有缺失,就缩进一格,也就是前进一格
#因为是双组变量,所以要设置2个n,这步和前面基本一样
dt$n1 <- ifelse(is.na(dt$Treatment), "", dt$Treatment)###将缺失的部分变为空格
dt$n2 <- ifelse(is.na(dt$Placebo), "", dt$Placebo)
#因为是要画两个森林图,所以要增加两个空地方来画图
dt$`CVD outcome` <- paste(rep(" ", 20), collapse = " ")
dt$`COPD outcome` <- paste(rep(" ", 20), collapse = " ")
#设置一些森林图的基本参数,这步和前面是一样的
tm <- forest_theme(base_size = 10,
refline_lty = "solid", #参考线类型
ci_pch = c(15, 18),
ci_col = c("#377eb8", "#4daf4a"),
footnote_col = "blue",
legend_name = "Group", #设置标题名字
legend_value = c("Trt 1", "Trt 2"), #设置分组名字
vertline_lty = c("dashed", "dotted"),
vertline_col = c("#d6604d", "#bababa"))
#最后绘图 ci_column = c(3, 5)是指在第3和5列绘图,est_gp1和est_gp2为一组,est_gp3和est_gp4为一组,其他的依次类推
p <- forest(dt[,c(1, 19, 21, 20, 22)],
est = list(dt$est_gp1,
dt$est_gp2,
dt$est_gp3,
dt$est_gp4),
lower = list(dt$low_gp1,
dt$low_gp2,
dt$low_gp3,
dt$low_gp4),
upper = list(dt$hi_gp1,
dt$hi_gp2,
dt$hi_gp3,
dt$hi_gp4),
ci_column = c(3, 5),
ref_line = 1,
vert_line = c(0.5, 2),
nudge_y = 0.2,
theme = tm)
p
文章来源:https://blog.csdn.net/dege857/article/details/135400624
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 设计模式-组合模式
- Web前端 ---- 【Vue】vue路由守卫(全局前置路由守卫、全局后置路由守卫、局部路由path守卫、局部路由component守卫)
- Mybatis——实现增删改查(详细操作)
- I2C总线和通信协议详解 (超详细配42张高清图+万字长文)
- 10分钟了解nextTick,并实现简易版本的nextTick
- 2024华数杯国际大学生数学建模A题思路+代码+模型+论文
- PYTHON基础:通过API收集GitHub上热门项目
- C++和Java中的随机函数你玩明白了吗?内附LeetCode470.rand7()爆改rand10()巨详细题解,带你打败LeetCode%99选手
- 自恢复保险丝
- 深入了解网络流量清洗--使用免费的雷池社区版进行防护