leetcode 013二维区域和检索---矩阵不可变

给定一个二维矩阵?matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的左上角为?(row1,?col1)?，右下角为?(row2,?col2)?。

实现?NumMatrix?类：

NumMatrix(int[][] matrix)?给定整数矩阵?matrix?进行初始化

int sumRegion(int row1, int col1, int row2, int col2)?返回左上角?(row1,?col1)?、右下角?(row2,?col2)?的子矩阵的元素总和。

示例 1：

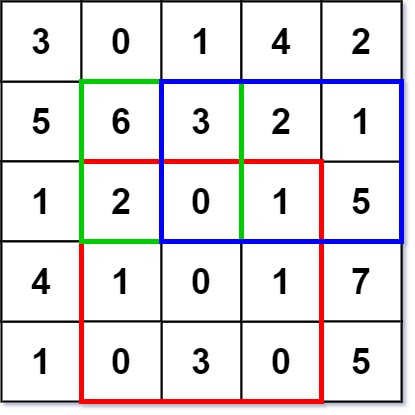
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

m == matrix.length

n == matrix[i].length

1 <= m,?n <=?200

-105?<= matrix[i][j] <= 105

0 <= row1 <= row2 < m

0 <= col1 <= col2 < n

最多调用?104?次?sumRegion?方法

解题思路：（前缀和思路）

对于一个二维矩阵，可能由于输入不同的坐标而反复求不同子矩阵的数字之和，所以需要尽可能快的实现子矩阵的数字求和

用前缀和的方式可快速求子矩阵的数字和

为了代码实现上方便，特意在最左边一列，最上边一列空出来

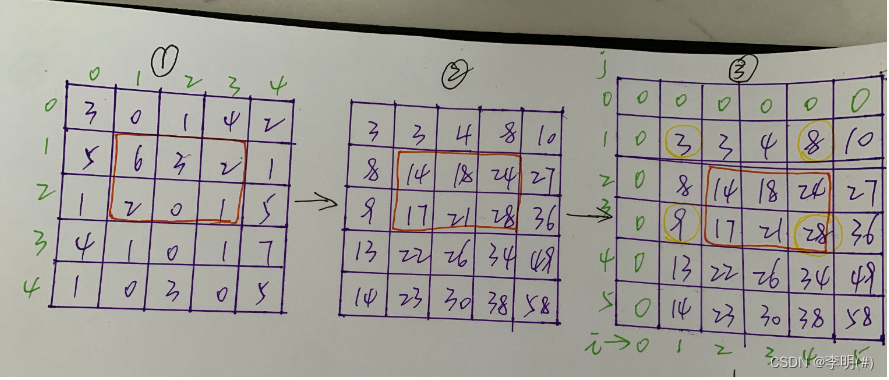
先根据原矩阵，求出前缀和矩阵，然后通过观察得知公式
sum[row2 + 1][col2 + 1] - sum[row1][col2 + 1] - sum[row2 + 1][col1] + sum[row1][col1]

class NumMatrix {
    int[][] sums;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        if (m > 0) {
            int n = matrix[0].length;
            sums = new int[m + 1][n + 1];
            for (int i = 0; i < m; i++) {
                for (int j = 0; j < n; j++) {
                    sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];
                }
            }
        }
    }
    
    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];
    }
}

此解题思路来自
https://leetcode.cn/problems/O4NDxx/solutions/1028794/jian-zhi-offer-zhuan-xiang-tu-po-ban-shu-5lks/
?