数据结构与算法教程，数据结构C语言版教程！（第四部分、字符串，数据结构中的串存储结构）三

第四部分、字符串，数据结构中的串存储结构

串存储结构，也就是存储字符串的数据结构。

很明显，字符串之间的逻辑关系也是“一对一”，用线性表的思维不难想出，串存储结构也有顺序存储和链式存储。

提到字符串，常做的操作就是串之间的匹配，因为，本章给初学者介绍 2 种串的模式匹配算法，BF 算法和 KMP 算法。

五、BF算法（串模式匹配算法）C语言详解

串的模式匹配算法，通俗地理解，是一种用来判断两个串之间是否具有"主串与子串"关系的算法。

主串与子串：如果串 A（如 "shujujiegou"）中包含有串 B（如 "ju"），则称串 A 为主串，串 B 为子串。主串与子串之间的关系可简单理解为一个串 "包含" 另一个串的关系。

实现串的模式匹配的算法主要有以下两种：

1. 普通的模式匹配算法；
2. 快速模式匹配算法；

本节，先来学习普通模式匹配（BF）算法的实现。

1、BF算法原理

普通模式匹配算法，其实现过程没有任何技巧，就是简单粗暴地拿一个串同另一个串中的字符一一比对，得到最终结果。

例如，使用普通模式匹配算法判断串 A（"abcac"）是否为串 B（"ababcabacabab"）子串的判断过程如下：

首先，将串 A 与串 B 的首字符对齐，然后逐个判断相对的字符是否相等，如图 1 所示：

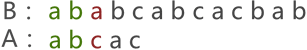
图 1 串的第一次模式匹配示意图

图 1 中，由于串 A 与串 B 的第 3 个字符匹配失败，因此需要将串 A 后移一个字符的位置，继续同串 B 匹配，如图 2 所示：

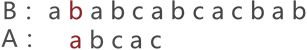
图 2 串的第二次模式匹配示意图

图 2 中可以看到，两串匹配失败，串 A 继续向后移动一个字符的位置，如图 3 所示：

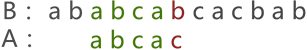
图 3 串的第三次模式匹配示意图

图 3 中，两串的模式匹配失败，串 A 继续移动，一直移动至图 4 的位置才匹配成功：

图 4 串模式匹配成功示意图

由此，串 A 与串 B 以供经历了 6 次匹配的过程才成功，通过整个模式匹配的过程，证明了串 A 是串 B 的子串（串 B 是串 A 的主串）。

接下来，我们要编写代码实现两个串的模式匹配（图 1 ~图 4）。

2、BF算法实现

BF 算法的实现思想是：将用户指定的两个串 A 和串 B，使用串的定长顺序存储结构存储起来，然后循环实现两个串的模式匹配过程，C 语言实现代码如下：

#include <stdio.h>

#include <string.h>

//串普通模式匹配算法的实现函数，其中 B是伪主串，A是伪子串

int mate(char * B,char *A){

????????int i=0,j=0;

????????while (i<strlen(B) && j<strlen(A)) {

????????????????if (B[i]==A[j]) {

????????????????????????i++;

????????????????????????j++;

????????????????}else{

????????????????????????i=i-j+1;

????????????????????????j=0;

????????????????}

????????}

????????//跳出循环有两种可能，i=strlen(B)说明已经遍历完主串，匹配失败；j=strlen(A),说明子串遍历完成，在主串中成功匹配

????????if (j==strlen(A)) {

????????????????return i-strlen(A)+1;

????????}

????????//运行到此，为i==strlen(B)的情况

????????return 0;

}

int main() {

????????int number=mate("ababcabcacbab", "abcac");

????????printf("%d",number);

????????return 0;

}

程序运行结果：

6

注意，在实现过程中，我们借助 i-strlen(A)+1 就可以得到成功模式匹配所用的次数，也就是串 A 移动的总次数。

2、BF算法时间复杂度时间复杂度

该算法最理想的时间复杂度?O(n)，n 表示串 A 的长度，即第一次匹配就成功。

BF 算法最坏情况的时间复杂度为?O(n*m)，n 为串 A 的长度，m 为串 B 的长度。例如，串 B 为 "0000000001"，而串 A 为 "01"，这种情况下，两个串每次匹配，都必须匹配至串 A 的最末尾才能判断匹配失败，因此运行了 n*m 次。

3、总结

BF 算法的实现过程很 "无脑"，不包含任何技巧，在对数据量大的串进行模式匹配时，算法的效率很低。

其实，BF 算法还可以改进，就是下节要学的 KMP 算法。

---

六、KMP算法（快速模式匹配算法）C语言详解

快速模式匹配算法，简称?KMP 算法，是在 BF 算法基础上改进得到的算法。学习 BF 算法我们知道，该算法的实现过程就是 "傻瓜式" 地用模式串（假定为子串的串）与主串中的字符一一匹配，算法执行效率不高。

KMP 算法不同，它的实现过程接近人为进行模式匹配的过程。例如，对主串 A（"ABCABCE"）和模式串 B（"ABCE"）进行模式匹配，如果人为去判断，仅需匹配两次。

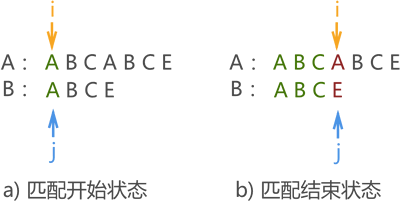
图 1 第一次人为模式匹配

第一次如图 1 所示，最终匹配失败。但在本次匹配过程中，我们可以获得一些信息，模式串中 "ABC" 都和主串对应的字符相同，但模式串中字符 'A' 与 'B' 和 'C' 不同。

因此进行下次模式匹配时，没有必要让串 B 中的 'A' 与主串中的字符 'B' 和 'C' 一一匹配（它们绝不可能相同），而是直接去匹配失败位置处的字符 'A' ，如图 2 所示：

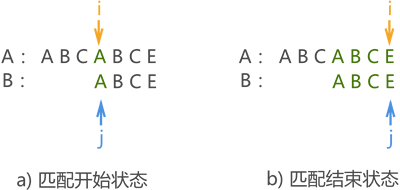
图 2 第二次人为模式匹配

至此，匹配成功。若使用 BF 算法，则此模式匹配过程需要进行 4 次。

由此可以看出，每次匹配失败后模式串移动的距离不一定是 1，某些情况下一次可移动多个位置，这就是 KMP 模式匹配算法。

那么，如何判断匹配失败后模式串向后移动的距离呢？

1、模式串移动距离的判断

每次模式匹配失败后，计算模式串向后移动的距离是 KMP 算法中的核心部分。

其实，匹配失败后模式串移动的距离和主串没有关系，只与模式串本身有关系。

例如，我们将前面的模式串 B 改为 "ABCAE"，则在第一次模式匹配失败，由于匹配失败位置模式串中字符 'E' 前面有两个字符 'A'，因此，第二次模式匹配应改为如图 3 所示的位置：

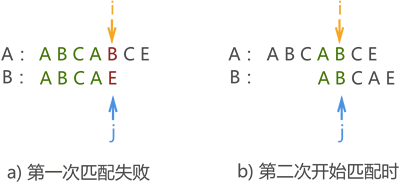
图 3 模式匹配过程示意图

结合图 1、图 2 和图 3 不难看出，模式串移动的距离只和自身有关系，和主串无关。换句话说，不论主串如何变换，只要给定模式串，则匹配失败后移动的距离就已经确定了。

不仅如此，模式串中任何一个字符都可能导致匹配失败，因此串中每个字符都应该对应一个数字，用来表示匹配失败后模式串移动的距离。

注意，这里要转换一下思想，模式串向后移动等价于指针 j 前移，如图 4 中的 a) 和 b)。换句话说，模式串后移相当于对指针 j 重定位。

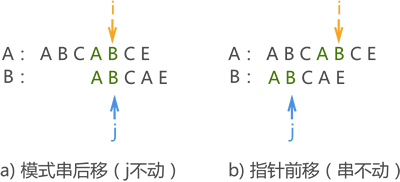
图 4 模式串后移等价于 j 前移

因此，我们可以给每个模式串配备一个数组（例如 next[]），用于存储模式串中每个字符对应指针 j 重定向的位置（也就是存储模式串的数组下标），比如 j=3，则该字符匹配失败后指针 j 指向模式串中第 3 个字符。

模式串中各字符对应 next 值的计算方式是，取该字符前面的字符串（不包含自己），其前缀字符串和后缀字符串相同字符的最大个数再 +1 就是该字符对应的 next 值。

前缀字符串指的是位于模式串起始位置的字符串，例如模式串 "ABCD"，则 "A"、"AB"、"ABC" 以及 "ABCD" 都属于前缀字符串；后缀字符串指的是位于串结尾处的字符串，还拿模式串 "ABCD" 来说，"D"、"CD"、"BCD" 和 "ABCD" 为后缀字符串。

注意，模式串中第一个字符对应的值为 0，第二个字符对应 1 ，这是固定不变的（先这么认为）。因此，图 3 的模式串 "ABCAE" 中，各字符对应的 next 值如图 5 所示：

图 5 模式串对应的 next 数组

从图 5 中的数据可以看出，当字符 'E' 匹配失败时，指针 j 指向模式串数组中第 2 个字符，即 'B'，同之前讲解的图 3 不谋而合。

以上所讲 next 数组的实现方式是为了让大家对此数组的功能有一个初步的认识。接下来学习如何用编程的思想实现 next 数组。编程实现 next 数组要解决的主要问题依然是 "如何计算每个字符前面前缀字符串和后缀字符串相同的个数"。

仔细观察图 5，为什么字符 'C' 对应的 next 值为 1？因为字符串 "AB" 前缀字符串和后缀字符串相等个数为 0，0 + 1 = 1。那么，为什么字符 'E' 的 next 值为 2？因为紧挨着该字符之前的 'A' 与模式串开头字符 'A' 相等，1 + 1 = 2。

如果图 5 中模式串为 "ABCABE"，则对应 next 数组应为 [0,1,1,1,2,3]，为什么字符 'E' 的 next 值是 3 ？因为紧挨着该字符前面的 "AB" 与开头的 "AB" 相等，2 + 1 =3。

因此，我们可以设计这样一个算法，刚开始时令 j 指向模式串中第 1 个字符（j=1），i 指向第 2 个字符（i=2）。接下来，对每个字符做如下操作：

如果 i 和 j 指向的字符相等，则 i 后面第一个字符的 next 值为 j+1，同时 i 和 j 做自加 1 操作，为求下一个字符的 next 值做准备，如图 6 所示：

图 6 i 和 j 指向字符相等

上图中可以看到，字符 'a' 的 next 值为 j +1 = 2，同时 i 和 j 都做了加 1 操作（此时 j=2，i=3）。当计算字符 'C' 的 next 值时，还是判断 i 和 j 指向的字符是否相等，显然相等，因此令该字符串的 next 值为 j + 1 = 3，同时 i 和 j 自加 1（此次 next 值的计算使用了上一次 j 的值）。如图 7 所示：

图 7 i 和 j 指向字符仍相等

如上图所示，计算字符 'd' 的 next 时，i 和 j 指向的字符不相等（此时 j=3，i=4），这表明最长的前缀字符串 "aaa" 和后缀字符串 "aac" 不相等，接下来要判断次长的前缀字符串 "aa" 和后缀字符串 "ac" 是否相等，这一步的实现可以用 j = next[j] 来实现（注意，next 数组从下标 1 开始使用，舍弃 next[0] ），如图 8 所示：

图 8 执行 j=next[j] 操作

从上图可以看到，i 和 j 指向的字符又不相同，因此继续做 j = next[j] 的操作，如图 9 所示：

图 9 继续执行 j=next[j] 的操作

此时，由于 j 和 i 指向的字符仍不相等，继续执行 j=next[j] 得到 j=0，这意味着字符 'd' 前的前缀字符串和后缀字符串相同个数为 0，因此如果字符 'd' 导致了模式匹配失败，则模式串移动的距离只能是 1。

这里给出使用上述思想实现 next 数组的 C 语言代码：

void Next(char*T,int *next){

????????next[1]=0;

????????int i=1;

????????int j=0;

????????//next[2]=1 可以通过第一次循环直接得出

????????while (i<strlen(T)) {

????????????????if (j==0||T[i-1]==T[j-1]) {

????????????????????????i++;

????????????????????????j++;

????????????????????????next[i]=j;

????????????????}else{

????????????????????????j=next[j];

????????????????}

????????}

}

代码中 j=next[j] 的运用可以这样理解，每个字符对应的next值都可以表示该字符前 "同后缀字符串相同的前缀字符串最后一个字符所在的位置"，因此在每次匹配失败后，都可以轻松找到次长前缀字符串的最后一个字符与该字符进行比较。

2、Next函数的缺陷

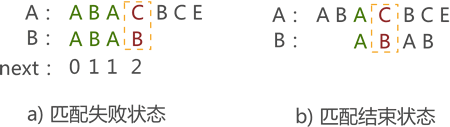
图 10 Next 函数的缺陷

例如，在图 10a) 中，当匹配失败时，Next 函数会由图 10b) 开始继续进行模式匹配，但是从图中可以看到，这样做是没有必要的，纯属浪费时间。

出现这种多余的操作，问题在当 T[i-1]==T[j-1] 成立时，没有继续对 i++ 和 j++ 后的 T[i-1] 和 T[j-1] 的值做判断。改进后的 Next 函数如下所示：

void Next(char*T,int *next){

????????next[1]=0;

????????int i=1;

????????int j=0;

????????while (i<strlen(T)) {

????????????????if (j==0||T[i-1]==T[j-1]) {

????????????????????????i++;

????????????????????????j++;

????????????????????????if (T[i-1]!=T[j-1]) {

????????????????????????????????next[i]=j;

????????????????????????}

????????????????????????else{

????????????????????????????????next[i]=next[j];

????????????????????????}

????????????????}else{

????????????????????????j=next[j];

????????????????}

????????}

}

注意，这里只设定了 next[1] 的值为 0，而 next[1] 的值，需要经过判断之后，才能最终得出，所以它的值不一定是 1。

使用精简过后的 next 数组在解决例如模式串为 "aaaaaaab" 这类的问题上，会大大提高效率，如图 11 所示，精简前为 next1，精简后为 next2：

图 11? 改进后的 Next 函数

3、KMP 算法的实现

假设主串 A 为 "ababcabcacbab"，模式串 B 为 "abcac"，则 KMP 算法执行过程为：

• 第一次匹配如图 12 所示，匹配结果失败，指针 j 移动至 next[j] 的位置；

  

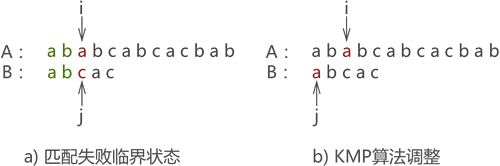
  图 12 第一次匹配示意图

• 第二次匹配如图 13 所示，匹配结果失败，依旧执行 j=next[j] 操作：

  

  图 13 第二次匹配示意图

• 第三次匹配成功，如图 14 所示：

  

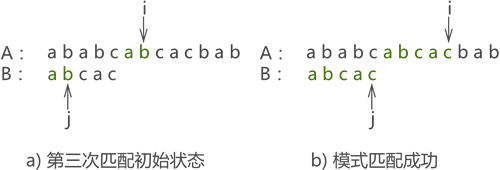
  图 14 第三次匹配示意图

很明显，使用 KMP 算法只需匹配 3 次，而同样的问题使用 BF 算法则需匹配 6 次才能完成。

KMP 算法的完整 C 语言实现代码为：

#include <stdio.h>

#include <string.h>

//调用了普通求 next 的方式，这里并未直接对 next[1] 赋值为 1，但通过函数第一次运行，也可以得出它的值为 1

void Next(char*T,int *next){

????????int i=1;

????????next[1]=0;

????????int j=0;

????????while (i<strlen(T)) {

????????????????if (j==0||T[i-1]==T[j-1]) {

????????????????????????i++;

????????????????????????j++;

????????????????????????next[i]=j;

????????????????}else{

????????????????????????j=next[j];

????????????????}

????????}

}

int KMP(char * S,char * T){

????????int next[10];

????????Next(T,next);//根据模式串T,初始化next数组

????????int i=1;

????????int j=1;

????????while (i<=strlen(S)&&j<=strlen(T)) {

????????????????//j==0:代表模式串的第一个字符就和当前测试的字符不相等；

????????????????S[i-1]==T[j-1],如果对应位置字符相等，两种情况下，指向当前测试的两个指针下标i和j都向后移

????????????????if (j==0 || S[i-1]==T[j-1]) {

????????????????????????i++;

????????????????????????j++;

????????????????} else{

????????????????????????j=next[j];//如果测试的两个字符不相等，i不动，j变为当前测试字符串的next值

????????????????}

????????}

????????if (j>strlen(T)) {//如果条件为真，说明匹配成功

????????????????return i-(int)strlen(T);

????????}

????????return -1;

}

int main() {

????????int i=KMP("ababcabcacbab","abcac");

????????printf("%d",i);

????????return 0;

}

运行结果为：

6

KMP 算法优秀文章推荐：

KMP算法推荐表

软文推荐	软文特点
KMP算法详解	此教程对KMP算法中 next 数组的实现做了详细地讲解，其实现代码与本文中有些出路，但两种实现都正确，只是出发点不同。
彻底理解KMP	此教程详细介绍了 BF算法和 KMP 算法，如果你能耐下心来读完，那么模式匹配算法肯定能彻底学会。
KMP算法	此页面中存在对 KMP 算法形象地描述，只不过是用 Java 语言实现，但是其理论知识的讲解堪称精彩。
KMP入门级算法详解	这篇软文对 KMP 算法的实现过程进行了最详细地描述，有图有真相，如果你阅读完本文，对 KMP 还是一知半解，可以看这篇文章。