手撕HashMap源码2
发布时间：2023年12月19日
目录
引言?
之前写了1，1里面重点讲了初始化过程，扩容过程，讲了一下链表的迁移等处理，今天这篇文章重点放在树化处理上，也就是红黑树，建议在阅读这篇文章之前，先去看我写的文章叫树之手撕红黑树，彻底理解红黑原理再来看才能看懂红黑树操作的部分，如果不想弄懂红黑树的操作部分，那就直接看代码逻辑
先从初始化一张表的时候来分析，初始化一张表，都会走进resize()这个方法里面，但是并不会涉及到树的操作，涉及到树的操作部分应该是我们在调用putVal方法的时候，当我们插入的数据在哈希表上面有相同的位置的时候，但是key不一样，就会在一个桶位形成链表或者红黑树
其实就是下面这个位置
当前插入的桶位结点如果是一棵红黑树的实例，那么就按照红黑树的方式进行数据的插入
现在我们先追进putTreeVal方法里面
putTreeVal红黑树添加结点方法讲解
/**
* Tree version of putVal.
* 红黑树插入结点的方法
* 参数1:第一个是当前结点HashMap对象
* 参数2：当前的哈希表
* 后面的结点依次是哈希值，键值
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
//确定键的可比较类，当哈希值无法直接参与比较大小的时候
//要通过这个参数去确定一下树里面是否存在一个相同的键，如果有就返回
Class<?> kc = null;
boolean searched = false;//是否已执行相同键的搜索
//获取树的根结点
TreeNode<K,V> root = (parent != null) ? root() : this;
//循环遍历树并插入新的键值对
for (TreeNode<K,V> p = root;;) {
int dir, ph; K pk;//方向值，哈希值，键值
//确定方向
//结点的哈希值大，走左边，说明当前传入的结点小
if ((ph = p.hash) > h)
dir = -1;
//结点的哈希值小，走右边，说明当前传入的结点大
else if (ph < h)
dir = 1;
//这里就是键已经存在，直接返回当前这个值就行了
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
//上面一条路都没干进去，哈希值没比较出来，键也没比较出来
//这里来说明一下comparableClassFor尝试获取键的可比较类，如果失败
//返回null ,说明这里键不是可比较的，如果是这种情况，内部调用find方法
//去查找是否有相同的键的存在，然后返回，避免重复插入
//另外一种情况是，如果键的可比较类kc存在,就通过compareComparables方法
//来比较键的大小，如果相等,dir返回0,内部还是调用find方法去找是否有相同的键值
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
//这里是红黑树出现键相等的情况时 ，选择插入的方向问题
dir = tieBreakOrder(k, pk);
}
//上面就给我们确定了方向，下面就是来放值
//将当前结点保存为父节点为xp
TreeNode<K,V> xp = p;
//左边，或者右边有位置才会进来放值
//一般在叶子结点，或者倒数第二层结点来放值，并把左边或者右边结点交给p来进行轮替
if ((p = (dir <= 0) ? p.left : p.right) == null) {
//创建一个新的树结点
Node<K,V> xpn = xp.next;//保留next指针
//添加了一个指向父亲的next指针xpn
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
//连接上新结点x
if (dir <= 0)
xp.left = x;
else
xp.right = x;
//父亲的next指向了新的结点x
xp.next = x;
x.parent = x.prev = xp;
if (xpn != null)
//既然x的next是指向了xpn,那么xpn的prev就指向了x
//这里的指向都是考虑为链表的next与prev
((TreeNode<K,V>)xpn).prev = x;
//插入后调整树的结构，将根结点放在桶位上，也就是链表的表头
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}treeifyBin进行树化的方法（虚假的树化）
/**
* Replaces all linked nodes in bin at index for given hash unless
* table is too small, in which case resizes instead.
* 将给定哈希值对应的索引处的链表结构转化为树结构
* 除非哈希表过小，此时会选择进行扩容而不是树化
*/
final void treeifyBin(Node<K,V>[] tab, int hash) {
//e是临时变量，用于遍历链表中的结点
int n, index; Node<K,V> e;//n表示哈希表的长度，index表示计算出的索引
//之前说了，一个桶位它是否进行树化，首先取决于
//当前哈希表的元素是否大于默认值，也就是MIN_TREEIFY_CAPACITY
//也就是是否大于64,小于64，不树化，直接进行扩容处理
//所以这里其实也涉及到一个问题，当我们在对数据插入的时候，第一次在一个桶位上形成树是在什么时候
//在数据进行putVal的时候，最开始的数据进来，有重复的索引位置
//刚开始的时候肯定会形成链表，当这个桶位的结点数目的阈值大于了TREEIFY_THRESHOLD,
//也就是8的时候，他会进入这个树化方法，也就是treeifyBin这个方法
//当进入这个方法之后，他还会去判定整个链表的数据有没有达到64，如果没有达到64
//就按照扩容进行处理
//所以第一次形成一棵树的条件是，首先整张表的数据要达到64,其次链表里面的结点数目必须大于等于8
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
//那么这条路线肯定满足了树化的条件
//注意这个点的这条路线已经在走链表了
//这里判断其实多余，因为在putVal里面已经做了一次判断
//下面就是把链表进行树化
else if ((e = tab[index = (n - 1) & hash]) != null) {
//定义一个树的头结点和树的尾结点
TreeNode<K,V> hd = null, tl = null;
//其实这里的循环就干了一件事儿，把每一个链表的结点
//变成一棵树的结点，并且把树里面的prev与next指针按照链表的指向链接上
do {
//把每一个链表结点替换成树结点
TreeNode<K,V> p = replacementTreeNode(e, null);
//下
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);//循环遍历整个链表
//下面是变成一棵真正的红黑树结构
//并且将转化为树的头结点放回哈希表中
if ((tab[index] = hd) != null)
hd.treeify(tab);//真正树化操作
}
}treeify真正的树化操作
/**
* Forms tree of the nodes linked from this node.
* 进行树化的操作
* 参数是一个哈希表
* 这里是真正把left与right节点给挂上了
*/
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
//x：拿到当前结点初始值
//遍历整棵树的结点,this是拿到当前这个树结结点
//其实这个操作就是整体循环了一遍链表
for (TreeNode<K,V> x = this, next; x != null; x = next) {
//获取当前结点的下一个结点
next = (TreeNode<K,V>)x.next;
//把当前结点左右结点都指向null，挂空
x.left = x.right = null;
//如果当前红黑树的根结点为空的时候，就把x变为根结点，颜色变黑
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
else {
//获取插入结点的k值
K k = x.key;
//插入结点的hash值
int h = x.hash;
Class<?> kc = null;
//从根结点开始遍历
for (TreeNode<K,V> p = root;;) {
int dir, ph;//dir:标记下个结点的方向 ph:当前结点的hash值
K pk = p.key;//当前结点的key值
//如果当前插入结点的hash值小于当前结点的hash值，下次查找向左查找
if ((ph = p.hash) > h)
dir = -1;
//另外就是向右查找
else if (ph < h)
dir = 1;
//如果上面都没比较出来，走下面的方法
//或者jdk自带的方法进行比较
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0)
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;//保留当前p结点
//如果p结点左右有位值，也就是左边或者右边等于null的情况，就开始挂结点
//如果左右都有结点，不等于null,然后往下面走
if ((p = (dir <= 0) ? p.left : p.right) == null) {
//x的父亲指向p
x.parent = xp;
//根据方向来挂结点
if (dir <= 0)
xp.left = x;
else
xp.right = x;
//调整平衡
root = balanceInsertion(root, x);
break;
}
}
}
}
//把头结点放到表的头部
moveRootToFront(tab, root);
}上面就是整个表第一次会在一个桶位形成红黑树的分析。
从扩容的部分来分析红黑树的代码
如果发现这个节点是一个红黑树的结点，就会按照红黑树的方式进行结点的迁移
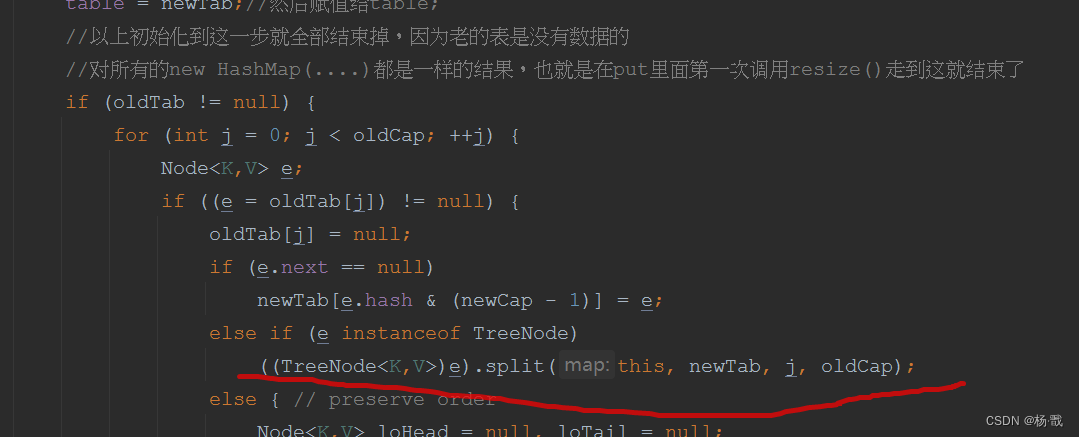
?那么我们追进去看一下split
split红黑树扩容迁移的方法
/**
* Splits nodes in a tree bin into lower and upper tree bins,
* or untreeifies if now too small. Called only from resize;
* see above discussion about split bits and indices.
*
* @param map the map
* @param tab the table for recording bin heads
* @param index the index of the table being split
* @param bit the bit of hash to split on
* 对几个参数做一些说明
* 第一个参数是当前哈希map对象
* 第二个参数是新的表
* 第三个参数是当前表第一个结点在表里面的索引
* 第四个参数是原来表的长度
*/
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
TreeNode<K,V> b = this;//当前hash桶下标所在的第一个结点
// Relink into lo and hi lists, preserving order
//还是分为低位链表与高位链表来处理1
TreeNode<K,V> loHead = null, loTail = null;
TreeNode<K,V> hiHead = null, hiTail = null;
int lc = 0, hc = 0;//这里是高位表和低位表的计数
//把当前结点交给e
//还定义了一个中间结点next
for (TreeNode<K,V> e = b, next; e != null; e = next) {
next = (TreeNode<K,V>)e.next;//把下一个结点交给next,每次一次循环完，在把next交给e
//把当前结点的next给挂空，因为已经交给next了
e.next = null;
//还是与原来的长度&，高位为0还是低链表
//大体和链表的处理方式一样，只是这里有一个prev指针指向前面的一个结点
if ((e.hash & bit) == 0) {
if ((e.prev = loTail) == null)//这里的e.prev是给了一个指向前面结点的指针
loHead = e;//第一次loHead指向第一个结点
else
loTail.next = e;
loTail = e;
++lc;
}
else {
if ((e.prev = hiTail) == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
++hc;
}
}
//循环完了之后
//下面就是判断进行树化还是不树化
if (loHead != null) {
//如果小于6，就退树成链
if (lc <= UNTREEIFY_THRESHOLD)
tab[index] = loHead.untreeify(map);//还是按照链表的方式处理
else {
tab[index] = loHead;
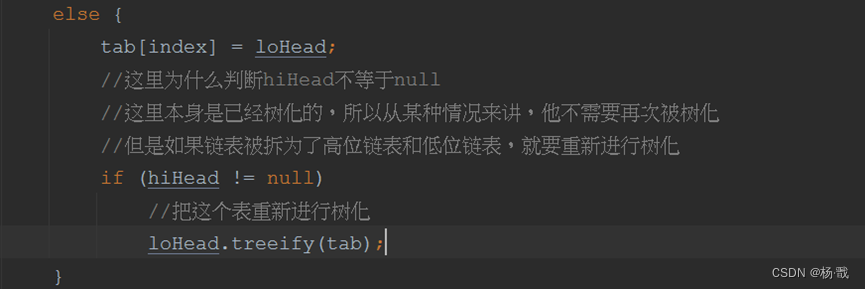
//这里为什么判断hiHead不等于null
//这里本身是已经树化的，所以从某种情况来讲，他不需要再次被树化
//但是如果链表被拆为了高位链表和低位链表，就要重新进行树化
if (hiHead != null)
//把这个表重新进行树化
loHead.treeify(tab);
}
}
//同样的处理方式
if (hiHead != null) {
if (hc <= UNTREEIFY_THRESHOLD)
tab[index + bit] = hiHead.untreeify(map);
else {
tab[index + bit] = hiHead;
if (loHead != null)
hiHead.treeify(tab);
}
}
}我们去注意一下下面这个位置
这个位置就是退树成链的方法，当高位结点或者低位结点里面的链表数据小于等于链化阈值，就退树成链
untreeify链化（退树成链）
这个方法是在扩容的时候，我们需要迁移红黑树的时候的处理方法
/**
* Returns a list of non-TreeNodes replacing those linked from
* this node.
* 红黑树退化成链表的方法
* 传入的map
*/
final Node<K,V> untreeify(HashMap<K,V> map) {
//hd一个链表的表头，tl一个链表的表尾
Node<K,V> hd = null, tl = null;
//这里简单来讲是循环这棵树
for (Node<K,V> q = this; q != null; q = q.next) {
//把每一棵树变成一个链表结点，这里返回一个Node类型的结点
Node<K,V> p = map.replacementNode(q, null);
//下面把链表连接起来
if (tl == null)
hd = p;
else
tl.next = p;
tl = p;
}
//返回这个链表的表头
return hd;
}红黑树代码分析
rotateLeft|Right红黑树的左旋与右旋
/* ------------------------------------------------------------ */
// Red-black tree methods, all adapted from CLR
//左旋
//参数是一个根结点，一个旋转结点
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;
//右边不等于null的时候，才有旋转的意义
if (p != null && (r = p.right) != null) {
//左有放右边（看我的红黑树旋转空口诀）
//这里先搭左边的线
if ((rl = p.right = r.left) != null)
rl.parent = p;//把父亲也搭上
//-------左边结点就搭完了---------------//
//开始搭根结点的父亲
//
if ((pp = r.parent = p.parent) == null)
//如果是根结点直接颜色变黑
(root = r).red = false;//false就代表黑
else if (pp.left == p)
//p在根结点的左边
pp.left = r;
else
//p在根结点右边
pp.right = r;
//总之最后搭p.parent这个是原则
r.left = p;
p.parent = r;
}
//最后返回这个根结点
return root;
}
//右旋和左旋是完全相反的
//里面的左变右，右变左
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}balanceInsertion红黑树的插入结点调整
//插入的调整代码
//还是一个根结点，一个插入结点
//最后返回根结点
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
x.red = true;//把结点变红，默认应该是黑色
//整体的循环判定
//xp:x的父亲结点; xpp:x的爷爷结点 xppl,xppr:x爷爷的左孩子和x爷爷的右孩子
//这里要循环递归判定
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
//如果父亲为null，那么就是根结点，直接变黑返回根结点
if ((xp = x.parent) == null) {
x.red = false;
return x;
}
//父亲为黑并且是根结点，插入为红的情况
//直接返回根结点
else if (!xp.red || (xpp = xp.parent) == null)
return root;
//这里就是左左斜的情况讨论，第三种情况插入
if (xp == (xppl = xpp.left)) {
//第三种情况里面的第四种插入情况的判断，也就是插入的结点有叔叔的情况
//这种是建立在第三种情况，左左斜上面进行分析的
//xppr叔叔不为null,并且叔叔为红色，就是第四种情况
if ((xppr = xpp.right) != null && xppr.red) {
xppr.red = false;//叔叔变黑
xp.red = false;//父亲变黑
xpp.red = true;//爷爷变红
x = xpp;//以爷爷为结点往上面进行整棵树的调整
}
//如果不是第四种情况，也就是直接是变成四结点的情况
//那就是情况三的插入
else {
//情况3还可能出现的一个情况是,不是笔直的左左斜
//也就是x在父亲的右边
if (x == xp.right) {
//拿到x的父亲左旋，这里x指向饿了
root = rotateLeft(root, x = xp);
//这一步多余其实，重新赋值了爷爷
//但是爷爷在上面的旋转过程中，又不会发生变化
xpp = (xp = x.parent) == null ? null : xp.parent;
}
//这里做了很多安全检查
//又检查了一下xp，其实这里还是没用，只要进来了这个大体的else，至少都有三个结点存在
//并且xp肯定是有父亲的
if (xp != null) {
xp.red = false;//父亲变黑
if (xpp != null) {
xpp.red = true;//爷爷变红
root = rotateRight(root, xpp);//以爷爷进行右旋
}
}
}
}//左左斜就做完了，下面就做右右的部分，与左左斜其实是完全相反的，就不过多解释了
else {
if (xppl != null && xppl.red) {
xppl.red = false;
xp.red = false;
xpp.red = true;
x = xpp;
}
else {
if (x == xp.left) {
root = rotateRight(root, x = xp);
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
xp.red = false;
if (xpp != null) {
xpp.red = true;
root = rotateLeft(root, xpp);
}
}
}
}
}
}?
?balanceDeletion红黑树删除结点调整
//删除代码调整分析
//给了一个根结点和删除结点
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
//进入循环判定
//但是删除不会往上进行整棵树的递归
//xp:父亲结点 xpl,xpr:父亲的右边和父亲的左边
for (TreeNode<K,V> xp, xpl, xpr;;) {
//x等于根结点直接返回根结点
//这种情况进来，只能说明它就只有一个根结点
//如果x等于根结点，必须保证是黑色
if (x == null || x == root)
return root;
//这里x的父亲等于null，那说明x就是根结点啊
//这里就是保证了根结点为黑色，红色为false嘛
else if ((xp = x.parent) == null) {
x.red = false;
return x;//直接返回根结点，这里确实只有这一个接点
}
//如果x是红色
else if (x.red) {
x.red = false;//直接变黑，这里其实就是对应删除情况1：自己能搞定的情况，自己能搞定，直接变黑，返回
return root;//返回根结点结束
}
//这里就要去找兄弟结点借了
//兄弟结点能借与不能借的情况
//父亲的左边是x，那么我们就是需要找右兄弟去借
else if ((xpl = xp.left) == x) {
//这里判断的是不是真正的兄弟
//如果右边不等于null，并且颜色为红色，就表示是真正的兄弟
if ((xpr = xp.right) != null && xpr.red) {
xpr.red = false;// 兄弟变黑
xp.red = true;//父亲变红
root = rotateLeft(root, xp);//利用父亲左旋
xpr = (xp = x.parent) == null ? null : xp.right;//拿到真正的兄弟
}
//下面就考虑兄弟有得借是没得借的情况
if (xpr == null)
//如果兄弟等于null,baincheng
x = xp;
else {
//有得借
//拿到兄弟的左孩子与右孩子
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
//这里是兄弟没得借的情况
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
xpr.red = true;//兄弟变红自损
x = xp;//利用父亲进行递归，父亲如果是红色，变黑，平衡
}
//下面就是兄弟有得借的情况
else {
//这里要处理的一个情况是
//找兄弟借，兄弟首先必须处理一个三结点非正常右右的情况
if (sr == null || !sr.red) {
if (sl != null)
sl.red = false;//兄弟的左边变黑
xpr.red = true;//兄弟变红//其实就是兄弟与兄弟的孩子交换颜色
root = rotateRight(root, xpr);//用兄弟右旋
xpr = (xp = x.parent) == null ?
null : xp.right;//拿到真正的兄弟
}
//下面就开始变色旋转
//之前就说了
//三结点与四节点的旋转都是共用一段代码
if (xpr != null) {
xpr.red = (xp == null) ? false : xp.red;//兄弟变成父亲的颜色
if ((sr = xpr.right) != null)
sr.red = false;//兄弟孩子变黑
}
if (xp != null) {
xp.red = false;//父亲变黑
root = rotateLeft(root, xp);//利用父亲左旋
}
x = root;//结束
}
}
}
else { // 下面操作与上面同理，右变左，左变右
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}常见的问题总结
问题1：当我们在扩容的时候，如果当前节点是红黑树的实例，他在节点迁移之后，他还会是一棵红黑树吗
答案是不一定，迁移当前桶位以及后面的节点，它是变成一棵红黑树还是单链表，取决于当前链表的迁移数目，是否大于链化阈值，如果当前链表的节点，比如低位链表的节点数目小于等于链化阈值，默认是6这个值，那么他就会把这棵树变成一个单链表存放，也就是说它会调用untreeify方法，内部会返回一个带头节点的单链表。
问题2：如果当前桶位是一个树化节点，他一定会被重新树化吗？
答案是不一定，首先这个链表会被拆分为一个高位链表和一个低位链表，如果假设这个位置，最后只有高位链表或者低位链表有数据，那么他是不会被重新树化的。
问题3：在利用红黑树putTreeVal进行数据插入的时候，相同的键是怎么处理的，是会被老值直接替换吗？
不会，在调用这个方法插入数据的时候，如果遇到相同的键，不管是能直接比较出来大小还是不能，从会直接返回原来的相同键，并不会进行替换。
?
问题4:在用红黑树的putTreeVal进行数据插入的时候，新插入的next指针的指向是指向了谁，新插入节点的父亲节点的指向又是指向了谁？
新创建的节点的next指向是指向了原来父亲的next,而父亲的next则是指向了当前这个新的节点
问题5：红黑树里面的pre节点指向的是红黑树中的父节点吗？
这里并不是，说明一下，这里是链表里面的前一个节点，这里的链表是不同的key算出来的hash值相同，然后在一个桶位形成的链表
当我们在调用putVal进行数据插入的时候，发现一个桶位达到树化条件之后，就会调用treeifyBin进行树化操作，但是这个方法内部，只会把链表的每一个节点变成一个TreeNode树节点，然后把原来的链表的next连接上，并且给原来的链表多加了一个pre指针，换句话说，就是指向了上一个节点的指针。
所以这里的pre并不是红黑树里面的父节点。
问题6：哈希表里面里面第一次形成红黑树的条件是什么？
当我们在调用putVal方法的时候，发现一个桶位中的链表数目大于了8，也就是树化的最小阈值TREEIFY_THRESHOLD，就会调用treeifyBIn进行树化操作，但是treeifyBin它不一定会去走树化这条路，它可能会调用reszie()把这个表进行扩容，扩容或者不扩容，取决于你的整个哈希表有没有最小的树化条件，也就是整个哈希表的节点必须大于MIN_TREEIFY_CAPACITY(64),才会进行树化操作。
问题7：treeify这个方法会在什么地方被调用，应用场景是什么？
首先是我们在插入的数据的时候，也就是在调用putVal的时候，当一个桶位的链表数目大于了树化阈值TREEIFY_THRESHOLD，也就是8的时候，就会调用treeifyBin这个方法，然后在treeifyBin里面还会去判断整个哈希表的结点数目大不大于一个最小的树化结点条件，也就是MIN_TREEIFY_CAPACITY(64)，大于这个数目，就要调用treeify()方法把这个桶位的链表进行树化，这是第一次的调用情况
第二次的调用情况是我们在调用resize()方法进行扩容的时候，在考虑桶位后面的结点迁移的时候，如果发现此节点是一个树结点，就要调用split()方法按照红黑树的方式对结点进行迁移，那么内部还是分为了高位链表与低位链表来处理，当结点大于链化阈值并且这个桶位高位来拿表与低位链表都有结点，就要重新树化，本身其实就是树化好了的嘛，内部也会调用treeify()方法进行重新树化
好了，先写到这，祝大家早安午安晚安。
文章来源:https://blog.csdn.net/Pxx520Tangtian/article/details/135055228
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Web--HTML基础
- Mr. Cappuccino的第68杯咖啡——基于Docker安装Oracle11g
- stelenf和sizeof的区别
- firewalld 防火墙（二）
- Hadoop分布式集群搭建
- AI编译器及TVM概述
- ***error*** (zip#Browse) unzip not available on your system
- uniapp开发小程序如何获取用户地理位置
- Flyweight享元/共享模式(对象性能)
- 一分钟带你了解人工神经网络（ANN）