数据结构----- 堆
堆的概念
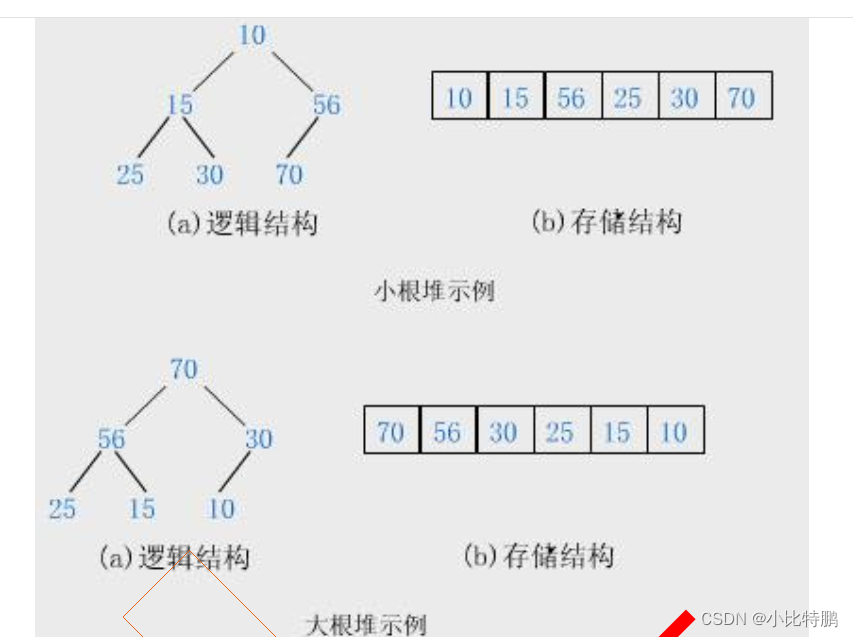
堆是在完全二叉树的基础上建立 堆又分为 大根堆和小根堆 。什么是大根堆呢?就是说里面的任意结点的值都满足大于其子树中结点的值这个条件 则说明该堆是大根堆(最大堆)与其相反就称为小根堆(最小堆)。
堆的性质
1、堆中某个节点的值总是不大于或者不小于其父节点的。
2、堆总是一棵完全二叉树。
下面我们通过图例来区分 大根堆和小根堆
堆的存储方式
我们从堆的概念可以得知:堆是一棵完全二叉树 所以我们可以通过层序遍历的方式进行存储 从而达到空间的充分利用 实现高效性。但是这种存储方式仅适用于完全二叉树 因为非完全二叉树会存在空间的浪费。为了还原二叉树 必然会使空间的利用率下降。下面我们通过图例就可以清晰的了解。
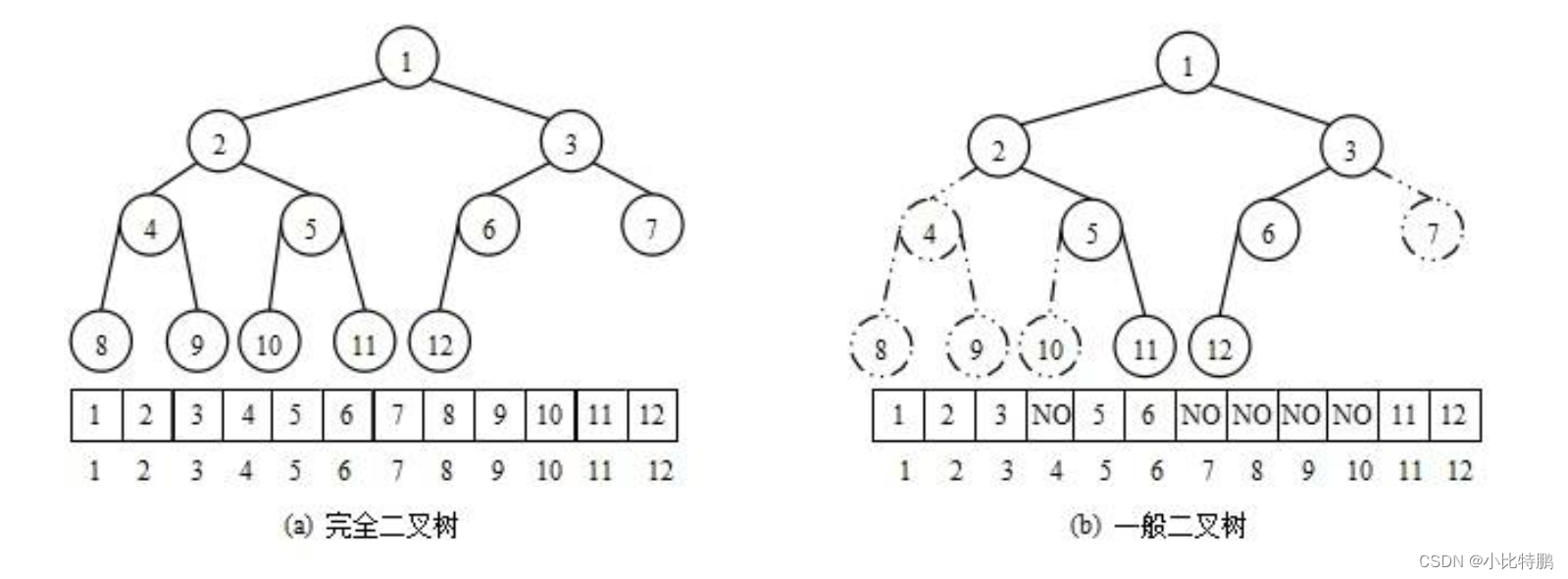
可以看到一般的二叉树存在很多不能省略的空节点 会导致存储成完整的二叉树的空间利用率降低。
顺序存储中父节点和孩子节点的下标关系
现在假设i为节点在数组中的下标,则:
1、如果i为0,则表示的节点为根节点,否则节点的双亲节点为(i/1)/2
2、如果2 * i + 1小于节点的个数,则节点i的左孩子下标为2 * i +1,否则没有左孩子
3、如果2 * i + 2小于节点的个数,则说明节点的右孩子下标为2 * i +2,否则没有右孩子
建堆
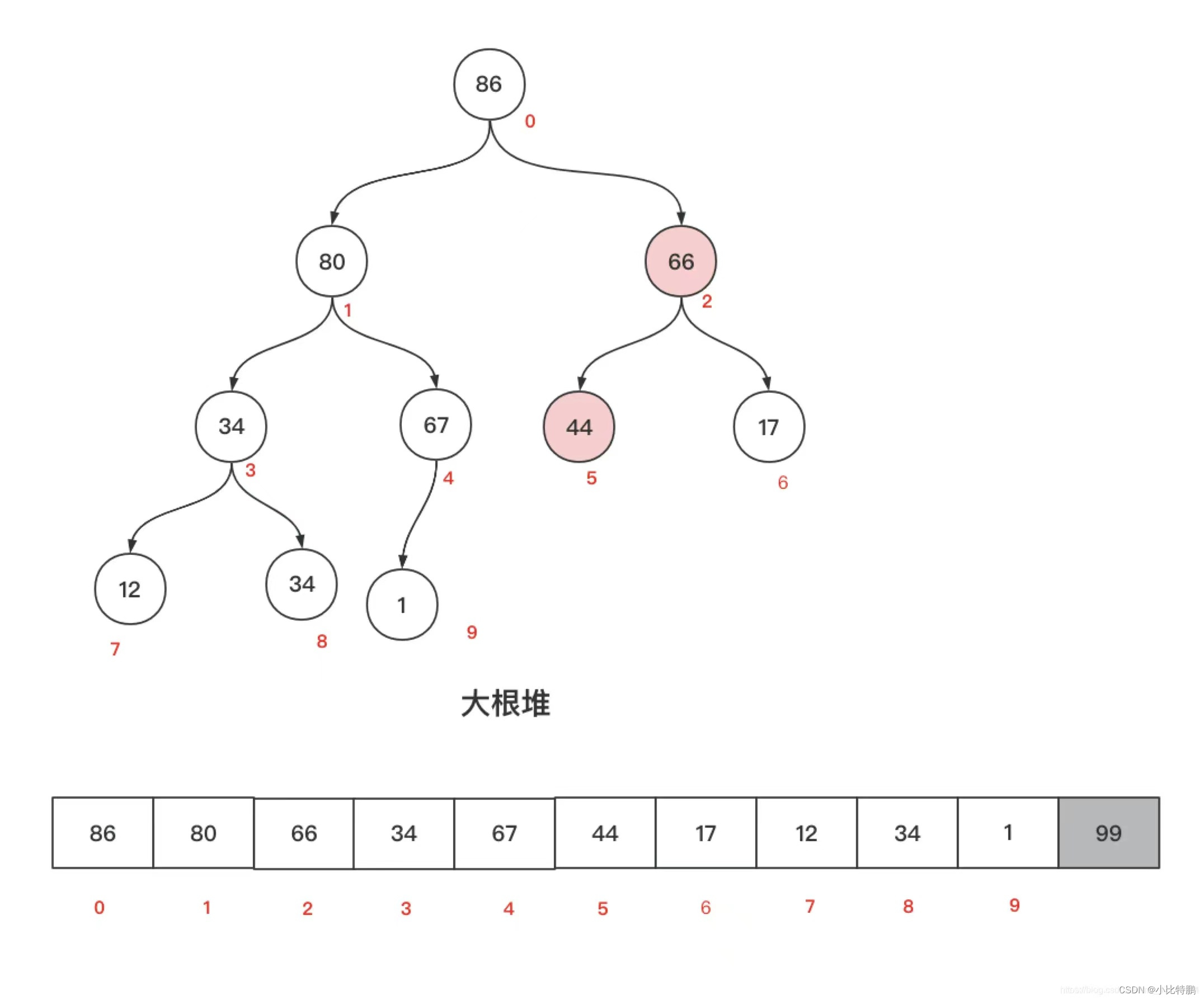
我们以大根堆为例,向上调整建堆。
public class TextHeap {
public int[] elem;
public int usedSize;
public TextHeap(){
this.elem = new int[10];
}
public void initElem(int[] array){
for (int i = 0; i < array.length; i++){
elem[i] = array[i];
usedSize++;
}
}
//创建一个大根堆
public void createBigHeap(){
for (int parent = (usedSize -1 -1)/2; parent >= 0; parent--) {
siftDown(parent,usedSize); //大根堆
//siftDown2(parent,usedSize); //小根堆
}
}
// 创建大根堆
private void siftDown(int parent, int end){
int child = 2 * parent + 1;
while (child < end){
//确定左右结点哪个是最大的
if (child + 1 < usedSize && elem[child] < elem[child+1]){
child++;
}
//走到这里 child一定是左右孩子最大值的下标
if (elem[child] > elem[parent]){
//就要交换
swap(child,parent);
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}
以上就是通过向上调整的方式建大根堆的实现代码(小根堆其实和大根堆的创建差不多 就一些判断条件改一下)
时间复杂度
根据代码难以看出它的时间复杂度 要通过计算才能得到它的时间复杂度
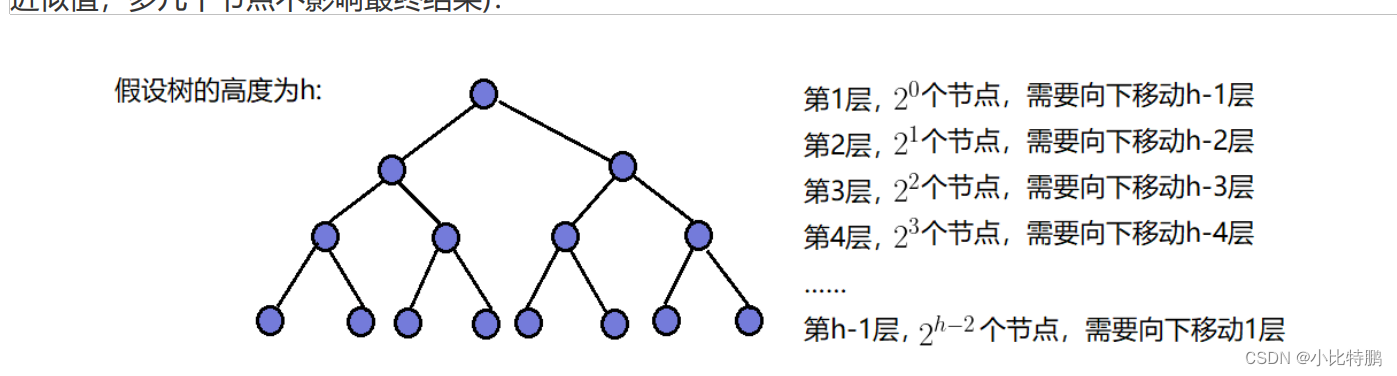
涉及到每一层有多少个节点,时间复杂度与节点的高度h和每一层节点的个数有关。

通过上面图片的演算过程可以得到T(n) = n-log2(n+1);你们知道最后为什么时间复杂度是O(n)吗? 因为根据数学的极限思想 随着n越来越大。整个表达式的结果就越趋近于n。
堆的应用
优先级队列:应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。优先级队列实现的方法最常用的就是使用堆来构建。
堆的删除
堆的删除一定是删除堆顶元素。 具体实现方式如下:
1、将堆顶元素和堆中最后一个元素交换
2、将堆的有效元素减少一个
3、对堆顶元素进行调整
具体代码如下:
//删除元素
public int poll() {
int tmp = elem[0];
swap(0,usedSize-1);
usedSize--;
siftDown(0,usedSize);
return tmp;
}
对了还要判空 代码没写 就写一个**isEmpty()**补上就行。
堆的插入
堆的插入需要分两步走:
1、先将元素放入到底层空间中(空间不够就得扩容)
2、将最后新插入的元素再进行调整成满足堆的性质
代码实现如下:
//大根堆的插入
public void offer(int val){
if (isFull()){
isCopyof();
}
this.elem[this.usedSize++]=val;
shiftUp(this.usedSize-1);
}
//是否为满
public boolean isFull(){
return this.usedSize == this.elem.length;
}
public void isCopyof(){
this.elem = Arrays.copyOf(this.elem,this.elem.length*2);
}
获取堆顶元素(peek)
这个就很容易了 直接返回下标为0的数值。
代码实现如下:
public int peekHeap(){
return elem[0];
}
堆的Top-K问题
现在有个问题:假如给你100万个游戏账号 ,取出前面8个等级最高的账号。
思路:
1、我们肯定要把堆调整成大根堆
2、我们把前K个数据拿出来建堆 ,建立一个大小为K的大根堆,把k下标后面的数据都和堆顶的元素一一比较,如果比他小就插入堆 以此类推下去。
上面是找前K个最小的元素,如果想找前K个最大元素,则相反建堆则为小堆。
代码实现如下:
public int[] smallestK(int[] arr,int k){
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new Imp());
for (int i = 0;i < k;i++){
maxHeap.offer(arr[i]);
}
//比较k下标之后的元素与堆顶元素的大小
for (int i = k;i < arr.length;i++){
int top = maxHeap.peek();
if (arr[i] < top) {
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
int[] tmp = new int[k];
for (int i = 0;i < k;i++){
tmp[i] = maxHeap.poll();
}
return tmp;
}
//重新写一个比较器
class Imp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
}
堆排序
利用堆这种数据结构来进行排序,有两个步骤:
1.建堆
如果是升序:建大根堆
反之则是建小跟堆
2、利用堆删除的思想来进行排序
下面我们以升序来用代码来实现一下堆排序:
//堆排序 从小到大 用大根堆
public void heapSort() {
int end = usedSize - 1;
while (end > 0){
swap(0,end);
siftDown(0,end-1);
end--;
}
}
力扣中的一道堆的Top-K问题 大家可以试试
最小K问题
好了以上就是我们的全部内容 所有代码实现看下面:
import java.util.Arrays;
public class TextHeap {
public int[] elem;
public int usedSize;
public TextHeap(){
this.elem = new int[10];
}
public void initElem(int[] array){
for (int i = 0; i < array.length; i++){
elem[i] = array[i];
usedSize++;
}
}
//创建一个大根堆
public void createBigHeap(){
for (int parent = (usedSize -1 -1)/2; parent >= 0; parent--) {
siftDown(parent,usedSize); //大根堆
//siftDown2(parent,usedSize); //小根堆
}
}
// 创建大根堆
private void siftDown(int parent, int end){
int child = 2 * parent + 1;
while (child < end){
//确定左右结点哪个是最大的
if (child + 1 < usedSize && elem[child] < elem[child+1]){
child++;
}
//走到这里 child一定是左右孩子最大值的下标
if (elem[child] > elem[parent]){
//就要交换
swap(child,parent);
parent = child;
child = 2*parent+1;
}else {
break;
}
}
}
//小根堆的建立
private void siftDown2(int parent, int end){
int child2 = 2 * parent + 1;
while (child2 < end){
//确定左右子树哪个最小
if (child2 + 1 < usedSize && elem[child2] > elem[child2+1]){
child2++;
}
//走到这里 child就是左右孩子最小值的下标
if (elem[child2] < elem[parent]){
//交换
swap(child2,parent);
parent = child2;
child2 = 2*parent + 1;
}else {
break;
}
}
}
private void swap(int i, int j){
int tmp = elem[i];
elem[i] = elem[j];
elem[j] = tmp;
}
//删除元素
public int poll() {
int tmp = elem[0];
swap(0,usedSize-1);
usedSize--;
siftDown(0,usedSize);
return tmp;
}
//向上调整法
public void shiftUp(int child){
int parent = (child-1)/2;
while (parent >= 0){
if (elem[parent] <elem[child]){
swap(parent,child);
child = parent;
parent = (child-1)/2;
}else {
break;
}
}
}
//大根堆的插入
public void offer(int val){
if (isFull()){
isCopyof();
}
this.elem[this.usedSize++]=val;
shiftUp(this.usedSize-1);
}
//是否为满
public boolean isFull(){
return this.usedSize == this.elem.length;
}
public void isCopyof(){
this.elem = Arrays.copyOf(this.elem,this.elem.length*2);
}
public int peekHeap(){
return elem[0];
}
//堆排序 从小到大 用大根堆
public void heapSort() {
int end = usedSize - 1;
while (end > 0){
swap(0,end);
siftDown(0,end-1);
end--;
}
}
//重新写一个比较器
class Imp implements Comparator<Integer> {
@Override
public int compare(Integer o1, Integer o2) {
return o2.compareTo(o1);
}
}
public class Text2 {
//第二种求最小K问题的方法 用最大根解决 只需要把前K个元素出来建堆 剩下的就和堆顶进行比较比较就行 如果比堆顶元素小 就把该元素offer进堆
public int[] smallestK(int[] arr,int k){
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(new Imp());
for (int i = 0;i < k;i++){
maxHeap.offer(arr[i]);
}
//比较k下标之后的元素与堆顶元素的大小
for (int i = k;i < arr.length;i++){
int top = maxHeap.peek();
if (arr[i] < top) {
maxHeap.poll();
maxHeap.offer(arr[i]);
}
}
int[] tmp = new int[k];
for (int i = 0;i < k;i++){
tmp[i] = maxHeap.poll();
}
return tmp;
}
//最小K问题 用最小根解决 先把堆调整为小根堆 再输出前k个多值
public int[] smallestK1(int[] arr, int k){
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
for (int i = 0;i<arr.length;i++){
minHeap.offer(arr[i]);
}
int[] tmp = new int[k];
for (int i = 0;i < k;i++){
tmp[i] = minHeap.poll();
}
return tmp;
}
}
最后感谢大家的观看 谢谢大家 !!!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!