动态规划day03

343. 整数拆分(第二次做还是没弄明白)

力扣题目链接(opens new window)

给定一个正整数?n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。

示例 1:

• 输入: 2
• 输出: 1
• 解释: 2 = 1 + 1, 1 × 1 = 1。

示例?2:

• 输入: 10
• 输出: 36
• 解释: 10 = 3 + 3 + 4, 3 ×?3 ×?4 = 36。

看到题目的第一想法

? ? ? ? dp ，列出最大乘积找规律，发现，按照3来拆分是能达到最大乘积的

? ? ? ? dp[i] 代表最大的乘积

? ? ? ? 根据规律进行初始化，将dp[i-3] 与3 相乘

? ? ? ? 但我的做法不太符合dp的规律

看到代码随想录之后的想法

? ? ? ? 拆分成近似的数时，得到的乘积是最大的

? ? ? ? 动规五部曲，很快的写出解题思路

? ? ? ? 1确定dp数组以及对应下标的含义

????????dp[i] 代表最大的乘积

? ? ? ? 2确定递推公式

? ? ? ? dp[i][j] = dp[i-1][j]+dp[i][j-1]

????????3dp数组初始化

? ? ? ? 需要把第一行和第一列都初始化，都为1

? ? ? ? 4确定遍历顺序

? ? ? ? 从上往下，从前往后

? ? ? ? 5手动推导dp数组

? ? ? ? 6打印dp数组

? ? ? ? 打印dp[m-1][n-1]

自己实现过程中遇到的困难

? ? ? ? 注意初始化

class Solution {
    /*public int integerBreak(int n) {
        //确定dp和每个下标的含义
        //dp的每个下标对应每一个数的最大乘积？
        //确定递推公式
        //5开始，然后3加上对应下标的最大乘积
        //确定dp数组的初始条件
        //dp[0]=1 dp[1]=1 dp[2]=2 
        //确定遍历顺序
        //从前往后
        //举例推导dp数组
        //dp[0]=1 dp[1]=1 dp[2]=2 dp[3]=2 dp[4] =4 dp[5]=6 dp[6]=9 dp[7] = 3*dp[7-3] dp[8]=3+dp[8-3] 
        //打印dp数组
        if(n==2){
            return 1;
        }
        if(n==3){
            return 2;
        }
        if(n==4){
            return 4;
        }
        if(n==5){
            return 6;
        }
        if(n==6){
            return 9;
        }
        int dp[] = new int[n];
        dp[1]=1;dp[2]=2;dp[3]=4;dp[4]=6;dp[5]=9;
        for(int i=6;i<n;i++){
            dp[i]=3*dp[i-3];
        }
        return dp[n-1];
    }*/
    //卡哥做法
    //我的做法的问题，dp的初始值设置的过多，违背的dp的本来含义，有点类似于拆成很多个3的感觉
    //卡哥做法:拆分当前值，存到dp数组中，dp[i] = max(i*(i-j),i*dp[i-j],dp[i]);
    // j*(i-j) 就是当前数拆成两个
    // j*dp[i-j] 就是当前数，和之前dp得到的最大数相乘的最大值，dp[i-j]存放的是拆分i-j所得到的最大值
    // dp[i] 记录就是得到的值动态变化，变化中的最大值就是dp[i] 
     public int integerBreak(int n) {
        //确定dp和每个下标的含义
        //dp的每个下标对应每一个数的最大乘积？
        //确定递推公式
        //dp[i] = max(dp[i],j*(i-j),dp[i-j]*j)
        //确定dp数组的初始条件
        //dp[0]=0 dp[1]=0 dp[2]=1 
        //确定遍历顺序
        //从前往后
        //举例推导dp数组
        //dp[0]=0 dp[1]=0 dp[2] = 1
        //打印dp数组
        if(n==0){
            return 0;
        }
        if(n==1){
            return 0;
        }
        if(n==2){
            return 1;
        }
        int dp[] = new int[n+1];
        dp[0]=0;
        dp[1]=0;
        dp[2]=1;
        //注意是每个下标对应目标的值
        for(int i=3;i<=n;i++){
            //因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。
            //m一定>=2所以只要拆到i/2就行了 ，再往后拆一定不是最大值 
            for(int j=1;j<=i/2;j++){
                dp[i] = Math.max(dp[i],Math.max(j*(i-j),dp[i-j]*j));
            }
        }
        return dp[n];
    }
}

96. 不同的二叉搜索树

(总结时还是不太会)

给你一个整数?n?，求恰由?n?个节点组成且节点值从?1?到?n?互不相同的?二叉搜索树?有多少种？返回满足题意的二叉搜索树的种数。

示例 1：

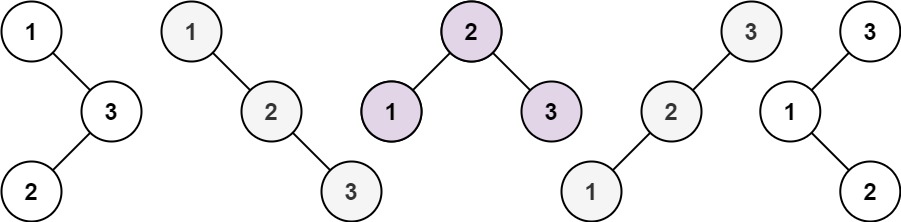
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

看到题目的第一想法

? ? ? ? dp ，记录种数

? ? ? ? 但是没找到规律

看到代码随想录之后的想法

? ? ? ? 动规五部曲，很快的写出解题思路

? ? ? ? 1确定dp数组以及对应下标的含义

????????dp[i] 代表不同的种数

? ? ? ? 2确定递推公式

? ? ? ? 左子树为0 右子树为n-1 dp[0]*dp[n-1]

? ? ? ? 左子树为1 右子树为n-2? dp[1]*dp[n-2]

? ? ? ? ?左子树为2 右子树为n-3? dp[2]*dp[n-3]

? ? ? ? ?左子树为3 右子树为n-4? ?dp[3]*dp[n-4]

? ? ? ? 。。。

? ? ? ? 左子树为n-1 右子树为0 dp[n-1]*dp[0]

? ? ? ? 第n棵树的种数就是把上述的都加起来

? ? ? ? dp[n]=dp[n-1]*dp[0]+dp[n-2]*dp[1]

? ? ? ? for循环0~i 累加起来

????????
? ? ? ? ? ? ? ? //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
? ? ? ? ? ? ? ? //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
? ? ? ? ? ? ? ? dp[i]+=dp[j-1]*dp[i-j];

????????3dp数组初始化

? ? ? ? dp[0]=1

? ? ? ? 4确定遍历顺序

? ? ? ? 从前往后

? ? ? ? 5手动推导dp数组

? ? ? ? 6打印dp数组

? ? ? ? 打印dp[m-1][n-1]

自己实现过程中遇到的困难

? ? ? ? 注意初始化

? ? ? ? 注意是双重for循环 外层0~n 里层0~i

? ? ? ? 将根节点编号比较好理解? 当根节点为第j个节点时，左边为j-1 右边为 i-jdp[j-1]*dp[i-j]

class Solution {
    //我没想到思路，卡哥给的思路是和正数拆分差不多，也是分为i j 来拆
    //第i棵二叉树的种数为 
    // 左边为i-1*右边为0 dp[i-1]*dp[0]
    // 左边为i-2*右边为1 dp[i-2]*dp[1]
    // 左边为i-3*右边为2 dp[i-3]*dp[2]
    // ... 把以上的相加
    public int numTrees(int n) {
        //确定dp数组以及每个下标的含义
        //当前二叉搜索树的种数
        //确定递推公式
        //dp[i]=dp[i-1]*dp[0]+dp[i-2]*dp[1]+dp[i-3]*dp[2]...
        //dp[i] = for(从j=0开始到i-1dp所记录的相乘)
        //dp数组的初始化
        //空树为0
        //dp[0]=1 dp[1]=1
        //确定遍历顺序
        //从前往后
        //举例推导dp数组
        //dp[0]=0 dp[1] = dp[0]*dp[0] =1 dp[2] = dp[1]*dp[0]+dp[0]*dp[1]=2
        int[] dp = new int[n+1];
        dp[0]=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                //如果dp[1]=dp[0]*dp[0]
                //这里是dp[j-1]*dp[i-j]
                // 举例 若i为4
                // 0 3 j=1
                // 1 2 j=2
                // 2 1 j=3
                // 3 0 j=4
                //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
                //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
                dp[i]+=dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
}