机器学习---特征选择与稀疏学习

1. 特征

特征：描述物体的属性。

特征的分类：相关特征: 对当前学习任务有用的属性；无关特征: 与当前学习任务无关的属性

?特征选择：从给定的特征集合中选出任务相关特征子集；必须确保不丢失重要特征。?

原因：减轻维度灾难：在少量属性上构建模型；降低学习难度：留下关键信息

特征选择的一般方法：遍历所有可能的子集；计算上遭遇组合爆炸，不可行。

可行方法：

两个关键环节：子集搜索和子集评价。若要从初始的特征集合中选取一个包含了所有重要信息的特

征子集，如果没有任何领域知识作为先验假设，那就只好遍历所有可能的子集了。然而，这在计算

上是不可行的，因为这样做会遭遇组合爆炸，特征个数稍多，就无法进行。

1.1 子集搜索

用贪心策略选择包含重要信息的特征子集；前向搜索：最优子集初始为空集，逐渐增加相关特征

后向搜索：从完整的特征集合开始，逐渐减少特征；双向搜索：每一轮逐渐增加相关特征，同时减

少无关特征。特征选择的第一个环节，是“子集搜索”问题，通常我们选择用贪心策略选择包含重要

信息的特征子集。即，仅考虑了本轮选定的特征集合是最优的。

1.2 子集评价

特征子集A 确定了对数据集D的一个划分：每个划分区域对应着特征子集A的某种取值。样本标记Y

对应着对数据集的真实划分。通过估算这两个划分的差异，就能对特征子集进行评价；与样本标记

对应的划分的差异越小，则说明当前特征子集越好。信息熵是判断这种差异的一种方式：

特征选择的第二个环节，是“子集评价”问题，对于特征子集 A 确定了对 数据集?D 的一个划分，每

个划分区域对应着特征子集 A 的某种取值，样本标记信息 Y 对应着对数据集 D 的真实划分。通过

估算这两个划分的差异，就能对特征子集 A 进行评价；与 样本标记 Y 对应的划分的差异越小，则

说明当前特征子集 A 越好。我们可以选择信息熵来判断这种差异。

2.?常见的特征选择方法

将特征子集搜索机制与子集评价机制相结合，即可得到特征选择方法。

2.1 过滤式

先对数据集进行特征选择，然后再训练学习器，特征选择过程与后续学习器无关。先用特征选择过

程过滤原始数据，再用过滤后的特征来训练模型。

Relief (Relevant Features) 方法是一种著名的过滤式特征选择方法。Relief算法最早由Kira提出，

最初局限于两类数据的分类问题。Relief算法是一种特征权重算法(Feature?weighting?algorithms)，

根据各个特征和类别的相关性赋予特征不同的权重（相关统计量），权重小于某个阈值的特征将被

移除。Relief算法中特征和类别的相关性是基于特征对近距离样本的区分能力。Relief的关键是如何

确定权重（相关统计量）？

Relief算法从训练集D中随机选择一个样本?𝒙𝑖?，然后从和?𝒙𝑖?同类的样本中寻找最近邻样本，称为

猜中近邻（near-hit）；从和?𝒙𝑖?不同类的样本中寻找最近邻样本，称为猜错近邻（near-miss），

然后根据以下规则更新每个特征的权重：如果?𝒙𝑖?和猜中近邻在某个特征上的距离小于?𝒙𝑖?和猜错近

邻上的距离，则说明该特征对区分同类和不同类的最近邻是有益的，则增加该特征的权重；反之，

如果?𝒙𝑖?和猜中近邻在某个特征的距离大于?𝒙𝑖?和猜错近邻上的距离，说明该特征对区分同类和不同

类的最近邻起负面作用，则降低该特征的权重。以上过程重复m次，最后得到各特征的平均权重。

特征的权重越大，表示该特征的分类能力越强，反之，表示该特征分类能力越弱。Relief方法的时

间开销随采样次数以及原始特征数线性增长，运行效率很高。

Relief算法比较简单，但运行效率高，并且结果也比较令人满意，因此得到广泛应用，但是其局限

性在于只能处理两类别数据。1994年Kononeill进行了扩展，得到了ReliefF作算法，可以处理多类

别问题，用于处理目标属性为连续值的回归问题。ReliefF算法在处理多类问题时，每次从训练样

本集中随机取出一个样本𝒙𝑖?，从和?𝒙𝑖?同类的样本集中找出?𝒙𝑖?的1个猜中近邻样本，从每个?𝒙𝑖?的不

同类的样本集中均找出k-1个猜错近邻样本。然后，更新每个特征的权重。

医学数据分析实例：

选用的数据：威斯康星州乳腺癌数据集，数据来源美国威斯康星大学医院的临床病例报告，每条数

据具有9个属性。

数据处理思路：先采用ReliefF特征提取算法计算各个属性的权重，剔除相关性最小的属性，然后

采用K-means聚类算法对剩下的属性进行聚类分析。?

乳腺癌数据集特征提取：采用ReliefF算法来计算各个特征的权重，权重小于某个阈值的特征将被

移除，针对乳腺癌的实际情况，将对权重最小的2-3种剔除。将ReliefF算法运行20次，得到了各个

特征属性的权重趋势图。

按照从小到大顺序排列，可知，各个属性的权重关系如下：属性9<属性5<属性7<属性4<属性2<属

性3<属性8<属性1<属性6。我们选定权重阀值为0.02，则属性9、属性4和属性5剔除。

从上面的特征权重可以看出，属性6裸核大小是最主要的影响因素，说明乳腺癌患者的症状最先表

现了裸核大小上，将直接导致裸核大小的变化，其次是属性1和属性8等，后几个属性权重大小接

近。几个重要的属性进行分析：

块厚度属性的特征权重在0.19-25左右变动，也是权重极高的一个，说明该特征属性在乳腺癌患者

检测指标中是相当重要的一个判断依据。进一步分析显示，在单独对属性6，和属性1进行聚类分

析，其成功率就可以达到91.8%。

2.2 包裹式

直接把最终将要使用的学习器的性能作为特征子集的评价准则。

包裹式特征选择的目的就是为给定学习器选择最有利于其性能、“量身定做”的特征子集。包裹式选

择方法直接针对给定学习器进行优化，因此从最终学习器性能来看，包裹式特征选择比过滤式特征

选择更好，包裹式特征选择过程中需多次训练学习器，计算开销通常比过滤式特征选择大得多，

LVW（Las Vegas Wrapper）是一个典型的包裹式特征选择方法， LVW在拉斯维加斯方法框架下

使用随机策略来进行子集搜索，并以最终分类器的误差作为特征子集评价准则。

LVW基本步骤：在循环的每一轮随机产生一个特征子集；在随机产生的特征子集上通过交叉验证推

断当前特征子集的误差；进行多次循环，在多个随机产生的特征子集中选择误差最小的特征子集作

为最终解。采用随机策略搜索特征子集，而每次特征子集的评价都需要训练学习器，开销很大。

2.3 嵌入式

将特征选择过程与学习器训练过程融为一体，两者在同一个优化过程中完成，在学习器训练过程中

自动地进行特征选择。

考虑最简单的线性回归模型，以平方误差为损失函数，并引入L2范数正则化项防止过拟合，则有

将L2范数替换为L1范数，则有LASSO [Tibshirani, 1996]：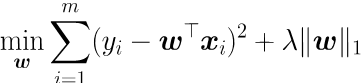

L2范数和L1范数均有助于降低过拟合风险，但是L1范数易获得稀疏解，即w会有更少的非零分量，

是一种嵌入式特征选择方法，L1正则化问题的求解可使用近端梯度下降算法。

3. 稀疏表示

将数据集D考虑成一个矩阵，每行对应一个样本，每列对应一个特征。特征选择说考虑的问题是特

征具有稀疏性，即矩阵中的许多列与当前学习任务无关，通过特征选择去除这些列，则学习器训练

过程仅需在较小的矩阵上进行，学习任务的难度可能有所降低，设计的计算和存储开销会减少，学

得模型的可解释性也会提高。矩阵中有很多零元素，且非整行整列出现。

稀疏表达的优势：数据具有稀疏性，使得大多数问题变得线性可分；稀疏矩阵已有很多高效的存储

方法。

图1.1 给出了Candes 等人在对核磁共振成像(Magnetic Resonance Imaging，MRI)进行研究时得到

的实验结果。其中图1.1(a)为原始图像，图1.1(b)中的一条直线表示在傅里叶变换域中的一次测

量。由于?MRI 中测量数据不再直接对应于图像各个像素的灰度值，而是图像经过全局傅里叶变换

(Fourier Transform)后的数据。因此为了获得清晰的图像，传统方法需要对图像进行大量的测量，

即密集的线。当只使用如图1.1(b)所示的18 条线进行测量时，由于测量得到的数据只占整个频域的

7.71%，因此由传统的后向投影方法(Back Projection，BP)重建得到的图像如图1.1(c)所示，重建

图像的质量很差。但是如果在重构模型中加入稀疏性约束后获得的重建图像则如图1.1(d)所示，可

以看到得到的重建图像与原始图像相比并没有明显差别。

3.1 字典学习

在一般的学习任务中，数据集（如图像）往往是非稀疏的，能否将稠密表示的数据集转化为“稀疏

表示”，使其享受稀疏表达的优势？为普通稠密表达的样本找到合适的字典。

在一般的学习任务中，数据集（如图像）往往是非稀疏的，能否将稠密表示的数据集转化为“稀疏

表示”，使其享受稀疏表达的优势？为普通稠密表达的样本找到合适的字典，将样本转化为稀疏表

示，这一过程称为字典学习。给定数据集X，字典学习目标是字典矩阵D以及样本的稀疏向量𝛼?，

字典学习的优化形式为，采用变量交替优化策略求解字典D和稀

疏向量𝛼𝑖?固定字典D，为每个样本𝒙𝑖?找到对应的𝛼𝑖? ：

以𝛼𝑖?为初值，更新字典D：

字典学习的常用解法：K-SVD，核心思想：K-SVD最大的不同在字典更新这一步，K-SVD对误差

矩阵𝐄𝑖?进行奇异值分解，取得最大奇异值对应的正交向量更新字典中的一个原子，同时并更新其

对应的稀疏系数，直到所有的原子更新完毕，重复迭代几次即可得到优化的字典和稀疏系数。

3.2?压缩感知

压缩感知是由美国学者E. Candes和T. Tao于2004年首先提出的。“压缩感知”顾名思义是直接感知

压缩后的信息，其目的是从尽量少的数据中提取尽量多的信息。CS 理论证明了如果信号在正交空

间具有稀疏性（即可压缩性），就能以远低于Nyquist采样频率的速率采样该信号，最后通过优化

算法高概率重建出原信号。其基本思想是一种基于稀疏表示的信号压缩和重构技术，也可以称为压

缩采样或稀疏采样。

从图1.2 可以看出，在基于Nyquist 采样的传统信息获取系统中，采样端通过探测器得到采样数据

后，在对数据进行存储和传输之前，首先采用压缩技术对数据进行压缩，尽可能多地减少数据量；

然后在接收端通过相应的解压缩技术，就能够有效地还原出原始信号。虽然压缩理论[29-38]能够有

效缓解海量数据带来的数据处理、存储和传输压力，但是仍然无法解决由采样端造成的资源浪费问

题，因为在压缩过程中大量不重要的冗余数据被抛弃掉了。

而在CS 信息获取系统中(如图1.3 所示)，数据的采样与压缩同步以低速率进行，只对那些包含了信

号重要信息的数据进行采样，从而节约了大量的采样资源，有望从根本上解决传统信息获取系统

中，为了获取高分辨率图像而盲目追求高分辨率探测器而带来的高成本问题。

压缩感知是由美国学者E. Candes和T. Tao于2004年首先提出的。“压缩感知”顾名思义是直接感知

压缩后的信息，其目的是从尽量少的数据中提取尽量多的信息。CS 理论证明了如果信号在正交空

间具有稀疏性（即可压缩性），就能以远低于Nyquist采样频率的速率采样该信号，最后通过优化

算法高概率重建出原信号。其基本思想是一种基于稀疏表示的信号压缩和重构技术，也可以称为压

缩采样或稀疏采样。

压缩感知引起了信号采样及相应重构方式的本质性变化，即：数据的采样和压缩是以低速率同步进

行的，这对于降低信息获取系统的采样成本和资源都具有重要意义。

由于压缩感知技术突破了传统香农采样定理的限制，其理论研究已经成为应用数学、数字信号处

理、数字图像处理等领域的最热门的方向之一，同时其应用领域涉及到图像压缩、医学图像处理、

生物信息处理、高光谱影像、地球物理数据分析、压缩雷达、遥感和计算机图像处理等诸多方面。

长度为MM的离散信号𝒙，用远小于奈奎斯特采样定理的要求的采样率采样得到长度为NN的采样后

信号𝒚。一般情况下，N?MN?M，不能利用𝒚?还原𝒙，但是若存在某个线性变换Ψ，使得𝒙=Ψ𝜶?，

即可以近乎完美地恢复𝒙。

压缩感知关注的问题是如何利用信号本身具有的稀疏性，从部分观测样本𝒚?中恢复原始信号𝒙。

压缩感知需要解决的三个问题：感知测量（信号的稀疏表示），设计观测矩阵Ф，信号重构技术。

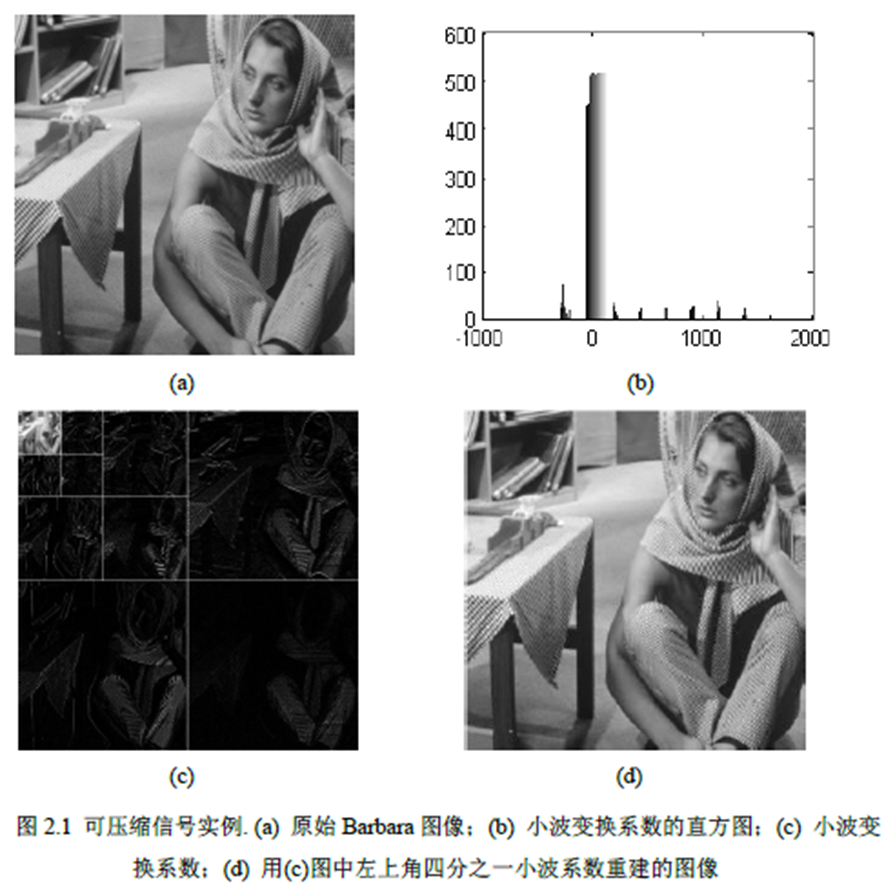
图2.1 给出了一个可压缩信号的实例，从图2.1(b)中可以看出Barbara 图像通过Haar 小波变换后，

除少量的系数外大部分系数的幅值接近于零。图2.1(d)中利用了占所有系数中四分之一的大系数，

就重构得到具有较高质量的目标图像。?

3.3?压缩感知的核心问题

感知测量：信号的最佳稀疏域表示是压缩感知理论应用的基础和前提，只有选择合适的基ΨΨ表示

信号才能保证信号的稀疏度，从而保证信号的恢复精度。涉及到前面介绍的稀疏编码和字典学习。

设计观测矩阵Φ：观测矩阵Ф是压缩感知理论采样的实现部分。通过观测矩阵控制的采样使得目标

信号𝒙?在采样过程中即被压缩，同时保证目标信号所含有效信息不丢失，能够由压缩采样值还原出

目标信号。如何设计一个平稳的、与变换基不相关、满足有限等距（RIP，即从观测矩阵中抽取的

每M个列向量构成的矩阵是非奇异的）性质的观测矩阵Ф，同时保证稀疏向量从N维降维到M维时

重要信息不遭破坏（即信号低速采样问题），是压缩感知的另一个重要研究内容。目前常用的测量

矩阵主要有：高斯随机矩阵、伯努利随机矩阵(又称二值随机矩阵) 、局部哈达玛矩阵、局部傅里叶

矩阵、Chirp 序列、Altop 序列、托普利兹矩阵等。

信息重构技术：重构算法是从采样值求解最优化问题寻找到目标信号最优解。在压缩感知理论中,

由于观测值M远小于信号𝒙?的长度N，因此，信号重构的核心在于如何求解欠定方程组𝒚=ФΨ𝒙。如

果信号 是稀疏的或可压缩的，且观测矩阵Ф?具有有限等距RIP性质，那么从M个观测值中精确恢复

信号𝒙?是可能的。

信号重构的常用方法：

𝑙0?范数非凸优化问题：贪婪算法，如匹配追踪、正交匹配追踪算法等。

𝑙1?范数凸优化问题：线性规划方法进行求解，如基追踪、梯度投影稀疏重构算法、 迭代分裂阈值

算法等。

𝑙𝑝?范数非凸优化问题：通过p范数优化问题求解来找到信号的“最优”逼近。

Bayesian 方法：其思想是首先合理假设未知的信号系数具有某种稀疏性的先验概率分布，然后根

据压缩观测信号对未知系数的后验概率分布进行推理。该类方法还能够估计出重构问题的解的误差

范围，这一优点是传统优化方法所不具备的。