国科大图像处理2023速通期末——汇总2017-2019
国科大2023.12.28图像处理0854期末重点
图像处理 王伟强 作业 课件 资料
一、填空
- 一个阴极射线管它的输入与输出满足 s = r 2 s=r^{2} s=r2,这将使得显示系统产生比希望的效果更暗的图像,此时伽马校正通常在信号进入显示器前被进行预处理,令p与q表示伽马校正的输入与输出,则p与q之间的映射关系式表示为: q = p 1 2 q=p^{\frac{1}{2}} q=p21?
- 卷积是一种图像处理领域最有影响力的计算之一,对于一幅输入图像f(x,y), 我们可以通过卷积运算产生一幅新的图像g(x,y),若g(x,y)=0.1f(x+1,y)+0.2f(x-1y)+0.3f(x,y)+0.2f(x,y-1)+0.2f(x,y+1)这里x表示行标,y表示图像中像素位置的列坐标,请用一个3X3的矩阵来表示这个卷积核
- 我们处理一幅图像可以在空域中通过线性滤波运算进行处理,也可以在频域内对它进行处理达到同样的效果。该事实的理论基础就是基于傅立叶变换的卷积定理,若我们用f(x,y),g(x,y)表示图像与线性滤波核,它们对应的傅立叶变换分别用F(u,v),G(u,v)表示则该定理可形式化描述为f(x,y)?g(x,y)?F(u,v)×G(u,v)
- 拉普拉斯波器的频域表示的函数形式为 H ( u , v ) = ? 4 π 2 ( u 2 + v 2 ) H(u,v)=-4\pi ^{2}(u^{2}+v^{2}) H(u,v)=?4π2(u2+v2)
- 假设我们有一个在0-1区间的均匀分布随机数发生器w,若已知一个满足瑞利分布的随机变量累加分布函数CDF是 F z ( z ) = { 1 ? e x p ( ? ( z ? a ) 2 b ) , z ≥ a 0 , z < a F_{z}(z)=\begin{cases} 1-\frac{exp(-(z-a)^{2}}{b}),z\ge a\\ 0,z<a \end{cases} Fz?(z)={1?bexp(?(z?a)2?),z≥a0,z<a?,则基于w的瑞利分布的随机数发生器z的方程为 z = a + ? b l n ( 1 ? w ) z=a+\sqrt{-bln(1-w)} z=a+?bln(1?w)?
- 若高斯低通滤波器在频域中的表示为 H ( u , v ) = e ? D 2 ( u , v ) 2 D 0 2 H(u,v)=e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} H(u,v)=e?2D02?D2(u,v)?则对应的高斯高通滤波器在频域中的表示为 H h ( u , v ) = 1 ? e ? D 2 ( u , v ) 2 D 0 2 H_{h}(u,v)=1-e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} Hh?(u,v)=1?e?2D02?D2(u,v)?
- Weiner 滤波的计算方法为 F ( u , v ) = [ 1 H ( u , v ) ? ∣ H ( u , v ) ∣ 2 ∣ H ( u , v ) ∣ 2 + S η ( x , y ) S f ( x , y ) ] G ( u , v ) ) F(u,v)=[\frac{1}{H(u,v)}·\frac{|H(u,v)|^{2}}{|H(u,v)|^{2}+\frac{S_{\eta }(x,y)}{S_{f}(x,y)}}]G(u,v)) F(u,v)=[H(u,v)1??∣H(u,v)∣2+Sf?(x,y)Sη?(x,y)?∣H(u,v)∣2?]G(u,v))其中 S η ( x , y ) S_{\eta }(x,y) Sη?(x,y)代表噪声功率谱密度,H(u,v)代表退化函数
- YCbCr中的Y代表明度,Cb与Cr代表蓝色与红色的浓度偏移,HSV中的H代表色调,s代表饱和度
二、选择
-
采用对比度拉伸是实现灰度图像的增强的一种重要思路,而分段线性变换函数是一种常被采用的技术。针对某一段输入灰度范围,若你想扩大输出灰度的动态范围,所构造的那一段线性映射函数的斜率k应满足:(A)
A.k>1
B.k=1
C.k<1
D.取任何值都可以 -
若一幅图像中存在椒盐噪声,下面哪种滤波器可选择来去除它们:(D)
A.算术均值滤波器
B.反调和滤波器
C.拉普拉斯滤波器
D.中值滤波器 -
通过卷积运算对图像进行各种目的的滤波是图像处理的重要内容。对于离散的两个一维信号[3,5,6],g=[1,-1],对应的卷积结果是(A)
A.[3,2,1,-6]
B.[2.1]
C.[-3,-2-1,6]
D.[-2,-1] -
高斯低通滤波器 H ( u , v ) = e ? D 2 ( u , v ) 2 D 0 2 H(u,v)=e^{-\frac{D^{2}(u,v)}{2D_{0}^{2}}} H(u,v)=e?2D02?D2(u,v)?中存在一个参数 D 0 D_{0} D0?,对于一幅中年妇女面部特写图像,若发现采用 D 0 = 100 D_{0}=100 D0?=100时,去除该妇女眼部的皱纹不彻底,则应该:(A)
A.适当减小 D 0 D_{0} D0?
B.适当加大 D 0 D_{0} D0?
C.保持 D 0 D_{0} D0?不变
D.前面选项都不对 -
对于一个具有正交性质的完美重建滤波器组,若它的滤波器之间具有如下的关系:(B)
g 1 ( n ) = ( ? 1 ) n g 0 ( 2 K ? 1 ? n ) , h 1 ( n ) = g 1 ( 2 K ? 1 ? n ) , i = 0 , 1 g_{1}(n)=(-1)^{n}g_{0}(2K-1-n),h_{1}(n)=g_{1}(2K-1-n),i=0,1 g1?(n)=(?1)ng0?(2K?1?n),h1?(n)=g1?(2K?1?n),i=0,1A. ( ? 1 ) n h 0 ( 2 K ? 1 ? n ) (-1)^{n}h_{0}(2K-1-n) (?1)nh0?(2K?1?n)
B. ( ? 1 ) n + 1 h 0 ( 2 K ? 1 ? n ) (-1)^{n+1}h_{0}(2K-1-n) (?1)n+1h0?(2K?1?n)
C. ( ? 1 ) n h 0 ( n ) (-1)^{n}h_{0}(n) (?1)nh0?(n)
D. ( ? 1 ) n + 1 h 0 ( n ) (-1)^{n+1}h_{0}(n) (?1)n+1h0?(n) -
信息论是信息压缩的理论基础,而互信息是信息论中一个非常重要的概念,信源z与信道输出v之间互信息I(z,v)的意义为?
A.信源z与信道输出v间的平均信息量
B.观察单一信道输出符号时接收到的平均信息
C.观测到输出v后信源符号的平均信息量
D信道可靠传输信息的最大传送率
三、判断
- 对一幅数字图像进行一次直方图均衡处理后,通常不会产生非常绝对平的直方图。即便我们对处理后的图像再进行一次直方图处理,理论上也不会产生任何效果。(√)
- 拉普拉斯滤波器与统计排序滤波器均不是一种卷积运算。(×)
- 卷积运算具有交换性与结合性。(√)
- 低通高阶巴特沃斯滤波器存在振铃效应,而低通高斯滤波器不存在振铃效应。(√)
- 我们可以用阶数Q<0的逆谐波均值滤波器来去除盐噪声。(√)
- 给定一幅图像,若我们能准确估计噪声的均值与方差,则可以知道噪声的能量(所有像素位置的噪声强度的平方和)。(√)
- 在图像编码中,涉及信源编码与信道编码,两者都是为了实现信息的压缩表示。(×)
- 对于一个事件,它发生的概率越小,它的熵越大。(√)
- 若一幅图像中含有一些噪声点或干扰性微小结构,可采用形态处理中的开操作作为一种处理段来去除它。(√)
四、简答
1. 简述什么是线性移不变系统
答:线性移不变性系统(Linear Shift-Invariant System,简称LSI系统)是一种特殊的系统,它对输入图像的处理满足线性和移不变性两个条件。
- 线性:系统对输入图像的处理是线性的,即如果输入图像是两个图像的线性组合,那么输出图像也是这两个图像经过系统处理后的输出的相同线性组合。数学上表示为,如果 f 1 ( x , y ) f_{1}(x,y) f1?(x,y)和 f 2 ( x , y ) f_{2}(x,y) f2?(x,y)是两个输入图像,α和β是任意常数,那么系统的输出满足: S ( α f 1 + β f 2 ) = α S ( f 1 ) + β S ( f 2 ) S(αf_{1}+βf_{2})=αS(f_{1})+βS(f_{2}) S(αf1?+βf2?)=αS(f1?)+βS(f2?)
- 移不变性:系统对输入图像的处理是移不变的,即如果输入图像在空间域内平移,那么输出图像也会相应地平移,而不会改变其它特性。数学上表示为,如果f(x,y)是输入图像, ( x 0 , y 0 ) (x_{0},y_{0}) (x0?,y0?)是平移量,那么系统的输出满足: H [ f ( x , y ) ] = g ( x , y ) , H [ f ( x ? x 0 , y ? y 0 ) ] = g ( x ? x 0 , y ? y 0 ) H[f(x,y)]=g(x,y),H[f(x-x_{0},y-y_{0})]=g(x-x_{0},y-y_{0}) H[f(x,y)]=g(x,y),H[f(x?x0?,y?y0?)]=g(x?x0?,y?y0?)
线性移不变性系统的一个重要特性是,它们可以通过卷积运算来描述。对于任何LSI系统,都存在一个称为系统冲激响应的函数 h ( x , y ) h(x,y) h(x,y),使得系统对任何输入图像 f ( x , y ) f(x,y) f(x,y) 的输出 g ( x , y ) g(x,y) g(x,y)可以表示为 f ( x , y ) f(x,y) f(x,y)和 h ( x , y ) h(x,y) h(x,y)的卷积: g ( x , y ) = f ( x , y ) ? h ( x , y ) g(x,y)=f(x,y)\ast h(x,y) g(x,y)=f(x,y)?h(x,y)
2. 观察如下所示图像。右边的图像这样得到:
(a)在原始图像左边乘以
(
?
1
)
x
+
y
(-1)^{x+y}
(?1)x+y;
(b) 计算离散傅里叶变换(DFT);
? 对变换取复共轭;
(d) 计算傅里叶反变换;
(e) 结果的实部再乘以
(
?
1
)
x
+
y
(-1)^{x+y}
(?1)x+y。
(用数学方法解释为什么会产生右图的效果)。DIP旋转了180度
假设原图像为 f 1 ( x , y ) f_{1}(x,y) f1?(x,y)
- 经过a操作变为 ( ? 1 ) x + y f 1 ( x , y ) (-1)^{x+y}f_{1}(x,y) (?1)x+yf1?(x,y)
- 经过b操作离散傅里叶变换变为 F ( u , v ) = 1 M N ∑ u = 0 M ? 1 ∑ v = 0 N ? 1 ( ? 1 ) x + y f ( x , y ) e ? j 2 π ( u x M + u y N ) F(u,v)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{-j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}} F(u,v)=MN1?∑u=0M?1?∑v=0N?1?(?1)x+yf(x,y)e?j2π(Mux?+Nuy?)
- 通过c操作,根据傅里叶变换性值
- F ? ( u , v ) = 1 M N ∑ u = 0 M ? 1 ∑ v = 0 N ? 1 ( ? 1 ) x + y f ( x , y ) e j 2 π ( u x M + u y N ) F^\ast (u,v)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}} F?(u,v)=MN1?∑u=0M?1?∑v=0N?1?(?1)x+yf(x,y)ej2π(Mux?+Nuy?)
- 通过d操作得傅里叶反变换变为
- I D F T ( F ? ( u , v ) ) = 1 M N ∑ u = 0 M ? 1 ∑ v = 0 N ? 1 [ 1 M N ∑ u = 0 M ? 1 ∑ v = 0 N ? 1 ( ? 1 ) x + y f ( x , y ) e j 2 π ( u x M + u y N ) ] e j 2 π ( u x M + u y N ) IDFT(F^\ast (u,v))=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}[\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{(-1)^{x+y}f(x,y)e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)}}]e^{j2\pi\left(\frac{ux}{M}+\frac{uy}{N}\right)} IDFT(F?(u,v))=MN1?∑u=0M?1?∑v=0N?1?[MN1?∑u=0M?1?∑v=0N?1?(?1)x+yf(x,y)ej2π(Mux?+Nuy?)]ej2π(Mux?+Nuy?)实部为 ( ? 1 ) x + y f ( ? x , ? y ) (-1)^{x+y}f(-x,-y) (?1)x+yf(?x,?y)
- e操作后变为
(
?
1
)
x
+
y
(
?
1
)
x
+
y
f
(
?
x
,
?
y
)
=
f
(
?
x
,
?
y
)
(-1)^{x+y}(-1)^{x+y}f(-x,-y)=f(-x,-y)
(?1)x+y(?1)x+yf(?x,?y)=f(?x,?y)
效果原图像旋转180°
3. 描述如何构建高斯金字塔与拉普拉斯金字塔
-
高斯金字塔建立:
- 生成初始图像(最底层): 将原始图像 f ( x , y ) f(x,y) f(x,y)作为金字塔的第一层。
- 进行下采样: 对当前层的图像进行高斯滤波,然后进行下采样,即去除一些行和列,以生成下一层的图像。下采样可以使用像素平均值或其他插值技术。下采样的目的是减小图像的尺寸。
- 重复步骤2: 重复进行高斯滤波和下采样,直到达到金字塔的顶层。每一层的图像尺寸都比前一层的尺寸小。
-
拉普拉斯金字塔建立:
- 生成高斯金字塔: 使用上述方法生成高斯金字塔。
- 构建拉普拉斯金字塔: 拉普拉斯金字塔的每一层都是由对应的高斯金字塔层与该层的上一层进行差分得到的。即,拉普拉斯金字塔的每一层是由高斯金字塔的对应层减去该层的上一层。对于每一层i,拉普拉斯金字塔的图像
L
i
L_{i}
Li?可以用以下公式表示:
L
i
=
G
i
?
e
x
p
a
n
e
d
(
G
i
+
1
)
L_{i}=G_{i}-expaned(G_{i+1})
Li?=Gi??expaned(Gi+1?)
其中, G i G_{i} Gi?是高斯金字塔的第 i 层,expaned是上采样操作。这样,我们得到的拉普拉斯金字塔的第一层是高斯金字塔的最顶层,最后一层是高斯金字塔的最底层
4. 每一个小波的尺度函数都遵循Mallat提出的多分辨率分析的4个基本要求,请描述这4个基本要求的内容
答:
- 尺度函数对它的整数平移对应的函数是正交的
- 哈尔函数被称为是紧支撑的,意味着除了称为支撑域有限区间外,函数值都为0
- 必须注意,当尺度函数的支撑域大于1时,整数平移函数间的正交性将变得更加难于被满足 - 低尺度尺度函数张成的子空间包含于高尺度尺度函数张成的子空间内
V ? ∞ ? . . . ? V ? 1 ? V ? 0 ? V 1 ? . . . ? V + ∞ V_{-∞} \subset ... \subset V_{-1}\subset V_{-0}\subset V_{1}\subset ...\subset V_{+∞} V?∞??...?V?1??V?0??V1??...?V+∞? - 唯一包含在
V
j
V_{j}
Vj?所有中的函数是f(x)=0
V ? ∞ = 0 V_{-∞}=0 V?∞?=0 - 任何函数都可以以任意精度表示 V ∞ = L 2 ( R ) V_{∞}=L^{2}(R) V∞?=L2(R)
5. 傅里叶变换的6个性质
- 空域频移性 F [ f ( x ? x 0 , y ? y 0 ) ] = F ( u , v ) e ? j 2 π ( u x 0 M + v y 0 N ) \mathscr{F}[f(x-x_{0},y-y_{0})]=F(u,v)e^{-j2\pi (\frac{ux_{0}}{M}+\frac{vy_{0}}{N})} F[f(x?x0?,y?y0?)]=F(u,v)e?j2π(Mux0??+Nvy0??)
- 时域频移性
F
[
f
(
x
,
y
)
e
?
j
2
π
(
u
x
0
M
+
v
y
0
N
)
]
=
F
(
u
?
u
0
,
v
?
v
0
)
\mathscr{F}[f(x,y)e^{-j2\pi (\frac{ux_{0}}{M}+\frac{vy_{0}}{N})}]=F(u-u_{0},v-v_{0})
F[f(x,y)e?j2π(Mux0??+Nvy0??)]=F(u?u0?,v?v0?)
- F [ f ( x , y ) ( ? 1 ) x + y ] = F ( u ? M 2 , v ? N 2 ) \mathscr{F}[f(x,y)(-1)^{x+y}]=F(u-\frac{M}{2},v-\frac{N}{2}) F[f(x,y)(?1)x+y]=F(u?2M?,v?2N?) - 平均和对称
- 平均 F ( 0 , 0 ) = 1 M N ∑ u = 0 M ? 1 ∑ v = 0 N ? 1 f ( x , y ) F(0,0)=\frac{1}{MN}\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}{f(x,y)} F(0,0)=MN1?∑u=0M?1?∑v=0N?1?f(x,y)
- 共轭 F ( u , v ) = F ? ( ? u , ? v ) F(u,v)=F^{\ast}(-u,-v) F(u,v)=F?(?u,?v)
- 对称 ∣ F ( u , v ) ∣ = ∣ F ( ? u , ? v ) ∣ |F(u,v)|=|F(-u,-v)| ∣F(u,v)∣=∣F(?u,?v)∣
- 可分离性 F ( u , v ) = F f ( x , y ) = ∑ y [ ∑ x f ( x , y ) e ? j 2 π x u M ] e ? j 2 π y v N = ∑ y F ( u , y ) e ? j 2 π y v N F(u,v)=\mathscr{F}f(x,y)=\sum_{y}[\sum_{x}{f(x,y)e^{-j2\pi \frac{xu}{M}}}]e^{-j2\pi \frac{yv}{N}}=\sum_{y}F(u,y)e^{-j2\pi \frac{yv}{N}} F(u,v)=Ff(x,y)=∑y?[∑x?f(x,y)e?j2πMxu?]e?j2πNyv?=∑y?F(u,y)e?j2πNyv?
- 旋转性
x
=
r
c
o
s
θ
,
y
=
r
s
i
n
θ
,
u
=
ω
c
o
s
φ
,
v
=
ω
s
i
n
φ
x=rcosθ ,y=rsinθ , u=\omega cos\varphi , v=\omega sin\varphi
x=rcosθ,y=rsinθ,u=ωcosφ,v=ωsinφ
f ( r , θ + θ 0 ) ? F ( ω , φ + θ 0 ) f(r,θ+θ_{0})\Leftrightarrow F(\omega,\varphi+θ_{0}) f(r,θ+θ0?)?F(ω,φ+θ0?) - 周期性f(x,y)=f(x+M,y)=f(x,y+N)=f(x+M,y+N)
F(u,v)=F(u+M,v)=F(u,v+N)=F(u+M,v+N) - 线性 F ( a f ( x , y ) + b g ( x , y ) ) = a F ( f ( x , y ) ) + b F ( g ( x , y ) ) \mathscr{F} (af(x,y)+bg(x,y))=a\mathscr{F} (f(x,y))+b\mathscr{F}(g(x,y)) F(af(x,y)+bg(x,y))=aF(f(x,y))+bF(g(x,y))
- 微分性
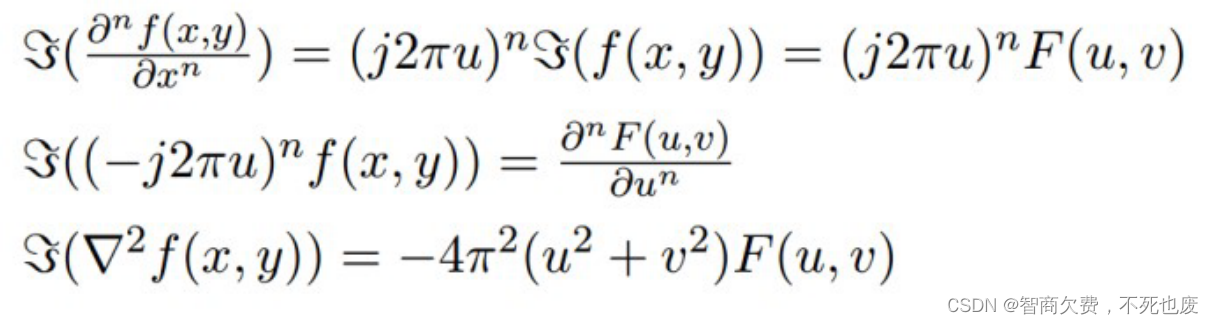
6. 请用集合的语言描述形态学中的腐蚀与膨胀,并用进一步用数学公式定义开运算与闭运算。
假设 A 是一个图像集合,并且 B 是一个称为结构元素的集合。
-
腐蚀(Erosion):
腐蚀操作可以看作是将结构元素 B 从图像 A 中滑动,只要 B 完全覆盖A 的某一部分,那么该部分就被保留,否则就被去除。
数学表述为: A ? B = { z ∣ ( B ) z ? A } A?B=\left \{ z∣(B)_{z}\subseteq A \right \} A?B={z∣(B)z??A}
? 表示腐蚀操作, ( B ) z (B)_{z} (B)z?表示将结构元素 B 的原点放在 z 处。 -
膨胀(Dilation):
膨胀操作可以看作是将结构元素 B 从图像 A 中滑动,只要B 与 A 有交集,那么该部分就被保留。
数学表述为: A ⊕ B = { z ∣ ( B ) z ? A } A⊕B=\left \{ z∣(B)_{z}\subseteq A \right \} A⊕B={z∣(B)z??A}⊕ 表示膨胀操作 -
开运算(Opening):
开运算首先对图像进行腐蚀,然后再进行膨胀。这通常用于消除小的对象或噪声。
数学表述为: A ° B = ( A ⊕ B ) ? B A°B=(A⊕B)?B A°B=(A⊕B)?B -
闭运算(Closing):
闭运算首先对图像进行膨胀,然后再进行腐蚀。这通常用于填充小的孔洞或连接不连续的对象。
数学表述为: A ? B = ( A ? B ) ⊕ B A·B=(A?B)⊕B A?B=(A?B)⊕B
7. 简述拉普拉斯算子、拉普拉斯算子的傅里叶变换?
五、计算
1.直方图均衡
一幅具有8个灰度级的图像的归一化直方图为[0.17 0.25 0.21 0.16 0.07 0.08 0.04 0.02],求直方图均衡后的灰度级和对应概率,并画出均衡后归一化直方图的示意图。
2. Z 变换证明
Z变换是一种信号分析的重要工具。它有许多重要的性质,请对如下性质进行证明:
- (1)若x(n)的Z变换为X(z),则 ( ? 1 ) n x ( n ) (-1)^{n}x(n) (?1)nx(n)的Z变换为 X(-z)
- (2)若x(n)的Z变换为X(z),则 x(-n)的Z变换为 X ( 1 z ) X(\frac{1}{z}) X(z1?)
- (3)若x(n)的Z变换为X(z),则下x(2n)的Z变换为
1
2
[
X
(
z
1
2
)
+
X
(
?
z
1
2
)
]
\frac{1}{2}[X(z^\frac{1}{2})+X(-z^\frac{1}{2})]
21?[X(z21?)+X(?z21?)]
证明:已知x(n)的Z变换为: X ( Z ) = ∑ ? ∞ ∞ x ( n ) z ? n X(Z)=\sum_{-\infty}^{\infty}{x(n)z^{-n}} X(Z)=∑?∞∞?x(n)z?n-
( ? 1 ) n x ( n ) {(-1)}^nx(n) (?1)nx(n)的Z变换为:
∑ ? ∞ ∞ ( ? 1 ) n x ( n ) z ? n = ∑ ? ∞ ∞ ( ? 1 ) ? n x ( n ) z ? n = ∑ ? ∞ ∞ x ( n ) ( ? z ) ? n = X ( ? z ) \sum_{-\infty}^{\infty}{\left(-1\right)^{n}x\left(n\right)z^{-n}}=\sum_{-\infty}^{\infty}{\left(-1\right)^{-n}x\left(n\right)z^{-n}}=\sum_{-\infty}^{\infty}{x\left(n\right)\left(-z\right)^{-n}}=X\left(-z\right) ∑?∞∞?(?1)nx(n)z?n=∑?∞∞?(?1)?nx(n)z?n=∑?∞∞?x(n)(?z)?n=X(?z) -
x(-n)的Z变换为:
∑ ? ∞ ∞ x ( ? n ) z ? ( ? n ) = ∑ ? ∞ ∞ x ( ? n ) ( z ? 1 ) ? n = X ( z ? 1 ) = X ( 1 Z ) \sum_{-\infty}^{\infty}{x\left(-n\right)z^{-(-n)}}=\sum_{-\infty}^{\infty}{x\left(-n\right)\left(z^{-1}\right)^{-n}}=X\left(z^{-1}\right)=X\left(\frac{1}{Z}\right) ∑?∞∞?x(?n)z?(?n)=∑?∞∞?x(?n)(z?1)?n=X(z?1)=X(Z1?)
x(2n)的Z变换为
∑ ? ∞ ∞ x ( 2 n ) z ? n \sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}} ∑?∞∞?x(2n)z?n
令 k = 2 n k=2n k=2n
有 ∑ ? ∞ ∞ x ( 2 n ) z ? n = ∑ ? ∞ ∞ x ( k ) z ? k 2 \sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}}=\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}} ∑?∞∞?x(2n)z?n=∑?∞∞?x(k)z?2k?
将 X ( z 1 2 ) = ∑ ? ∞ ∞ x ( k ) z ? k 2 X(z^{\frac{1}{2}})=\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}} X(z21?)=∑?∞∞?x(k)z?2k?
X ( z ? 1 2 ) = ∑ ? ∞ ∞ x ( k ) ( ? 1 ) k z ? k 2 X(z^{-\frac{1}{2}})=\sum_{-\infty}^{\infty}{x\left(k\right)(-1)^{k}z^{-\frac{k}{2}}} X(z?21?)=∑?∞∞?x(k)(?1)kz?2k?相加得
1 2 [ X ( z 1 2 ) + X ( ? z 1 2 ) ] = ∑ ? ∞ ∞ x ( k ) z ? k 2 + ∑ ? ∞ ∞ x ( k ) ( ? 1 ) k z ? k 2 = ∑ ? ∞ ∞ x ( 2 n ) z ? n \frac{1}{2}[X(z^\frac{1}{2})+X(-z^\frac{1}{2})]\\ =\sum_{-\infty}^{\infty}{x\left(k\right)z^{-\frac{k}{2}}}+\sum_{-\infty}^{\infty}{x\left(k\right)(-1)^{k}z^{-\frac{k}{2}}}\\=\sum_{-\infty}^{\infty}{x\left(2n\right)z^{-n}} 21?[X(z21?)+X(?z21?)]=∑?∞∞?x(k)z?2k?+∑?∞∞?x(k)(?1)kz?2k?=∑?∞∞?x(2n)z?n
-
3. 拉普拉斯旋转不变性证明
形式化描述什么是拉普拉斯算子,并证明拉普拉斯算子具有旋转不变性质
(二维平面内的旋转变换计算公式为
x
′
=
x
c
o
s
θ
?
y
s
i
n
θ
,
y
=
x
s
i
n
θ
+
y
c
o
s
θ
x'=xcosθ-ysinθ,y=xsinθ+ycosθ
x′=xcosθ?ysinθ,y=xsinθ+ycosθ)
证明:

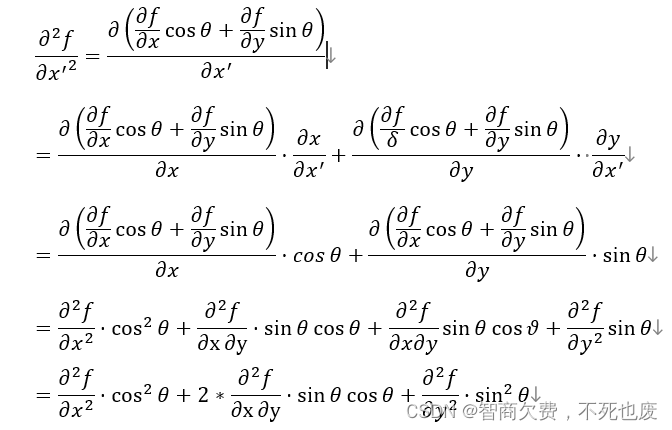
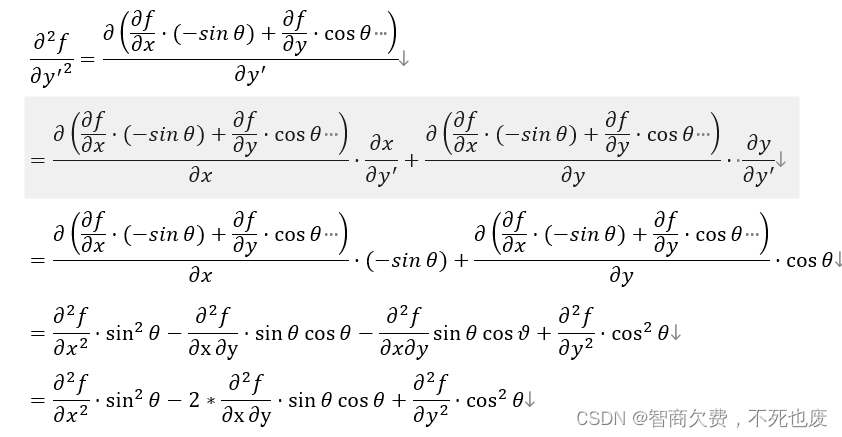

4.推导出随机数生成方程
假设我们有一个[0,1]上的均匀分布随机数发生器U(0,1), 请基于它构造指数分布的随机数发生器,推导出随机数生成方程。
若我们有一个标准正态分布的随机数发生器N(0,1),请推导出对数正态分布的随机数生成方程。
解: (1) 设U(0,1)可生成随机数
w
∈
[
0
,
1
]
w\in [0,1]
w∈[0,1],用它生成具有指数分布的随机数z,则其分布具有形式
F
(
z
)
=
1
?
e
?
a
z
,
z
≥
0
F(z)=1-e^{-az},z\ge 0
F(z)=1?e?az,z≥0
令F(z)=w,解得:
z
=
?
1
a
l
n
[
1
?
U
(
0
,
1
)
]
z=-\frac{1}{a}ln[1-U(0,1)]
z=?a1?ln[1?U(0,1)]
(2) 设N(0,1)可生成随机数
w
∈
[
0
,
1
]
w\in [0,1]
w∈[0,1],用它生成具有正态分布的随机数z,则其分布具有形式
F
(
z
)
=
∫
0
z
1
2
π
b
F(z)=\int_{0}^{z}\frac{1}{\sqrt{2\pi b}}
F(z)=∫0z?2πb?1?
e
?
[
l
n
(
v
)
?
a
]
2
2
b
2
d
v
e^{-\frac{[ln(v)-a]^{2}}{2b^{2}}}dv
e?2b2[ln(v)?a]2?dv
令F(z)=w,解得:
z
=
e
b
w
+
a
z=e^{bw+a}
z=ebw+a
即
z
=
e
b
N
(
0
,
1
)
+
a
z=e^{bN(0,1)+a}
z=ebN(0,1)+a
5. 快速小波变换分解与重建
在分析信号时小波分解与重建是一个重要的工具,离散 haar 小波是一种重要而简单J1/5 n=0.1的小波,它的尺度与小波向量分别为
- (1)现在假设我们有一个长度为8的信号f[1,-3,3,1,2,0,-2,1],利用快速哈尔小波变换进行三层的分解,计算各层的滤波器输出。
- (2)若利用哈尔小波对某个信号进行三层的分解的滤波器输出
W = [ W φ ( 1 , 0 ) , W φ ( 1 , 0 ) , W φ ( 2 , 0 ) , W φ ( 2 , 1 ) , W φ ( 3 , 0 ) , W φ ( 3 , 1 ) , W φ ( 3 , 2 ) , W φ ( 3 , 3 ) ] = [ 1 , 1 , ? 1 , ? 1 , 1 , 0 , 1 , 0 ] W=[W_{\varphi }(1,0),W_{\varphi }(1,0),W_{\varphi }(2,0),W_{\varphi }(2,1),W_{\varphi }(3,0),W_{\varphi }(3,1),W_{\varphi }(3,2),W_{\varphi }(3,3)]=[ 1,1,-1,-1,1,0,1,0] W=[Wφ?(1,0),Wφ?(1,0),Wφ?(2,0),Wφ?(2,1),Wφ?(3,0),Wφ?(3,1),Wφ?(3,2),Wφ?(3,3)]=[1,1,?1,?1,1,0,1,0],请计算重建原来的信号。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- npm run start启动时提示 A decorated export must export a class declaration报错
- Ansible:简单、快速、安全、最强大的 IT 自动化系统 | 开源日报 No.140
- 第六章 树和二叉树
- TCP的这些特性你知道吗?(滑动窗口篇)
- sqlite_orm学习笔记
- iconfont拓展iview图标库
- Oracle Linux 8.9 安装图解
- LeetCode刷题--- 组合总和
- 课后拓展作业
- 四款通用组织架构图模板-一键高清导出