YOLOv3：算法与论文详细解读

【yolov1：背景介绍与算法精讲】
【yolo9000：Better, Faster, Stronger的目标检测网络】

一、YOLOv3概述

YOLOv3是YOLO系列目标检测算法的第三个版本，由Joseph Redmon和Alexey Bochkovskiy于2018年发布。在YOLOv2的基础上进行了改进，引入了一系列的变化以提高检测性能。在该论文中最主要的就是需要去理解它的网络结构，像残差链接、多尺度训练这两块内容，因为在原论文中相关细节其实说的并不清楚，所以自己在网上查阅了很多相关资料才能理解网络的设计思路与详细细节。

原论文传送门：【YOLOv3: An Incremental Improvement】

二、创新与改进

YOLOv3的创新与改进主要有以下几点：

• 进行多尺度训练，网络输出三个尺度的feature map
• 设计了新的网络结构，使用FPN网络特征金字塔进行特征融合，添加了残差连接模块
• 在分类部分使用了Logistic来代替之前的softmax

三、改进细节

3.1 多尺度特征

在详细介绍YOLOV3多尺度特征之前我们先来看一下YOLOV1和YOLOV2的特征图输出结构。
yolov1 输入输出
YOLOV1输入的图像在经过网络输出之后，输出的是7x7x30的特征向量参数，详细参数请移步YOLOV1文章中，

yolov2 输入输出
在YOLOv2论文中，图像输入到Darknet-19网络后，经过32倍下采样之后输出的是13x13x5x25，具体细节可以参考yolov2算法解读文章。

YOLOV3特征图输出
在yolov3输出不再是一个尺度的feature map,而是三个尺度，分别是经过32倍下采样、16倍下采样、8倍下采样的特征图。

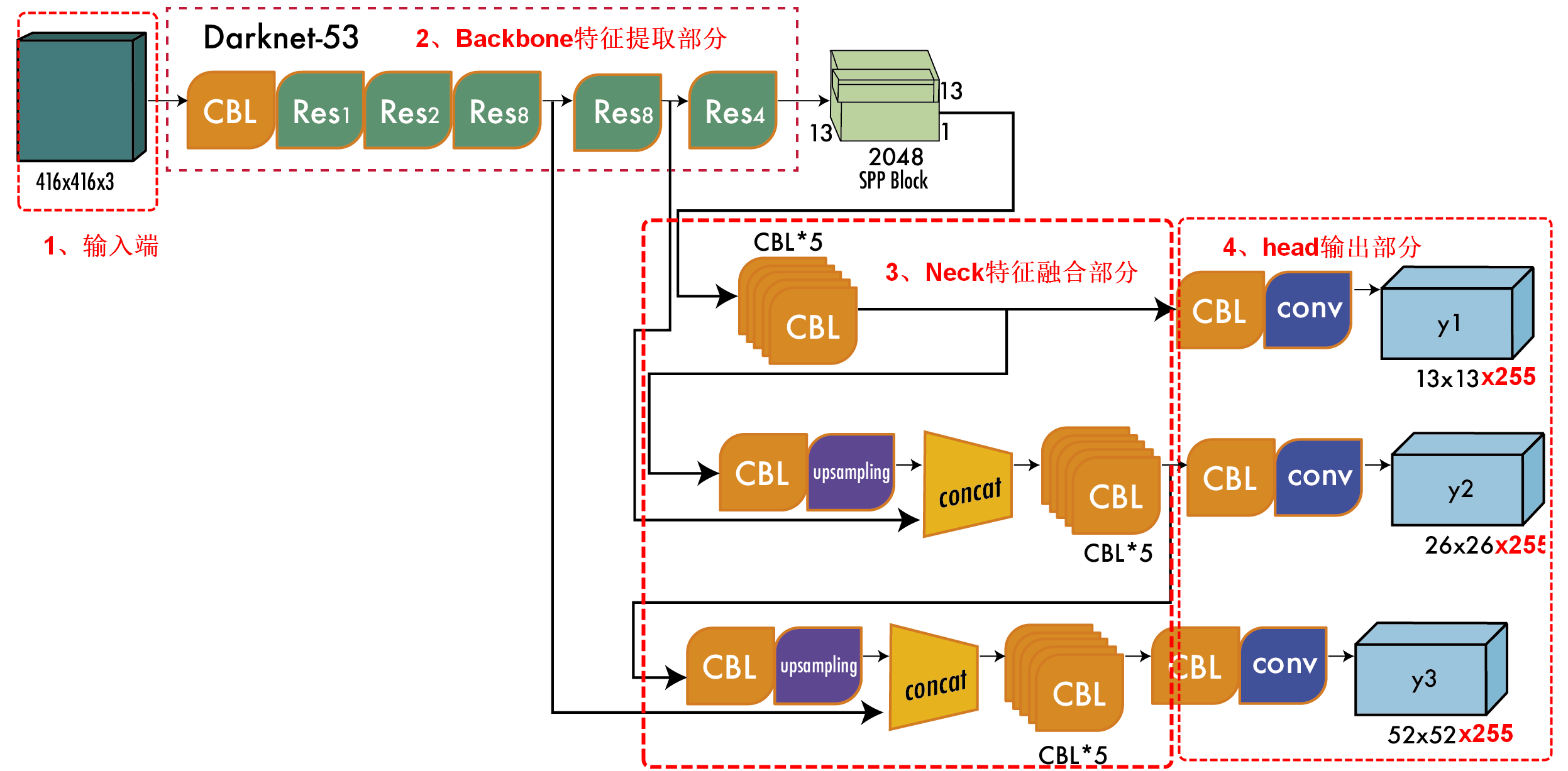
详细实现细节可以参考这幅图，416x416x3的图像在经过特征提取网络和残差连接之后输出了三个尺度的特征图，再经过32倍、16倍、8倍下采样之后获得的分别是13x13x255，26x26x255、52x52x255特征图，这三个参数分别代表含义已经在上面这幅图展示出来了。

13x13表示生成的grid cell数，每个grid cell生成3个anchor(这一块和yolov2不一样，v2每个grid cell生成的是5个anchor)，每个anchor包含边框坐标、边界框置信度、对象类别数，yolov3训练使用的是MS COCO数据集一共80个类别。

3.2 不同尺度先验框

为什么要使用多尺度特征呢，因为我们在yolov1和yolov2训练过程中会发现很多小目标的物体无法被识别，在yolov3中生成的三个尺度的特征可以识别大目标、中目标、小目标。

---

分配上，在最小的13x13特征图上 （有最大的感受野） 应用较大的先验框，适合检测较大的对象。中等的26x26特征图上 （中等感受野） 应用中等的先验框，适合检测中等大小的对象。较大的52x52特征图上 （较小的感受野） 应用较小的先验框适合检测较小的对象。

随着输出的特征图的数量和尺度的变化，先验框的尺寸也需要相应的调整。YOLO2已经开始采用K-means聚类得到先验框的尺寸，YOLO3延续了这种方法，为每种下采样尺度设定3种先验框，总共聚类出9种尺寸的先验框。在COCO数据集这9个先验框是：(10x13)，(16x30)，(33x23)，(30x61)，(62x45)，(59x119)，(116x90)，(156x198)，(373x326)。

3.3 完整的网络结构

完整的YOLOv3网络是由4个部分组成：输入层、Backbone特征提取部分，也就是Darknet-53，Neck特征拼接部分，head头分类部分。

• Backbone主干网络负责从输入图像中提取有用的特征。它通常是在大规模图像分类任务（例如 ImageNet）上训练的卷积神经网络 (CNN)。主干网捕获不同尺度的层次特征，在较早的层中提取较低级别的特征（例如边缘和纹理），在较深层中提取较高级别的特征（例如对象部分和语义信息）。
• Neck颈部是连接脊柱和头部的中间部件。它聚合和细化主干提取的特征，通常侧重于增强不同尺度的空间和语义信息。颈部可能包括额外的卷积层、特征金字塔网络（FPN）或其他机制来改善特征的表示。
• head头部是物体探测器的最后一个部件；它负责根据主干和颈部提供的特征进行预测。它通常由一个或多个特定于任务的子网络组成，这些子网络执行分类、定位以及最近的实例分割和姿势估计。头部处理颈部提供的特征，为每个候选对象生成预测。最后，后处理步骤（例如非极大值抑制 (NMS)）会过滤掉重叠的预测，并仅保留最置信度的检测。
  

3.3 Darknet-53主干网络

YOLOv3 Darknet-53 主干网。 YOLOv3 的架构由 53 个卷积层组成，每个层都具有批量归一化和 Leaky ReLU 激活功能。此外，残差连接将整个网络中 1 × 1 卷积的输入与 3 × 3 卷积的输出连接起来。此处所示的架构仅包含主干；不包括多尺度预测组成的检测头。虚框中每两个卷积之后就会进行一次Residual残差连接，右边的x8、x4表示当前模块的个数。

3.4 残差网络

很多博主只是说了残差结构，但是并没有说明为什么要使用残差，在学习残差网络之前一定要学习两个概念：恒等映射和网络退化

3.4.1 恒等映射

恒等映射（Identity Mapping）是指将输入直接映射到输出，不进行任何变换或处理的映射方式。在神经网络中，恒等映射常常与残差连接（Residual Connection）一起使用。

考虑一个神经网络的层，用数学表示为 (F(x))，其中 (x) 是输入，(F) 是网络的变换。恒等映射的形式是 (F(x) = x)，即输入直接等于输出。残差连接通过引入跳跃连接，将输入直接添加到输出中，即 (H(x) = F(x) + x)。

残差连接的思想是，如果网络学到的变换是恒等映射，那么网络就可以轻松地学到一个接近零的残差。这样的设计有助于缓解深层网络中的梯度消失问题，促使网络更容易学习有效的表示。

在深度残差网络（Residual Networks，ResNets）中，这种结构被广泛使用。ResNet的基本块由两个路径组成，一个是普通的网络变换路径，另一个是恒等映射的路径，两者相加形成输出。这种设计使得神经网络在学习过程中可以选择性地使用恒等映射，从而更容易训练深层网络。

总的来说，恒等映射在神经网络中的应用是为了促使网络更容易学习恒等变换，以改善训练的稳定性和效果。

3.4.2 网络退化

常规思考：越深的网络拟合能力越强，因此越深的网络训练误差应该越低，但实际相反。随着网络的加深，模型训练的精度下降。

原因：并非过拟合问题，而是网络优化比较困难。这个时候就是需要想办法让深层网络的性能逼近浅层网络。

3.4.3 残差结构

首先看一下普通网络和残差网络的一个差异，后面解释过程中会用到一些名词，分别是：
Plain network：普通结构网络
Building block：组件，数个网络层构成的固定系列操作
普通网络

Plain network：Block_out = H（x）

残差网络

Residual learning：Block_out = H（x） = F（x）+ x

我们残差学习的目的是让网络层拟合H(x)-x，也就是F(x)， 而非H(x)

先思考以下几个残差相关的问题

问：为什么拟合F(x)?
答：提供building block更容易学到**恒等映射（identity mapping）**的可能

问：为什么拟合F（x）就使得building block容易学到恒等映射？
答:在深度学习中，通过拟合 F(x) = H(x) - x)（即残差）的形式，模型变得更容易学到恒等映射。这是因为对于 H(x)学习到的变换，如果 H(x)本身就接近于恒等映射，那么 F(x) = H(x) - x 的残差项就会趋近于零。考虑一个深层网络的建筑块，其中 H(x) 表示网络的变换，x 是输入。如果 H(x) 学到的是一个接近于恒等映射的变换，那么 H(x) - x 的残差项就会接近零。这使得训练更容易，因为模型只需要学到微小的调整，而不是复杂的映射。具体来说，如果 H(x) 学到了有效的特征表示，那么 F(x) = H(x) - x 中的 H(x) 就趋近于 (x)，使得 F(x) 接近于零。这就相当于告诉模型：“如果你学到的是一个有效的表示，就尽量保持输入和输出相同，不要进行太多的变换。”这种设计使得模型更容易训练，因为它不需要从零开始学习复杂的映射。

问：为什么要恒等映射？
答：让深层网络不至于比浅层网络差

3.4.4 残差的两个堆叠形式

注意：残差连接只有大小维度完全相同的两个feature map才能进行残差连接。

第一种Basic：两个3x3卷积堆叠
第二种Bottleneck：利用1x1卷积减少计算量

Bottleneck
第一个1x1下降1/4通道数
第二个1x1提升4倍通道数

3.4.5 YOLOV3中的残差连接

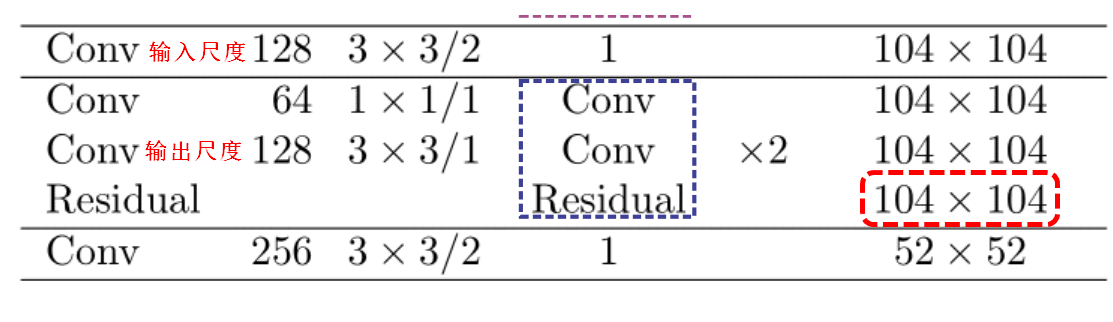
在yolov3中一共进行了5次残差连接，这里以第二次残差连接举例，在进入残差模块之前我们输入的特征图是104x104x128，在经过一次1x1卷积和一次3x3卷积之后，输出的特征图维度104x104x128，将输入特征与输出特征进行残差连接得到的特征图为104x104x128，残差连接之后特征图的尺寸不会发生变化。

3.5 head输入部分

yolov3依旧使用的全卷积网络结构，所以可以进行多尺度图片输入，不同的图片输入最后得到的特征图尺寸也不一样，但是需要注意，因为生成的3个尺度的feature map分别是经过32倍、16倍、8倍下采样，所以我们输入的图片尺寸一定要为32的倍数。

3.7 Neck特征拼接部分

关于Neck详细拼接部分可以看下面这幅详细网络图，这里以256x256x3尺寸为例，最后输出的feature map分别是8x8x255、16x16x255、32x32x255。

先看第一个concat操作，我们希望将16x16x512与8x8x512的特征图拼接成16x16x255，我们对8x8x512特征图使用1x1卷积进行降维操作，减少了一半的通道数，变为了8x8x256，再进行上采样提升特征图的尺寸，变为16x16x256；再将16x16x512与16x16x256进行concat操作(concat可以理解为将两个尺寸一样，但是厚度不一样的书堆叠在一块)，通道相加变为16x16x765，再经过一系列卷积操作变为我们想要的feature map。

第二个concat是将我们第一个concat之后16x16x256与中间的32x32x256特征图进行concat，所以我们下采样8倍的feature map既有深层的特征参数，也有第一个concat的特征参数。

3.7 head输出部分

预测对象类别时不使用softmax，改成使用逻辑回归logistic的输出进行预测。这样能够支持多标签对象（比如一个人有Woman 和 Person两个标签）

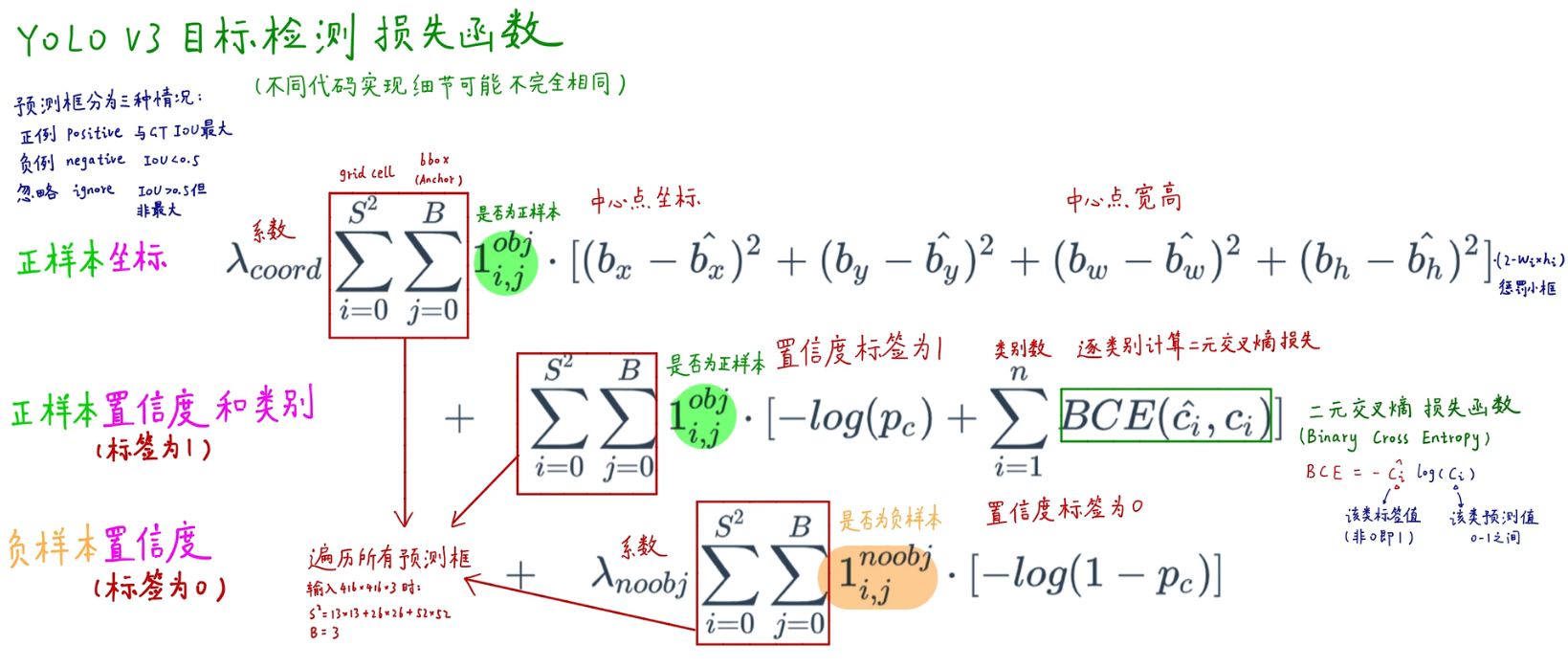
四、损失函数

正负样本
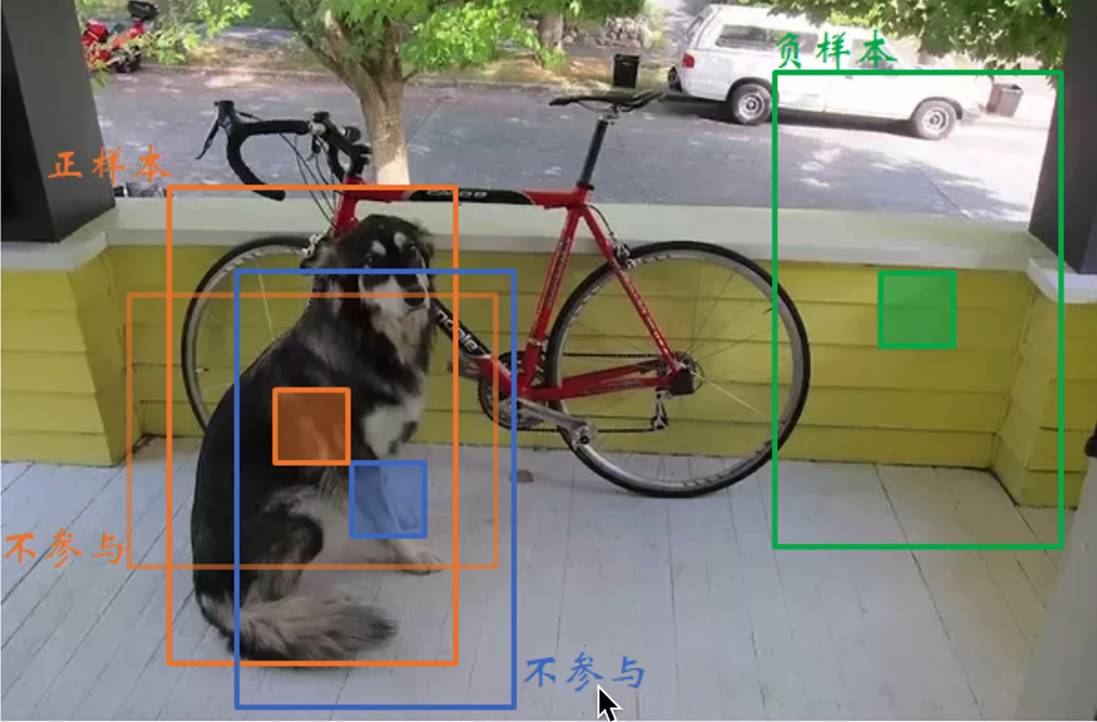
预测框可以分为三种情况：

1. 正样本：与标准框IOU最大的框
2. 不参与：与标注框IOU>0.5，但不是最大
3. 负样本：与标注框IOU<0.5

以下面这幅图为例，橙色框有两个，假设我们阈值IOU=0.5，这两个橙色框与标注框之间的IOU>0.5，我们选取最大IOU值的为正样本，另外一个橙色框不参与。

像蓝色框和绿色框与标注框之间的IOU<0.5，则为负样本。

损失函数计算公式

五、yolov3训练过程与预测过程