〔全网最正确〕2024华数杯B题成品论文22页word+四小问可执行代码+代码调式+结果分析+高清运行结果图

华数杯A题光伏发电

一、问题分析 （完整版见文末）

问题一：

首先题目要求得到电能行业与经济状况、居民消费水平、城市化率和市场化程度等因素的关系，并对供电量进行预测。其中，电能采用供电量数据、经济采用GDP数据，消费水平采用居民收入水平或消费水平数据，市场化采用中国市场化综合指标，再加上城市化率数据，进行相关性分析得到对应关系整体来看，分关系判断和预测两个部分，一是使用相关性分析、差异性分析等方法来判断因素之间的联系程度，包括皮尔逊分析、斯皮尔曼分析等。二是使用时间序列预测模型， 对供电量采用LSTM、ARIMA等模型对时间数据进行预测得到结果。但是供电量受其他因素影响，因此需要添加一定的突发性波动或是非线性规律，也可以采用BP神经网络等进行预测。

• 问题分析

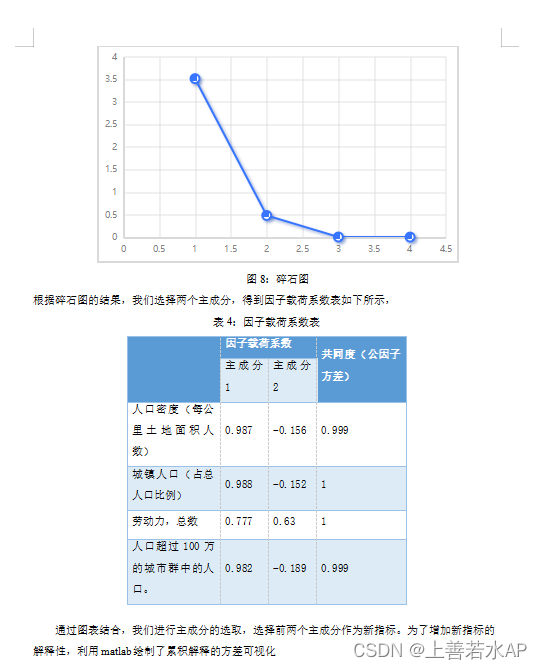
2.1 问题一分析

问题一，建立电力供应预测模型。以电力供应为关键词，在知网、PubMed、Google Scholar等期刊检索网站进行检索，查阅相关文献。对查阅的文献涉及的关键词进行频数标记，最终选择出现频率较高的指标作为本题研究电力供应的指标。最终得到经济与产业类、能源消费与结构类、人口与社会类、环境与排放类四大类指标17项指标数据。为了找到相关的数据，利用python数据爬虫以及自行寻找等方式，在国家统计局、工信部、能源局、世界银行等开放数据库获取数据。

对于数据预处理，利用收集到的数据集利用q-q图以及k-s检验判定分布方式，得出数据基本服从正态分布。对于数据进行3σ原则判定异常值。将异常值替换为缺失值，对于缺失值，这里采用牛顿线性插值的方式。由于指标数量过多，这里使用KMO检验和Bartlett球形检验判定指标独立性，对于通过检验的使用主成分分析法进行降维，对于未通过检验的指标使用相关性分析进行降维。利用降维后的数据进行相关性分析，判断指标与电力供应之间的关系。

利用数据预处理之后的数据，建立LSTM预测模型，对2024年到2060年电力供应进行预测。

2.2 问题二分析

问题二，利用羲和能源气象大数据平台收集到我国十个地区的光伏发电相关数据，对该数据集采用与问题一相同的数据清洗方式。利用数据预处理之后的结果，构建主成分分析模型，对十个地区进行评价，得出最好的地方，从而完成光伏电站选址模型构建与求解。

2.3 问题三分析

问题三，利用数据爬虫方式，收集数据。以光伏发电量最大为目标函数，引入开关变量，以及选材作为决策变量。通过分析数据，得出具体的变量之间的关系，构建等式与不等式约束条件。为了进一步提升求解速度，引入粒子群算法进行求解。关注公众号 BZD数模社 领取相关资料

2.4 问题四分析

问题四，收集碳排放相关的数据集。对数据进行预处理，使用回归预测、灰色预测、LSTM进行预测，对预测结果以误差最小为目标函数，构建优化模型进行加权。进项两次预测模型的求解，第一次将光伏发电相关的数据剔除后，进行预测。第二次，引入光伏发电相关数据进行预测。比较两种不同情况下，有无光伏发电的碳排放变化结果。从而实现对于可持续发展战略规划的分析。

综上所述，基于前四个问题的研究结果，简要概述主要发现和建议，给中国政府写一封关于光伏发电的信。

lear, clc, close all;

% 读取数据
A = readmatrix('问题4.xlsx', 'Sheet', '装机容量');
D = A(:, 8);

% 灰度预测方法
order = 2;  % 灰度预测的阶数，可以根据需要调整
numPoints = length(D);
futurePoints = 36;

% 创建预测矩阵
X = zeros(numPoints - order, order);
Y = D(order + 1:end);

% 填充预测矩阵
for i = 1:order
    X(:, i) = D(i:numPoints - order + i - 1);
end

% 进行灰度预测
coefficients = X \ Y;
predictedValues = zeros(futurePoints, 1);

for i = 1:futurePoints
    predictedValues(i) = coefficients' * D(end - order + 1:end);
    D = [D; predictedValues(i)];
end

% 计算残差
residuals = Y - X * coefficients;


predictedValues = [D(24,1),predictedValues']
predictedValues2 = 1-predictedValues
% 绘制原始数据、预测结果和残差
figure;
subplot(2,1,1);
plot(1:numPoints, A(:, 8), 'b.-', 'LineWidth', 1.5, 'MarkerSize', 12, 'DisplayName', '可再生原始数据');
hold on;
plot(numPoints :numPoints + futurePoints, predictedValues, 'r.-', 'LineWidth', 1.5, 'MarkerSize', 12, 'DisplayName', '可再生预测结果');
xlabel('数据点');
hold on;
plot(1:numPoints, A(:, 10), 'g.-', 'LineWidth', 1.5, 'MarkerSize', 12, 'DisplayName', '火电原始数据');
hold on;
plot(numPoints :numPoints + futurePoints, predictedValues2, 'k.-', 'LineWidth', 1.5, 'MarkerSize', 12, 'DisplayName', '火电预测结果');
ylabel('数值');
title('灰度预测及残差分析');
legend('show');
grid on;


subplot(2,1,2);
stem(1:length(residuals), residuals, 'b', 'LineWidth', 1.5, 'MarkerSize', 8, 'DisplayName', '残差');
xlabel('数据点');
ylabel('残差');
title('残差分析');
grid on;

点击链接加入群聊【2024华数杯数学建模】：