五分钟学完决策树ID3算法

基础概念

由于涉及到数学符号不好打字，放几张基础概念图。如果你是小白，你不要被下面的公式迷惑。这其实很简单，你看不懂可以先略过，结合后面的实例来理解这个公式，等看完实例你就懂了。不过下面关于这个公式的描述可以说非常具体了，阅读体验还是不错的。

信息熵

信息增益

---

特征选择策略

在决策树的构建过程中，选择哪个特征作为节点来分割数据是一个关键决策。这个过程通常基于以下几种策略之一：

1、信息增益（Information Gain）： 信息增益是一种常用的特征选择标准，它基于信息论的概念。在每个节点上，计算每个可用特征的信息增益，选择具有最大信息增益的特征作为节点。信息增益衡量了通过特征分割数据后，不确定性减少的程度。

2、基尼不纯度（Gini Impurity）： 基尼不纯度是另一种用于特征选择的标准。在每个节点上，计算每个可用特征的基尼不纯度，选择具有最小基尼不纯度的特征作为节点。基尼不纯度度量了从数据集中随机选择两个样本，它们不属于同一类别的概率。

3、均方差（Mean Squared Error）： 均方差通常用于回归问题中。在每个节点上，计算每个可用特征的均方差，选择使得子集中样本的均方差最小的特征作为节点。

选择哪种特征选择标准取决于具体的问题和数据特征。信息增益和基尼不纯度通常用于分类问题，而均方差通常用于回归问题。

---

本文ID3算法选择的是信息增益这个策略。

算法实例

数据集描述：在天气、温度、潮湿、有无风等特征下，是否出去玩。本文是先图后文，意思就是你先看图，图后面的文字是紧跟上面的图片的。

熵

分割线----------------------------------------------------------------------------

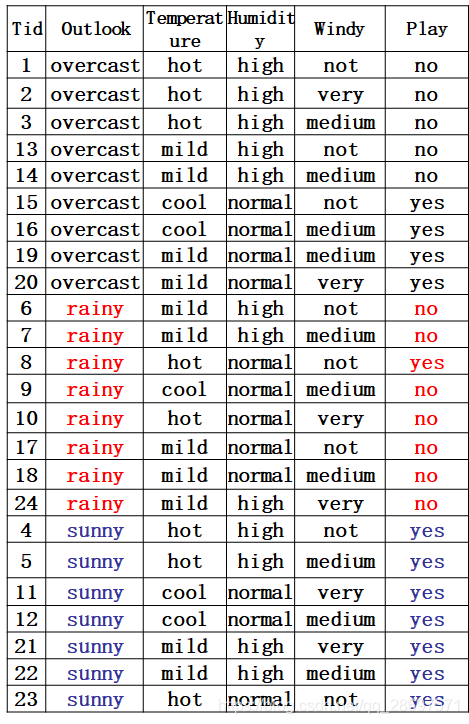
第一种因素Outlook的熵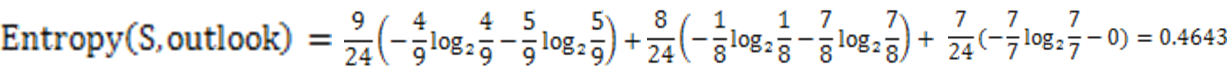

分割线----------------------------------------------------------------------------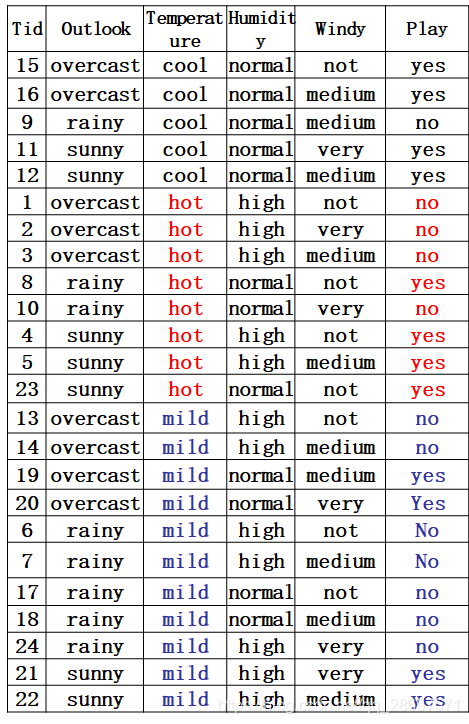

第二种因素的熵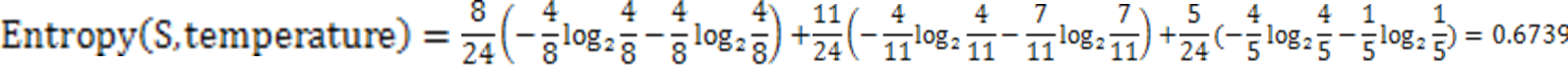

分割线----------------------------------------------------------------------------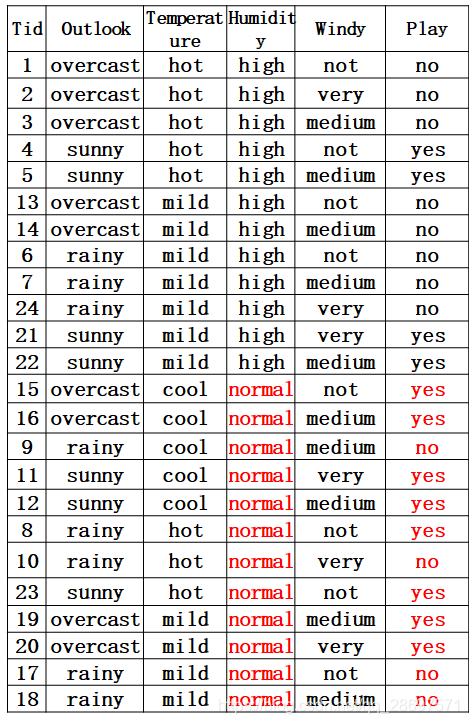

第三种因素的熵：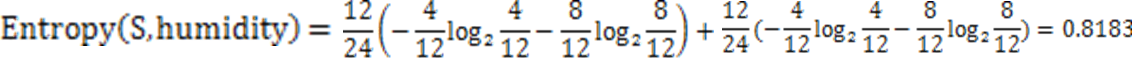

分割线----------------------------------------------------------------------------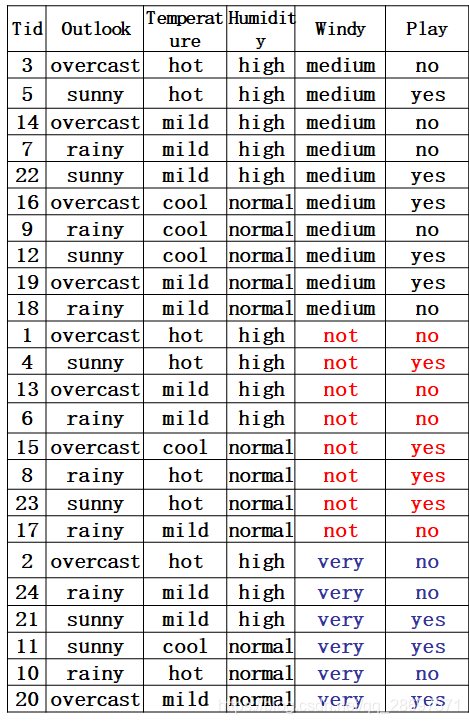

第四种因素的熵：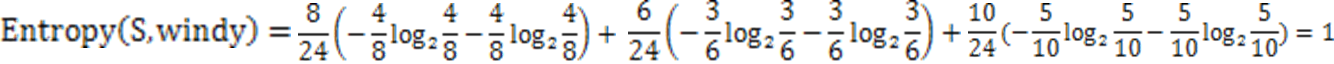

分割线----------------------------------------------------------------------------

最后选择信息增益最大的作为根节点：outlook
接着对outlook下的三种因素计算重复以上的运算：
Entropy(outlook),Entropy(outlook,overcast),Entropy(outlook,rainy),Entropy(outlook,sunny)
接着求信息增益：
发现在overcast时，humidity的信息增益最大，所以选择humidity作为叶节点。
发现在rain时，windy的信息增益最大，选择windy作为叶节点。
依次最后得到下面的结果。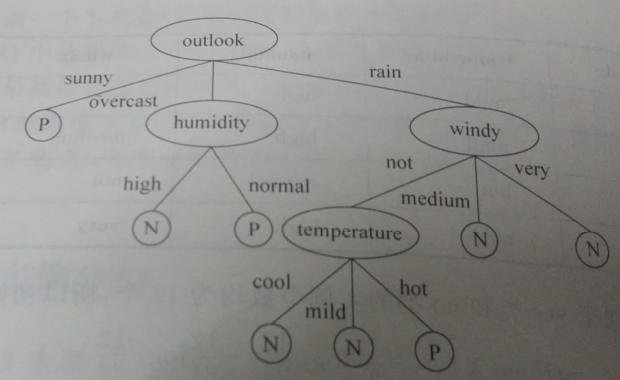

因为带log的计算手工很难算具体值，没有去检验，但是方法是没问题的