前缀和算法模板
发布时间:2024年01月14日
本系列专栏主要是整理一些常见的算法模板
方便归纳总结以及后面复习
一维前缀和
a数组为原数组,s数组为前缀和数组
前缀和数组公式 : s[i]=s[i - 1]+a[i]
求区间[l,r]和公式 : sum=s[r]-s[l-1]
"前缀和数组"和"原数组"可以合二为一
S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]
一维前缀和模板题

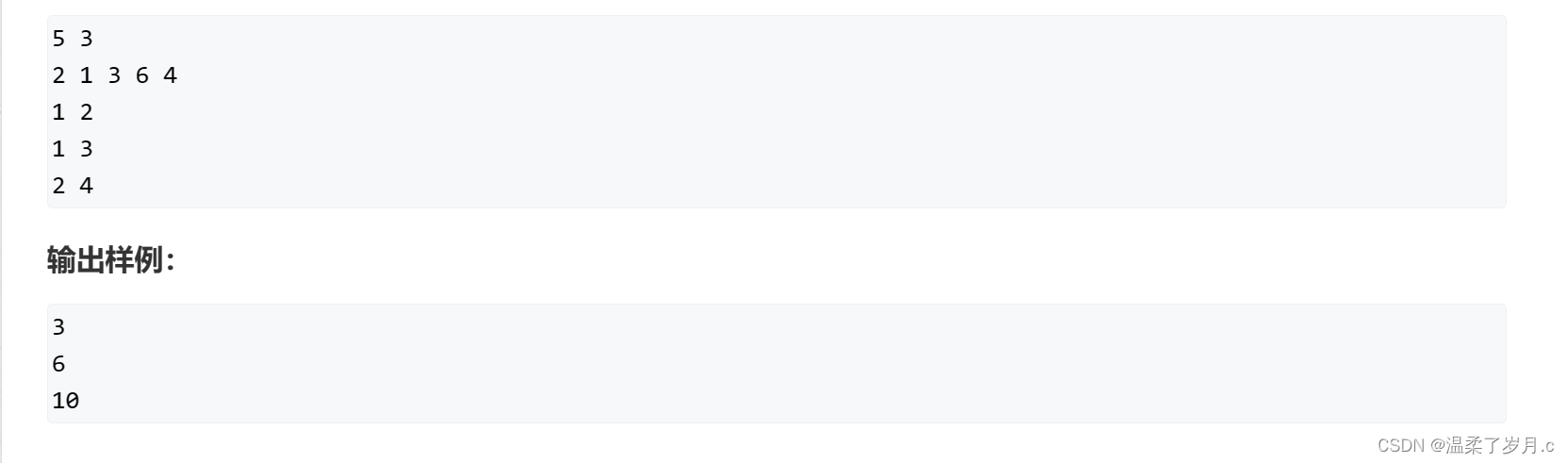
//第l个数到第r个数的和,类似相当于求等差数列的前项和
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 100001;
int arr[N]; //原数组
int S[N]; //前缀和数组
int main()
{
int m, n;
scanf("%d%d", &m, &n);
for(int i = 1; i <= m; i++)
{
scanf("%d", &arr[i]);
S[i] = S[i - 1] + arr[i];
}
while(n--)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", S[r] - S[l - 1]);
}
return 0;
}
二维前缀和
a数组为原数组,s数组为前缀和数组
S[i, j] = 第i行j列格子左上部分所有元素的和
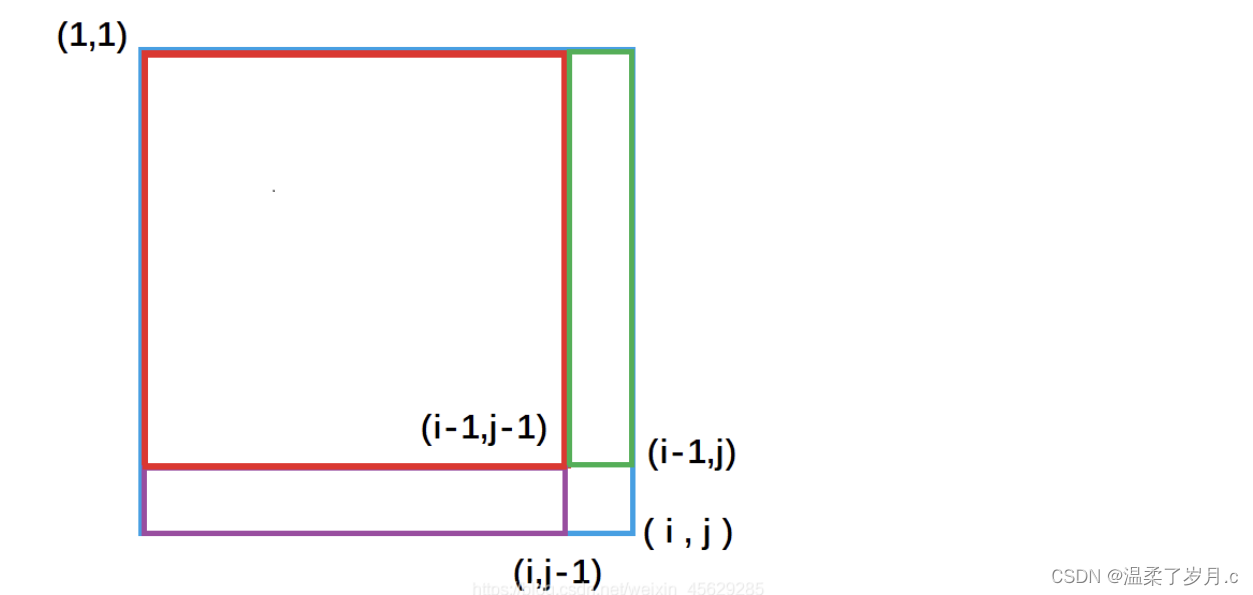
前缀和数组公式: s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]
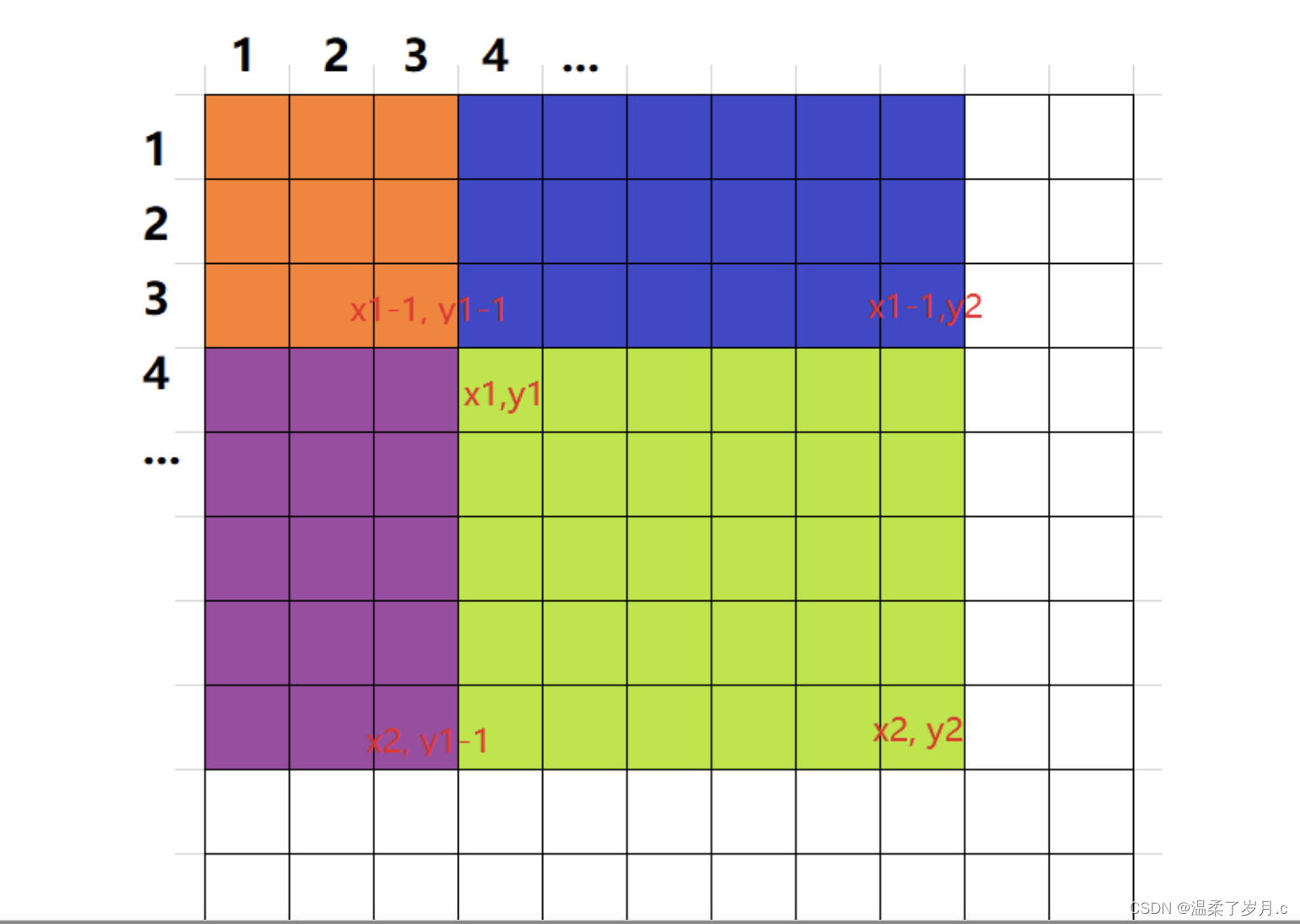
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:
S[x2][y2] - S[x2][y1 -1 ] - S[x1 - 1][y2] + S[x1- 1 ][y1 -1]
前缀和数组
前缀和数组公式: s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]
如图所示,绿色区域为前缀和区域
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和公式:
S[x2][y2] - S[x2][y1 -1 ] - S[x1 - 1][y2] + S[x1- 1 ][y1 -1]
二维前缀和模板题

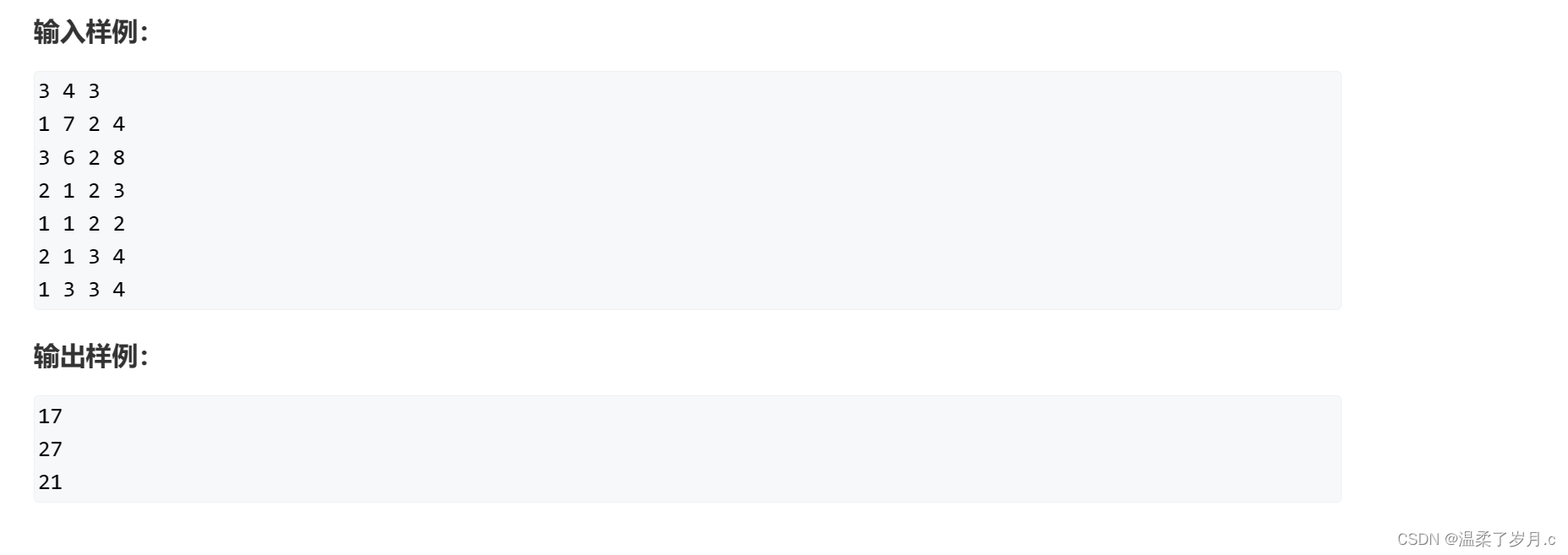
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1010;
int arr[N][N]; //原来数组
int S[N][N]; //前缀和数组
int main()
{
int n, m, q; // n行,m列,q询问
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
scanf("%d", &arr[i][j]);
S[i][j] += S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + arr[i][j]; //求前缀和
}
}
while(q--)
{
int x1, x2, y1, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", S[x2][y2] - S[x2][y1 -1 ] - S[x1 - 1][y2] + S[x1- 1 ][y1 -1]);
}
return 0;
}
文章来源:https://blog.csdn.net/m0_74228185/article/details/135586311
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 内存泄漏检测方式
- 【腾讯云中间件】2023年热门文章集锦
- 零基础学Python网络爬虫案例实战全流程详解(入门与提高篇)
- 如何查看自己的文章是否被数据库收入?【查收查引】
- 【java】7:程序控制结构
- Lua学习笔记 — Table与Metatable(超详细)
- 【文本到上下文 #2】:NLP 的数据预处理步骤
- 五、程序流程结构(1)选择结构——三目运算符
- 磁盘管理------逻辑卷、磁盘配额
- 配网故障定位:实现高效抢修的必备技能