python量化开发【中级进阶】
一、就业方向:
1、投资银行:高盛、华泰联合证券
2、证券公司:中信证券、国泰君安证券
3、私募基金:幻方量化、UBI
4、会计事务所:普华永道、Deloitte
5、软件公司:蚂蚁集团、万得
二、就业要求:
1、证券机构:金融投研及金融工程团队、一般要求硕士以上
2、私募公司:注重个人能力,学历要求并不高
3、金融科技:通用策略模型开发、量化交易系统及平台开发
三、行业收入:
1、总体收入较高,受金融行业整体薪资影响,目前金融行业整体薪资呈下降趋势,薪资较多集中在15-30K左右
四、工作岗位
1、量化开发工程师:开发和测试量化交易系统软件,实现策略代码实盘运行
五、工作内容
1、量化数据采集、清洗及挖掘
2、实时及历史策略回测系统开发
3、量化因子库开发及量化策略实现
4、量化大数据存储分析平台的设计与实现
5、行情数据服务的设计及实现
6、衍生数据服务的设计与实现
六、必备技能
1、熟悉Python中的至少一种,熟悉TCP/IP网络编程。具有 一定的软件架构能力
2、能够独立完成数据获取、数据采集、数据清洗、数据验证、挖掘特征等
3、熟练掌握金融分析理论、模型与计算工具,有了量化交易模型实操经验是加分项
4、在数学、概率统计、性能优化、算法等方面具有扎实的理论基础及实操经验
5、过硬的学历背景是高加分项
七、案例分享经验总结:
1、扎实的计算机理论基础与实践经验,需要coding能力,不需要有过多的金融专业知识,可在工作中边练边学,根据应聘的岗位内容提前准备
2、年龄不是太大问题,项目经验最为重要,平时积累人脉非常重要
3、可适当在中小型量化企业锻炼2年,积累能力,真正热爱量化交易,自学能力要求高
八、是否要转行量化开发
1、兴趣是最好的老师
2、独立coding,debug是量化交易的基础
3、需要很强的自学能力
4、能独立开发量化交易策略,具有一定实盘经验是非常大的加分项
八、逻辑推理面试题:
(一)烧绳子【分治思想】
1、质量不均的绳子烧尽需要1h,提供若干个绳子,请问如何计算出75min?
解法:
????????把第一根绳子点燃,完全燃烧用时1小时
? ? ? ? 取第二根绳子,两头对折一起点,完全燃烧用15分钟
? ? ? ? 两个时间相加则为75分钟
(二)小球称重【贪心算法,最佳情况】
1、假设你有12个外观相同的球,其中一个球和其他球的重量不一致,如果给你一个天平,最少称几次你可以找出这只球
解法:三叉树

(三)三门问题【第一次选还是第二次选的问题】
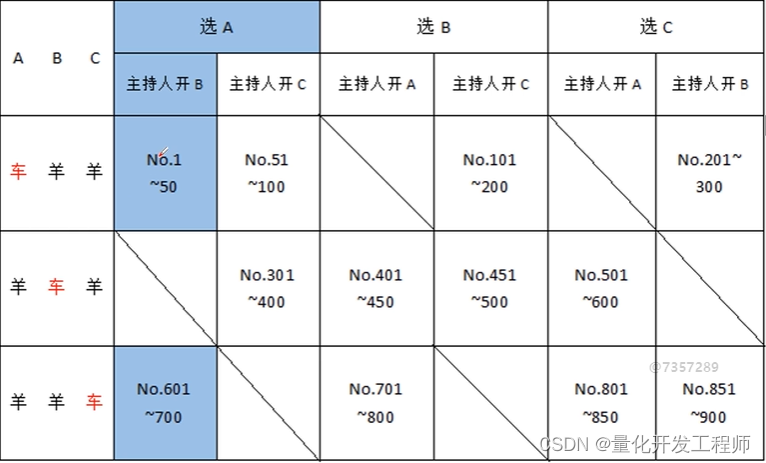
1、参赛者会看见三扇关闭了的门,选中后面有汽车的那扇门就可以赢得该汽车或奖品,而另外两扇门后面则各藏有一只山羊。你选择一扇们但不打开,这是主持人会在另两扇门中打开一个后面是山羊的门,换不换自己刚才选择的门
? ? ? ? 换,获胜概率2/3
? ? ? ? 不换,获胜概率1/3
八、概率统计类面试题:
(一)见面问题
1、两个人相约在8点到9点时间段见面,彼此等15分钟,见不到人就走。两人在8点至9点任一时刻到达目的地,求两人能见面的概率?
解法:
? ? ? ? 几何概型,总体概率空间为正方形[0,60,0,60]
? ? ? ? |x-y| <= 15
? ? ? ? 两人见面的概率 = 1 - 45*45 / 60 * 60
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? = 7/16
(二)飞机上找座位
1、有100位乘客在排队登上飞机。飞机上恰好有100个座位。每位乘客都有票,每张票对应有一个特定座位。
? ? ? ? 乘客们依次登机,A首先登上飞机,他看不懂座位号,也不知道哪个座位号是他的,所以随机选了一个座位,假装这就是他应该做的座位。
? ? ? ? 其余乘客登机依次,如果他们发现自己的座位是空的,他们会就座。如果他们发现自己的座位已经友人了,他们会随机另外选择一个座位,直到每个人都登上了飞机并就座。
? ? ? ? 那么,最后一个登上飞机的人坐在自己本来应该做的位置上的概率是多少?
解法:
? ? ? ? 考虑只有A和你的情况,你最后坐上自己座位的概率是50%
? ? ? ? 考虑只有A、B和你的情况,你最后坐上自己座位的概率是
? ? ? ? P=1/3 + 1/3 * 1/2 =50%
? ? ? ? 归纳法推理,最后一名乘客坐上自己座位的概率是50%
(三)扔硬币
1、假设我不断地扔硬币,每次扔到正面记一分,扔到反面扣一分,那么,我得到三分时,期望要扔硬多少次
思路:
? ? ? ? 设我在得0分是,扔出3分的期望次数为X0,同理可记我在得i分时,扔出3分的期望次数为Xi
? ? ? ? 得1分时,我们消耗一次机会,有1/2的概率退化为0分,有1/2的概率进化为2分,则
? ? ? ? X1=1 + 0.5X0 + 0.5X2
? ? ? ? 易得
????????X0 = 1 + X1,
????????X2= 1 + 0.5X1 + 0.5X3,
? ? ? ? X3=0
? ? ? ? 解四元一次方程得,X0=9,X1=8,X2=5,X3=0
九、编程算法类面试题:
(一)快乐数
? 1、对于一个正整数,每一次将改数替换为它每个位置上的数字的平方和。然后重复这个过程指导这个数变为1,也可能时无限循环 但始终变不到1。如果这个过程结果为1,那么这个数就是快乐数
? ? ? ? 如果n是快乐数就返回true;不是,则返回false
思路:
? ? ? ? 输入:n=19
? ? ? ? 输出:true
? ? ? ? 解释:
? ? ? ? 12+92=82
? ? ? ? 82+22=68
? ? ? ? 62+82=100
? ? ? ? 12+02+02=1
? 解法:
? ? ? ? 通过模拟替换的过程来判断一个数是否为快乐数。
? ? ? ? 如果一个数最终会变成1,那么它就是快乐数;否则,它就不是快乐数
? ? ? ? 使用一个集合来记录每次替换得到的新数,如果新数已经在集合中出现过,说明出现了循环,那么就可以退出下循环了
(二)最长回文子串
? 2、给你一个字符串s,找到s中最长的回文子串
? ? ? ? 如果字符串的反序与原始字符串相同,则该字符串称为回文字符串
?思路:
? ? ? ? 输入:s = "babad"
? ? ? ? 输出:“bab”
? ? ? ? 解释:“aba”同样是符合提议的答案
解法:
? ? ? ? 采用动态规划的方法。定位一个二维数组dp,其中dp[i][j]表示字符串从索引i到j是否为回文串
? ? ? ? 在计算dp[i][j]时,如果s[i]==s[j]且s[i+1:j-1]是回文串,那么s[i:j]也是回文串
? ? ? ? 根据上述分析,可以得到状态转移方程:dp[i][j]=(s[i]==s[j]) and dp[i+1][j-1]
? ? ? ? 在转移时,需要注意字串长度小于2的情况,即i>j-1的情况,此时dp[i][j]应该初始化为True
(三)T秒后青蛙位置
?1、给你一棵由n个顶点组成的无向树,顶点编号从1到n。青蛙从顶点1开始起跳。规则如下:
? ? ? ? 在一秒内,青蛙从它所在的当前顶点跳到另一个未访问过的顶点(如果它们直线相连)。
? ? ? ? 青蛙无法跳回已经访问过的顶点
? ? ? ? 如果青蛙可以跳到多个不同的顶点,那么它跳到任意一个顶点上的几率都相同
? ? ? ? 如果青蛙不能跳到任何未访问过的顶点上,那么它每次跳跃都会停留在原地
? ? ? ? 无向树的边用数组edges描述,其中edges[i]=[fromi,toi]意味着存在一条直线连通fromi和toi两个顶点的边,返回青蛙在t秒后位于目标顶点的target上的概率
思路:
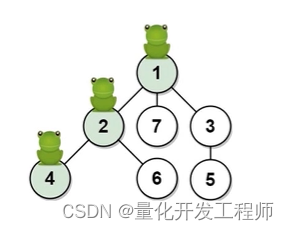
? ? ? ? 输入:n=7,edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]],t=2,target =4
? ? ? ? 输出:1/6
? ? ? ? 解释:上图显示了青蛙的跳跃路径。青蛙从顶点1起跳,第1秒有1/3的概率跳到顶点2,然后第2秒有1/2的概率跳到顶点4
? ? ? ? 因此青蛙在2秒后位于顶点4的概率是1/3*1/2=1/6
解法:
? ? ? ? 对于无向树中的任意一个点,如果它有K个未被访问的相邻节点,那么在下一秒中,青蛙有1/K的概率跳到其中任意一个节点上。如果当前节点是叶子节点 或者没有被访问的相邻节点,那么青蛙在下一秒中只能停留在原地不动
? ? ? ? 我们可以使用深度优先搜索DFS,从起点开始遍历整个无向树,在遍历过程中计算青蛙到达目标节点的概率
????????
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 网络编程套接字(Socket)
- ubuntu22上使用qemu-system-arm调试linux
- 基于web的电影院购票系统
- 大模型系列:OpenAI使用技巧_使用文本向量做语义文本搜索
- spring面试:一、面试题分类总览+bean线程安全问题+AOP相关问题(定义、使用步骤、编程式事务管理和声明式事务管理和声明式事务管理失效)
- Nextjs打包类型检查报错ype error: Property ‘card_list‘ does not exist on type(已解决)
- springboot+mysql大学生就业推荐系统-计算机毕业设计源码01535
- qt源码链接&C++automic
- 算法训练营Day43(完全背包[组合排列])
- IaC基础设施即代码:Terraform 使用 dynamic动态内联块 创建docker资源