量化交易学习笔记：XGBoost 在量化选股中的应用

一、引言

本篇文章通过借鉴传统机器学习算法——XGBoost——对相同的量价因子进行实验，方便与深度学习模型进行对比实践。

二、算法介绍

XGBoost 是在 Gradient Boosting（梯度提升）框架下实现的机器学习算法，全称为“极限梯度提升算法（eXtreme Gradient Boosting）”。

1.Boosting 算法

提升（Boosting）算法与随机森林类似，属于集成学习的一种，是一族可将弱学习器提升为强学习器的算法。先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器预测错误的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此反复，最终将T个基学习器进行加权结合。

在分类问题中，提升算法通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。提升算法的两个核心是：1.如何对前一基学习器的错误进行定义；2.如何改进本次基学习器。

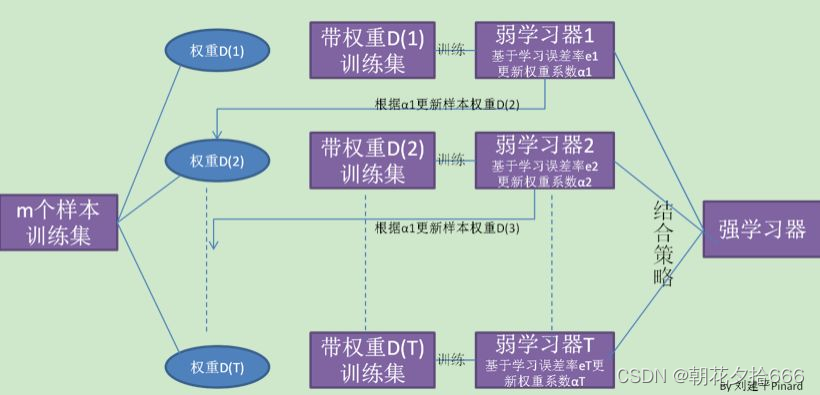
????????????????????????????????????????????????????????????????? 提升树算法

2.Adaboost 算法

AdaBoost 算法是提升算法中最具代表性的一种，其核心思想就是由分类效果较差的弱分类器逐步的强化成一个分类效果较好的强分类器。强化的过程是逐步改变样本权重，即每一次迭代时，被分类错误的样本的权重在上升，分类正确的样本的权重在下降，算法伪代码如下：

??????????????????????????????????????????????????????????????????? Adaboost 算法伪代码

上述伪代码可以理解为：

• 第1行：初始化训练数据的权值分布为等权重

• 第2行：迭代T次，即对基学习器进行T次学习提升

• 第3行：对当前迭代下的样本权重进行基学习器的训练

• 第4行：估计当前迭代下的基学习器的误差率

• 第5行：当错误率超过0.5时，跳过该基学习器

• 第6行：根据误差率计算当前基学习器的权重

• 第7行：更新下一次基学习器的样本分布

• 最后：构造所有基学习器的线性组合

在计算基学习器的误差率时，可以表示为被当前基学习器错误分类样本的权重之和：

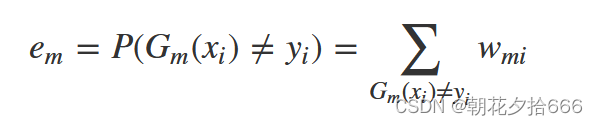
??????????????????????????????????????????????????????????? 误差率计算公式

在得到基学习器的误差率后，我们需要计算当前学习器的权重，该权重是最小化指数损失函数（exponential loss function，exp），具体公式为：

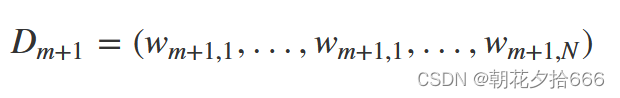
???????????????????????????????????????????????????????????????? 权重更新公式

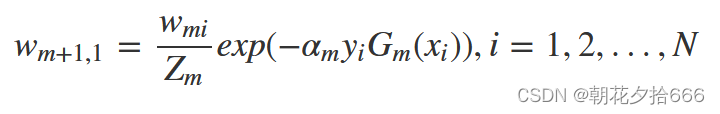
?????????????????????????????????????????????????????????????????? 最小化损失函数

这样，每一次迭代时可基于上一个基学习器的误差获取新的样本分布，并通过新的基学习器进行改进，最终通过权重将基学习器集合。

3.GBDT 算法

梯度提升树（Gradient Boosting Decision Tree）算法，是 Adaboost 算法的一个实例，决定了基学习器为决策树模型。

GBDT通过梯度下降来对新的学习器进行迭代，其中采用 CART 决策树。GBDT与Adaboost的最大区别在于：Adaboost强调自适应（adaptive），通过不断修改样本权重进行提升；而GBDT则是旨在不断减少基学习器的残差值（实际值 - 预测值），在残差减少（负梯度）的方向上建立一个新的模型。核心算法如下：

?????????????????????????????????????????????????? GBDT 算法

4.XGBoost 算法

XGBoost 可以看做是在 GBDT 上的修改，其最大的不同在于“目标函数/损失函数”的选择。不同于 GBDT 只用了一阶段形式，XGBoost 是把损失函数的二阶泰勒展开的差值作为学习目标，相当于利用牛顿法进行优化，来逼近损失函数的最小值，也就是使得损失函数为0，并在目标函数之外加入了正则项对整体求最优解。

??????????????????????????????????????????????????? XGBoost算法

XGBoost 仍然是一种提升算法，每棵树也是迭代加入的，每次迭代都希望模型效果能够提升，集成的思想如下图所示：

?????????????????????????????????????????????????????? XGBoost 集成思想

模型效果的提升主要体现在“目标函数/损失函数”下降，同时，XGBoost加入了一个 L2 正则项，该值会根据叶子结点的数量增加而增加。目标函数可以表示如下：

???????????????????????????????????????????????????????????? 损失函数

根据上文的解释，XGBoost 算法完整的目标函数可以表示为如下公式：

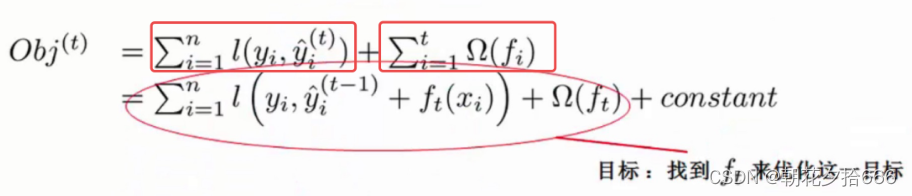
??????????????????????????????????????????????????? XGBoost 的损失函数

整体来看，XGBoost 和 GBDT 是相似的，主要区别为：

• 性质：GBDT 是机器学习算法，XGBoost 除了算法内容还包括一些工程实现方面的优化。

• 基于二阶导：GBDT 使用的是损失函数一阶导数，相当于函数空间中的梯度下降；而 XGBoost 还使用了损失函数二阶导数，相当于函数空间中的牛顿法。

• 正则化：XGBoost 显式地加入了正则项来控制模型的复杂度，能有效防止过拟合。

• 列采样：XGBoost 采用随机森林中的做法，每次节点分裂前进行列随机采样。

• 缺失值处理：XGBoost 运用稀疏感知策略处理缺失值，而 GBDT 没有设计缺失策略。

• 并行高效：XGBoost 的列块设计能有效支持并行运算，提高效率。

三、模型参数

XGBoost 算法的 pyhton API 较多，本文主要介绍模型训练的函数：

import xgboost
  
xgboost.train(params, dtrain, num_boost_round=10, *, evals=None, obj=None, feval=None, maximize=None, early_stopping_rounds=None, evals_result=None, verbose_eval=True, xgb_model=None, callbacks=None, custom_metric=None)

参数说明（parameters）

参数名	类型	默认值	可选性	解释
params	Dict[str, Any]			基学习器的参数
dtrain	DMatrix			训练数据集
num_boost_round	int			提升计算迭代次数
evals
obj	ndarray, DMatrix			自定义目标函数

基学习器的重要参数说明如下：

参数名	类型	默认值	可选性	解释
max_depth	int	6		基学习器的最大深度
max_leaves	int	0		叶节点的最大数量
learning_rate	float	0.3	range: [0,1]	学习率
objective	str	reg:squarederror	{reg:squarederror,reg:squaredlogerror,reg:logistic,binary:logistic,binary:logitraw,binary:hinge,multi:softmax}	目标函数：评估模型对于训练数据的拟合程度reg:squarederror - 平方误差reg:squaredlogerror - 均方对数reg:logistic - 逻辑回归binary:logistic - 二分类逻辑回归binary:logitraw- 二分类逻辑回归binary:hinge - 合页损失multi:softmax - 多分类
booster	str		{gbtree, gblinear, dart}	弱学习器gbtree：gblinear：dart：
tree_method	str	auto	{auto,exact,approx,hist,gpu_hist}	构建树采用的算法：即结点分裂的依据算法。不同的算法对应不同数据特征，使用效果也不相同。exact: 贪心算法approx: 近似算法hist: 分布式加权直方图gpu_hist; hist的GPU实现
n_jobs	int			并行数量
gamma	float	0		minimum loss reduction required to make a further partition on a leaf node of the tree
min_child_weight	float	1		Minimum sum of instance weight(hessian) needed in a child
max_delta_step	float	0		Maximum delta step we allow each tree’s weight estimation to be
subsample	float	1		训练样本的采样率
sampling_method	float	uniform		样本采样方法，默认为均匀采样
colsample_bytree	float	1		决定构建每一棵树的时候的采样率
colsample_bylevel	float	1		决定树的深度每增加一层时的采样率
colsample_bynode	float	1		决定每次叶节点分裂时的采样率
reg_alpha	float	0		L1 regularization term on weights (xgb’s alpha).
reg_lambda	float	1		L2 regularization term on weights (xgb’s lambda).

四、实证研究

1.因子构建

本文主要以量价数据作为原始数据计算一系列因子，基础因子包括开盘价、收盘价、最高价、成交量、换算率等行情数据，通过相关系数、标准差、时序最大、时序最小、时序求和、加权平均等统计聚合方法，构建新的因子，常用的表达式如下所示：

表达式	含义	说明
mean	时序平均	共生成7个衍生因子，例如mean(close_0，5)
ts_max	时序求最大	共生成7个衍生因子，例如ts_max(close_0，5)
ts_min	时序求最小	共生成7个衍生因子，例如ts_min(close_0，5)
std	时序标准差	共生成7个衍生因子，例如std(close_0，5)
ts_rank	时序排序	共生成7个衍生因子，例如ts_rank(close_0，5)
decay_linear	时序加权平均	共生成7个衍生因子，例如decay_linear(close_0，5)
correlation	时序相关性	生成21个个衍生因子，例如correlation(close_0，volume_0，5)
close_*	向前偏移	7*5=35个，例如close_4
衍生因子数	共计98个（7*6+21+35）

2.基准组合

在得到因子数据之后，我们随机选取一组参数构建随机森林模型，利用历史数据进行训练并根据模型预测结果构建投资组合进行回测，并将其作为我们的基准组合。具体参数如下：

• 训练数据集：2018年1月1日至2020年12月31日，全A股上市公司，上述98个量价因子数据作为特征数据，个股未来五日的收益率作为标签值。

• 测试数据集：2021年1月1日至2021年12月31日，全A股上市公司，上述98个量价因子数据作为特征数据，个股未来五日的收益率作为标签值。

• 模型参数1 基准学习器数量 / 迭代次数（num_boost_round）：30

• 模型参数2 损失函数 / 目标函数（objective）：线性回归

• 模型参数3 弱学习器类型（booster）：gbtree

• 模型参数4 树的最大深度（max_depth）：6

• 模型参数5 tree_method：approx

• 模型参数6 学习率（learning_rate）：0.3

• 模型参数7 采样率（subsample）：0.7

最后，根据训练模型对预测集数据进行预测，并利用预测结果进行选股回测。回测具体参数如下：

• 回测时间：2021年1月1日 - 2021年12月31日

• 股票池：全A股

• 手续费：买入 0.03%、卖出 0.13%

• 选股规则：模型预测打分最高前50名

• 调仓周期：5个交易日

• 单股资金最大占比：0.2

• 单股权重：得分排序加权

回测结果如下：

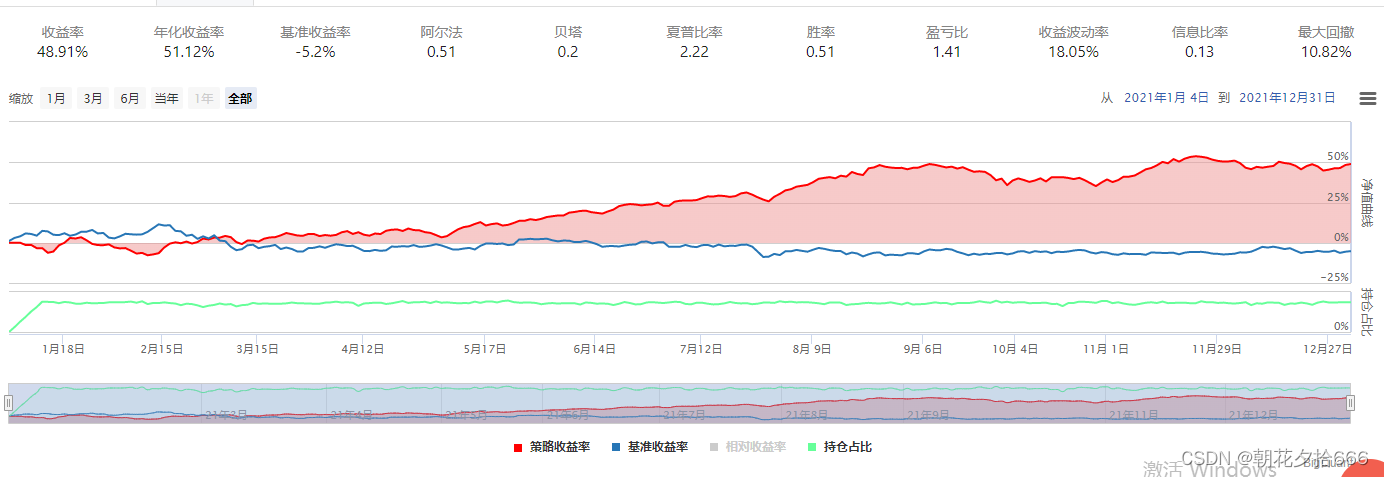
???????????????????????????????????????????????????????? 基准组合

3.对比实验

XGBoost 具有许多参数，不同的输入参数和数据集都会训练不同的模型，因此，在利用训练模型进行回测选股前，有必要对重要参数在不同输入值下的模型表现进行验证。本文选择对以下参数进行对比实验：

• 训练数据集时间周期：训练集的周期

• 基准学习器数量 / 迭代次数（num_boost_round）：迭代次数越多，模型越复杂，训练集上的准确度越高，越容易过拟合。

• 损失函数 / 目标函数（objective）：不同的数据类型和解决问题对应的目标函数不同，一般分为分类和回归两种。

• 树的最大深度（max_depth）：与迭代次数类似。

• tree_method：每个树结点分裂时的具体算法。

• 学习率（learning_rate）：梯度下降的步长。

• 采样率（subsample）：每棵树构建时所用特征的数量，为模型增加一定的随机性，防止过拟合。

选择7组输入值进行对照试验，各组模型的参数如下所示：

	基准组合	对照组1	对照组2	对照组3	对照组4	对照组5	对照组6	对照组7
迭代次数	10	50	10	10	10	10	10	10
目标函数	线性回归	线性回归	排序（pairwise）	线性回归	线性回归	线性回归	线性回归	线性回归
最大深度	6	6	6	30	6	6	6	6
tree_method	approx	approx	approx	approx	hist	approx	approx	approx
学习率	0.3	0.3	0.3	0.3	0.3	0.1	0.3	0.3
采样率	0.7	0.7	0.7	0.7	0.7	0.7	1	0.7
时间周期	2018-2020	2018-2020	2018-2020	2018-2020	2018-2020	2018-2020	2018-2020	2015-2020

回测结果汇总如下：

	基准组合	对照组1	对照组2	对照组3	对照组4	对照组5	对照组6	对照组7
年化收益率	51.12%	64.27%	57.4%	43.04%	47.7%	51.12%	49.64%	25.0%
夏普比率	2.22	2.66	2.47	2.04	2.09	2.22	2.16	1.18
最大回撤	10.82%	10.44%	9.51%	10.23%	10.94%	10.82%	9.45%	11.78%

回测结果如下所示：

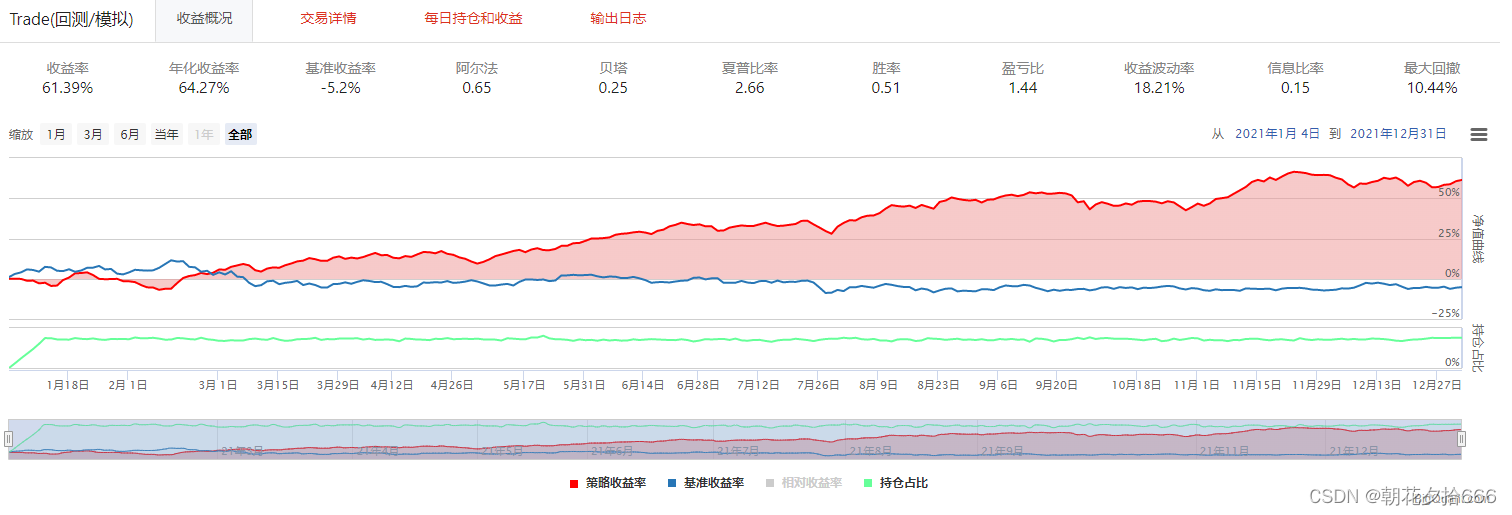
??????????????????????????????????????????????????????????????????? 对照组1

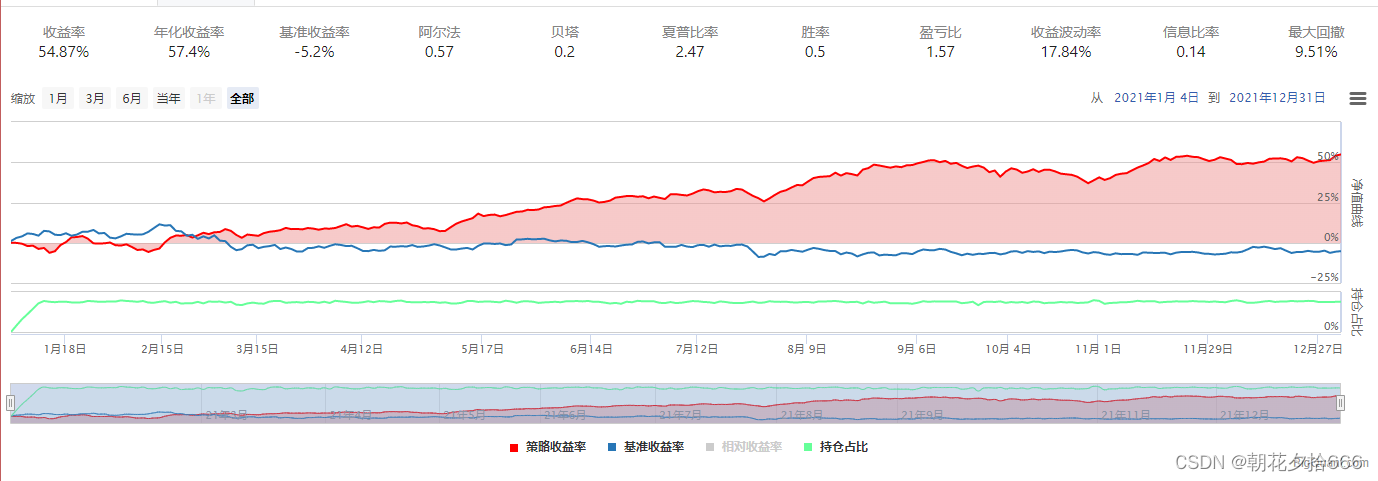
????????????????????????????????????????????????????????????????????? 对照组2

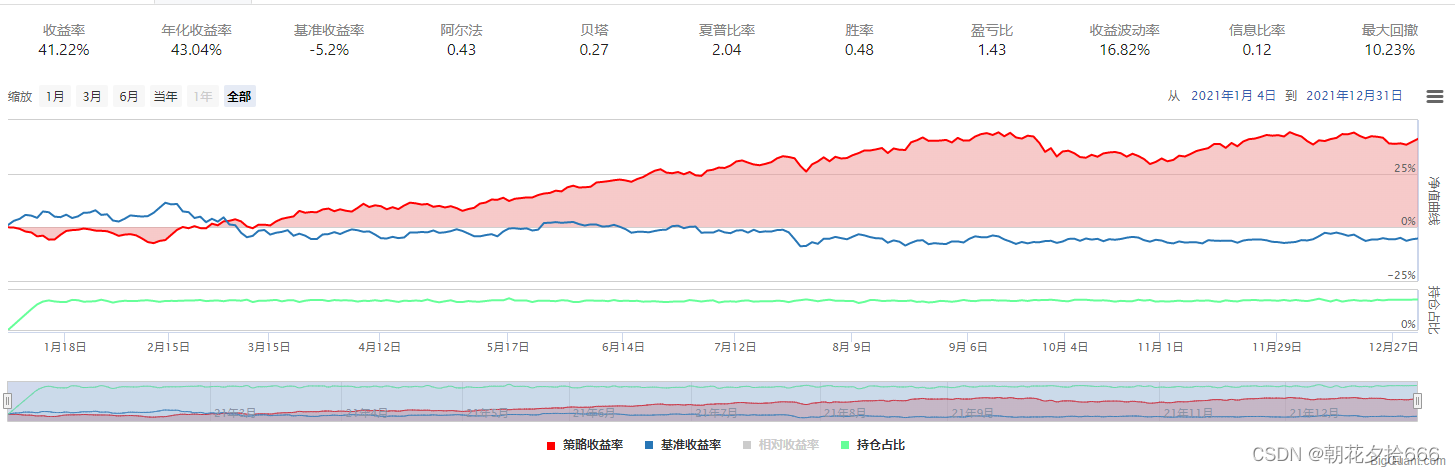
????????????????????????????????????????????????????????????????????? 对照组3

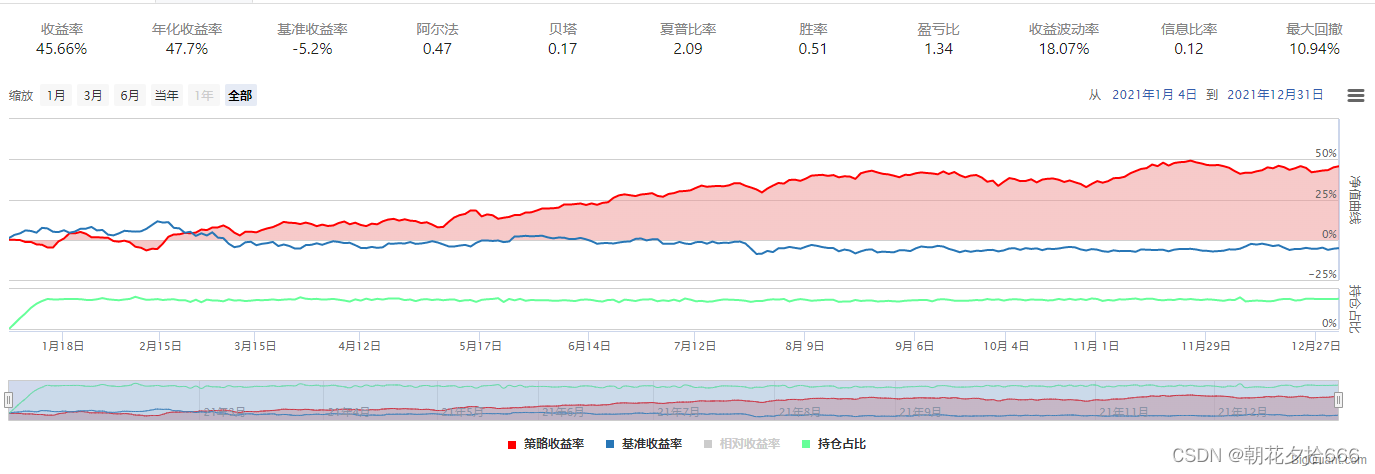
?????????????????????????????????????????????????????????????????????? 对照组4

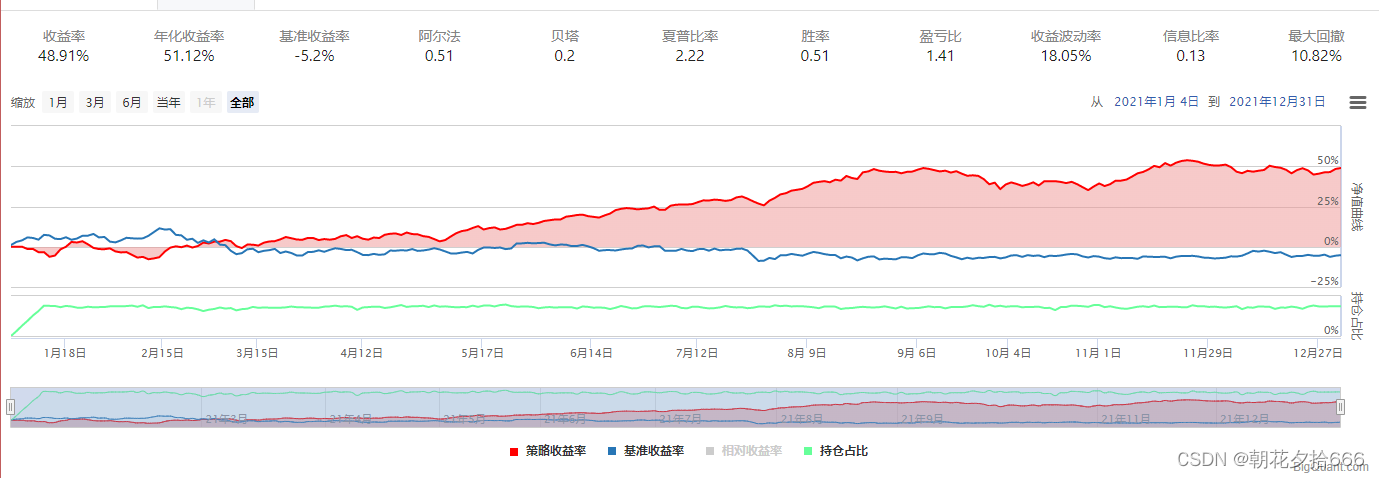
???????????????????????????????????????????????????????????????????? 对照组5

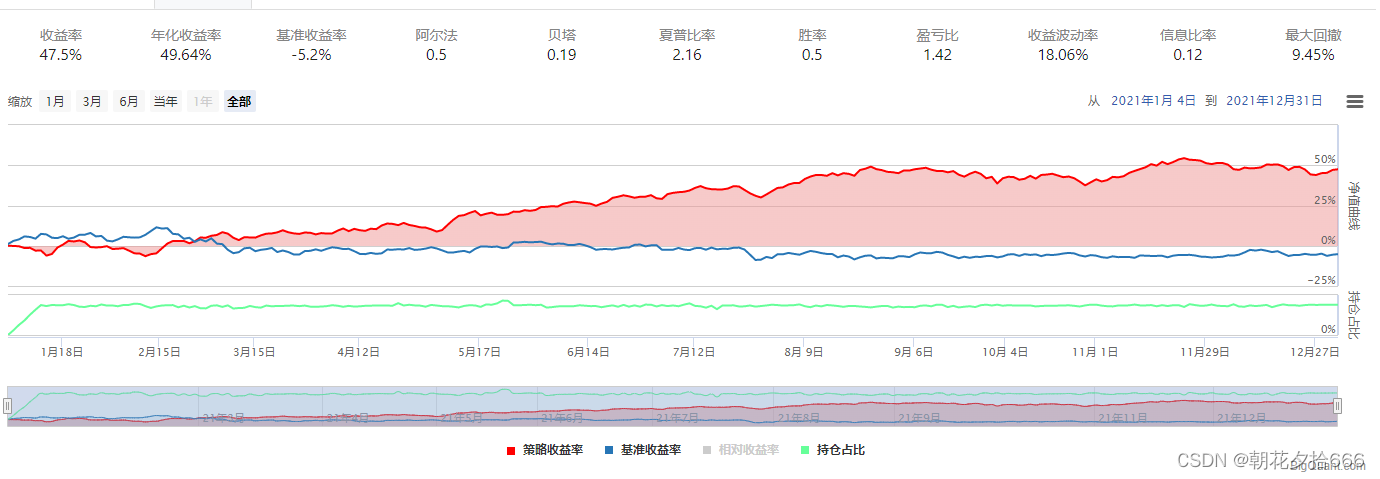
????????????????????????????????????????????????????????????????????? 对照组6

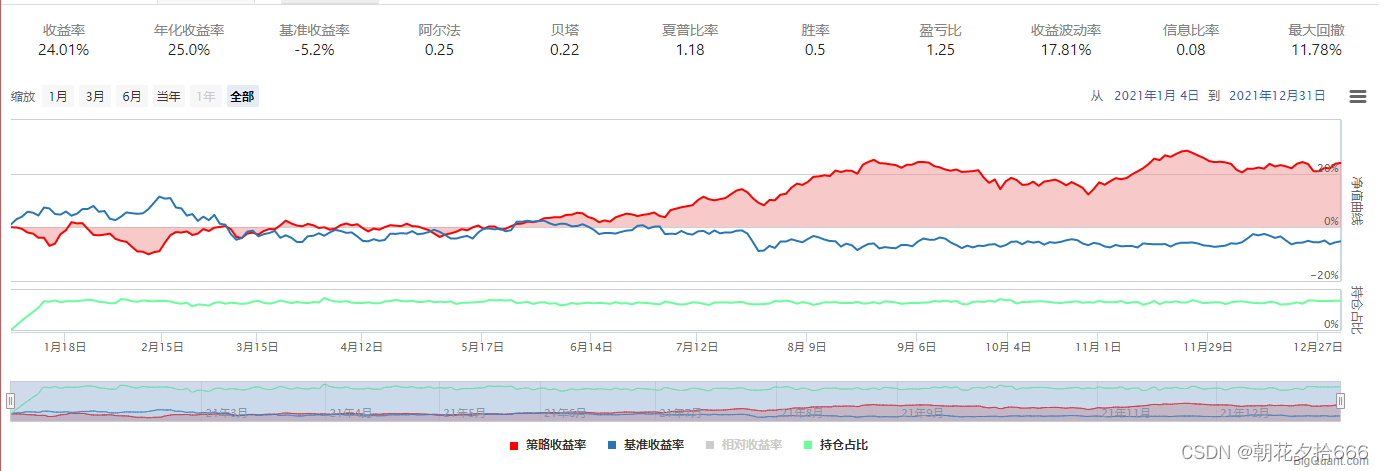
?????????????????????????????????????????????????????????????????????? 对照组7

通过对比实验，可以得到以下结论：

• 迭代次数越多，模型复杂度越高，预测准确性更好，回测效果更佳。

• approx 比 hist 的表现更好。

• 损失函数：排序（pairwise）比 线性组合 更好。

• 调整单一参数对模型影响较小。

4.参数调优

机器学习模型的参数对最终的训练结果有较大的影响，如何选择最优的一组参数训练模型是机器学习工程实践中重要的一部分。参数调优有四种方法：

• 网格搜索（GridSearch）：从预先设定好的参数集中遍历，通过交叉验证等评选效果最优的一组参数。

• 随机搜索（RandomSearch）：不同于网格搜索的暴力遍历。随机搜索从参数分布中采样，更加高效。

• 贝叶斯搜索（BayesSearch）

模型调参，第一步是要找准目标：我们要做什么？一般来说，这个目标是提升某个模型评估指标，比如对于随机森林来说，我们想要提升的是模型在未知数据上的准确率（由score或oob_score_来衡量）。找准了这个目标，我们就需要思考：模型在未知数据上的准确率受什么因素影响？在机器学习中，我们用来衡量模型在未知数据上的准确率的指标，叫做泛化误差（Genelization error）。

本文选择网格搜索的方法遍历以下参数值：

迭代次数	最大深度	学习率	结点分裂
5	5	0.01	exact
50	40	0.3	approx
			hist

网格搜索的回测结果：

	cumprod_ret	information	sharpe	sortino	max_drawdown
num_boost_round:5,max_depth:5,other_train_parameters:{tree_method:hist,learning_rat:0.01,subsample:0.7}	0.6587	0.1577	2.6352	4.5484	-0.0910
num_boost_round:5,max_depth:5,other_train_parameters:{tree_method:hist,learning_rat:0.3,subsample:0.7}	0.6587	0.1577	2.6352	4.5484	-0.0910
num_boost_round:50,max_depth:5,other_train_parameters:{tree_method:exact,learning_rat:0.01,subsample:0.7}	0.4511	0.1187	2.2565	4.0533	-0.0780
num_boost_round:50,max_depth:5,other_train_parameters:{tree_method:exact,learning_rat:0.3,subsample:0.7}	0.4511	0.1187	2.2565	4.0533	-0.0780
num_boost_round:50,max_depth:5,other_train_parameters:{tree_method:approx,learning_rat:0.01,subsample:0.7}	0.3960	0.1118	2.0110	3.5277	-0.0961
num_boost_round:50,max_depth:5,other_train_parameters:{tree_method:approx,learning_rat:0.3,subsample:0.7}	0.3960	0.1118	2.0110	3.5277	-0.0961
num_boost_round:50,max_depth:5,other_train_parameters:{tree_method:hist,learning_rat:0.01,subsample:0.7}	0.3888	0.1071	1.8873	3.3280	-0.0846
num_boost_round:50,max_depth:5,other_train_parameters:{tree_method:hist,learning_rat:0.3,subsample:0.7}	0.3888	0.1071	1.8873	3.3280	-0.0846
num_boost_round:5,max_depth:5,other_train_parameters:{tree_method:approx,learning_rat:0.01,subsample:0.7}	0.4022	0.1084	1.7979	3.1073	-0.1061
num_boost_round:5,max_depth:5,other_train_parameters:{tree_method:approx,learning_rat:0.3,subsample:0.7}	0.4022	0.1084	1.7979	3.1073	-0.1061
num_boost_round:5,max_depth:40,other_train_parameters:{tree_method:exact,learning_rat:0.01,subsample:0.7}	0.3270	0.1030	1.6076	2.6553	-0.0833
num_boost_round:5,max_depth:40,other_train_parameters:{tree_method:exact,learning_rat:0.3,subsample:0.7}	0.3270	0.1030	1.6076	2.6553	-0.0833
num_boost_round:50,max_depth:40,other_train_parameters:{tree_method:exact,learning_rat:0.01,subsample:0.7}	0.2828	0.0951	1.4594	2.4434	-0.0911
num_boost_round:50,max_depth:40,other_train_parameters:{tree_method:exact,learning_rat:0.3,subsample:0.7}	0.2828	0.0951	1.4594	2.4434	-0.0911
num_boost_round:5,max_depth:5,other_train_parameters:{tree_method:exact,learning_rat:0.01,subsample:0.7}	0.2723	0.0816	1.2457	2.1944	-0.1214
num_boost_round:5,max_depth:5,other_train_parameters:{tree_method:exact,learning_rat:0.3,subsample:0.7}	0.2723	0.0816	1.2457	2.1944	-0.1214

回测曲线如下所示：

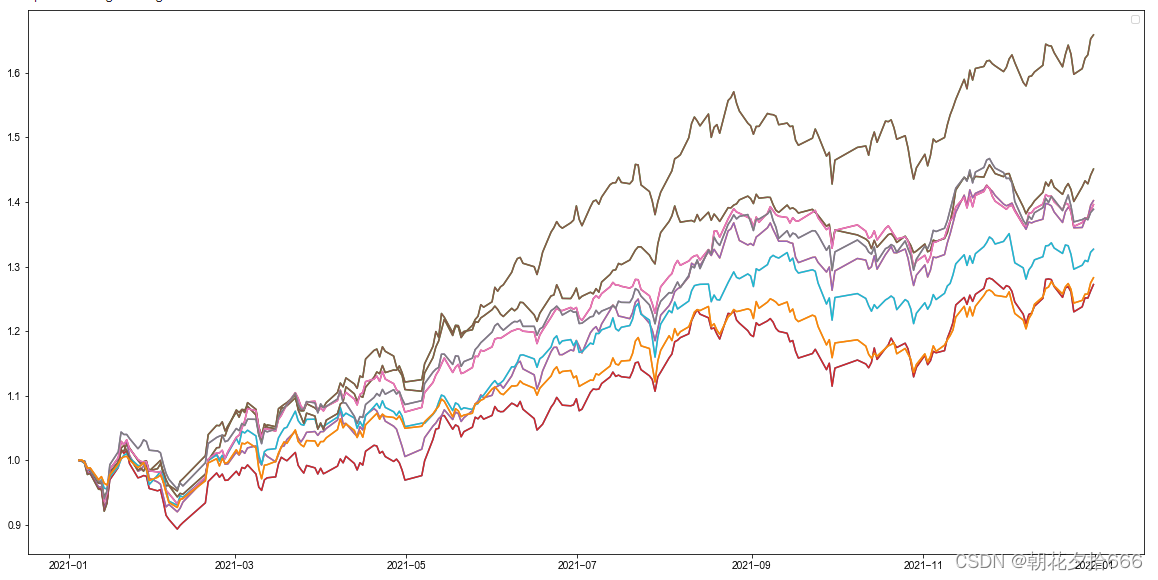
????????????????????????????????????????????????????????? 网格搜索回测曲线汇总

从网格搜索的结果来看，参数设置与前文“对比实验”的结论有所违背。由此可见，XGBoost 的参数众多，不同组合对模型影响不同，仅调整单个参数难以判断模型的优劣。

5.滚动训练

国内股票市场市场存在明显的周期性，每个周期的市场风格在不断变换，具备不同的风格特征，典型的比如2017年前的小市值风格因子。不同周期的股票池在模型训练时，其训练后的模型效果也不相同。因此，为了尽量避免策略失效，我们可以定期更新训练集数据，也就是通过滚动训练的方式更新预测模型以适应最新市场行情的变化。

本文采用2010年1月1日至2021年12月31日的数据周期，采用每年一滚动的形式，每次选取前3年的数据进行模型训练，共产生了7个数据集和7个训练模型。周期跨度如下图所示：

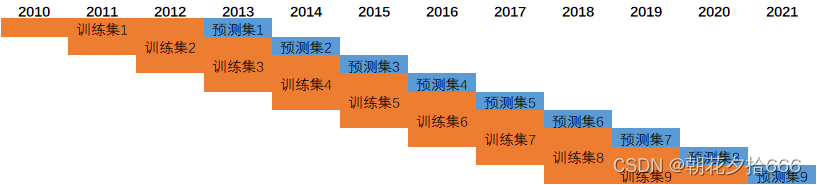
?????????????????????????????????????????????????????????????????? 滚动训练

同时，基于前文研究，我们选择以下这组参数去训练模型：

迭代次数	损失函数	模型	最大深度	结点分裂	学习率	采样率
5	线性回归	gbtree	5	hist	0.01	0.7

拟合2013年至2021年的回测曲线，如下图所示：

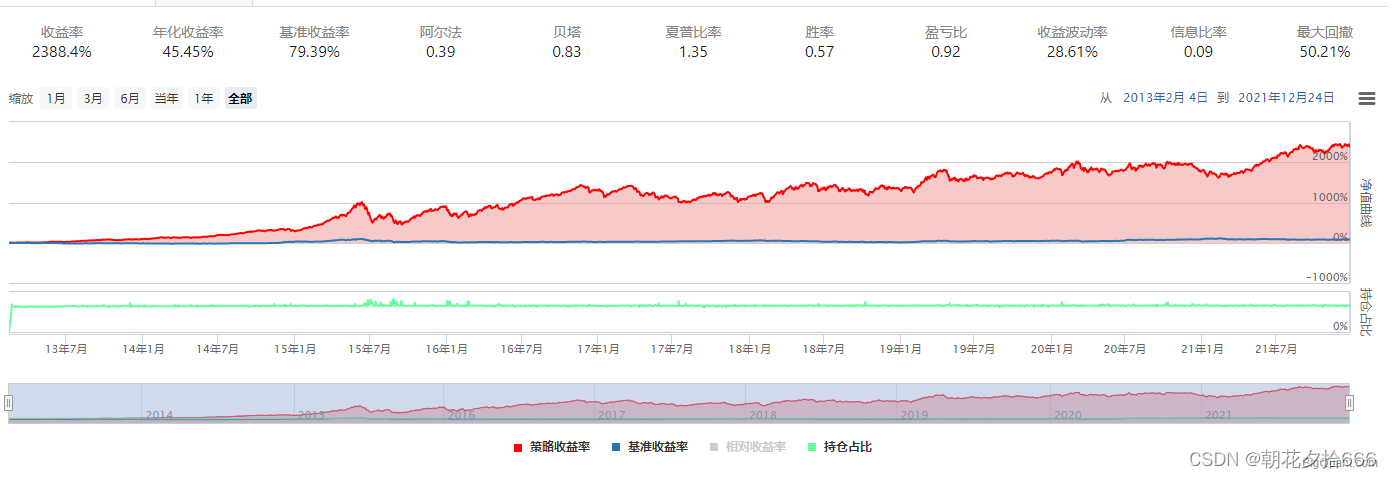
???????????????????????????????????????????????????????? 滚动训练回测曲线

滚动训练每年回测绩效表现：

年份	2013	2014	2015	2016	2017	2018	2019	2020	2021
回测表现	95.47%	100.94%	150.46%	41.29%	-10.18%	12.85%	30.73%	2.89%	31.29%

五、结论

通过上述实验，本文得到以下结论：

• XGBoost 算法在传统量价因子上具有一定的预测效果，无论是基准组合还是在对照组都具备较好的收益率表现。

• 单一参数对模型的影响不大，不同的参数组合对模型的影响不同。

• 迭代次数对模型的复杂度和准确性影响较大。

• 从滚动训练的结果来看，XGBoost算法在传统量价因子上取得较好的alpha收益，在特殊行情下仍然有较大的波动风险。

但是，上述实验仍然存在诸多不足之处，有待后续深入研究改进：

• 调参优化：正如实现结果显示，XGBoost 参数较多，工程实现难度，仅凭单一参数去调整模型难度较大，需要从训练数据类型、参数释义、问题解决等多方面入手进行调参工作。

• 数据集选择：从滚动训练结果来看，选择不同时间周期的训练集数据和预测集数据对模型训练和评估有不同的效果。

• 因子特征选择和理解：本文选择了传统量价因子作为特征集，后续可以选择更加多元化的因子集合，比如财务因子、估值因子、宏观因子、基本面因子等。同时，对于因子和标签需要进一步深入的理解和实验，比如标签除了5日收益率外，其他类型的收益率是否有显著不同。