数据结构学习 jz29 顺时针打印矩阵

关键词：模拟

题目：螺旋遍历二维数组

简单题做了超过40分钟 调了很久 不好?

方法一：

我自己做的。

思路：

xy_t：

记录xy的方向，往右走，往下走，往左走，往上走

t控制方向

std::vector<std::vector<int>>xy_t{ {0,1},{1,0},{0,-1},{-1,0} };

isx：

????????true：轮到x方向动

? ? ? ? false：轮到y方向动

bool isx = false;

n_res m_res:

? ? ? ? n_res：还没走过的行数（x方向）

????????m_res：还没走过的列数（y方向）

int n_res = n, m_res = m;

res：

? ? ? ? 现在走的方向剩余的行数/列数。

int res = isx ? n_res : m_res;

step：

? ? ? ? 现在走的这一行/这一列已经走过的步数。

记录结果，步数加一：

result.push_back(array[x][y]);
step++;

如果step+1超过res，意味着这一行/这一列走到底了：

? ? ? ? 1、如果isx==true（在x方向上走了一列），那么m_res-1?

? ? ? ? 2、如果isx==false（在y方向上走了一行），那么n_res-1?

? ? ? ? 3、isx方向反转

? ? ? ? 4、改变t控制的方向

? ? ? ? 5、step归零

            if (step + 1 > res)
            {
                n_res = isx ? n_res : n_res - 1;
                m_res = !isx ? m_res : m_res - 1;
                isx = !isx;
                t = (t + 1) % 4;
                step = 0;
            }

走下一步：

            x = x + xy_t[t][0];
            y = y + xy_t[t][1];

?比如：

先沿y方向走一行。

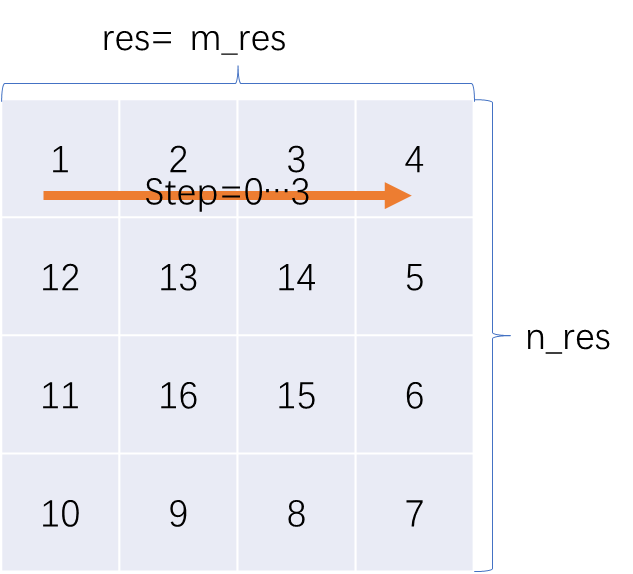
走完之后，n_res--

再沿x方向走一列。

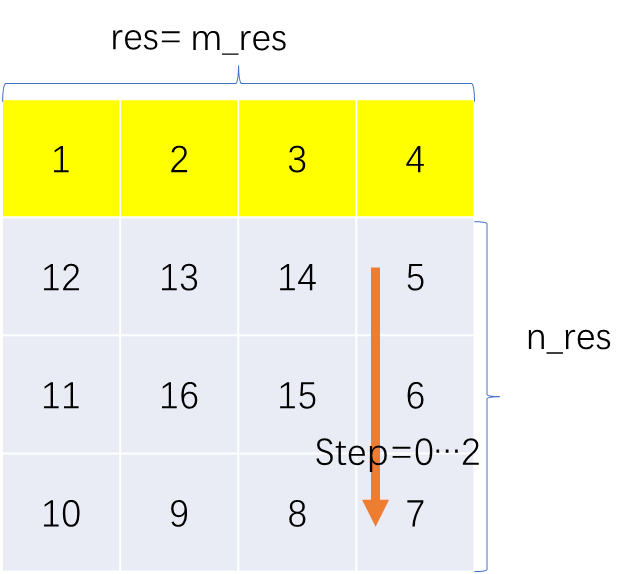
走完之后，m_res--

循环这个过程直到所有数被走完。

复杂度计算：

时间复杂度O(nm)

空间复杂度O(1)

代码：

class Solution {
public:
    std::vector<int> spiralArray(std::vector<std::vector<int>>& array) {
        std::vector<int> result;
        if (array.empty() || array[0].empty()) return result;
        int n = array.size(), m = array[0].size();
        int x = 0, y = 0;
        std::vector<std::vector<int>>xy_t{ {0,1},{1,0},{0,-1},{-1,0} };
        bool isx = false;
        int n_res = n, m_res = m;
        int step = 0;
        int t = 0;
        for (int i = 0; i < n * m; i++)
        {
            int res = isx ? n_res : m_res;
            result.push_back(array[x][y]);
            step++;
            if (step + 1 > res)
            {
                n_res = isx ? n_res : n_res - 1;
                m_res = !isx ? m_res : m_res - 1;
                isx = !isx;
                t = (t + 1) % 4;
                step = 0;
            }
            x = x + xy_t[t][0];
            y = y + xy_t[t][1];
        }
        return result;
    }
};

方法二：

看了k神的提示，弄了四面会活动的墙。显然比我原本的好。

思路：

四面墙：

? ? ? ? l左墙

? ? ? ? r右墙

? ? ? ? t上墙

? ? ? ? b下墙

int l = 0, r = m - 1, t = 0, b = n - 1;

cut：

? ? ? ? 统计已经走过的格子的个数。

从左往右走：

碰到右墙就停止。

走完之后上面第一行已经走完，上墙往下移动一行，t++。

            for (int i = l; i <= r; ++i)
            {
                cut++;
                result.push_back(array[t][i]);
            }
            if (cut >= m * n) break;
            t++;

从上往下走：

碰到下墙就停止。

走完之后右边第一列已经走完，右墙往左移动一列，r--。

            for (int i = t; i <= b; ++i)
            {
                cut++;
                result.push_back(array[i][r]);
            }
            if (cut >= m * n) break;
            r--;

从右往左走：

碰到左墙就停止。

走完之后下面第一行已经走完，下墙往上移动一行，b--。

            for (int i = r; i >= l; --i)
            {
                cut++;
                result.push_back(array[b][i]);
            }
            if (cut >= m * n) break;
            b--;

从下往上走：

碰到上墙就停止。

走完之后左边第一列已经走完，左墙往右移动一列，l++。

            for (int i = b; i >= t; --i)
            {
                cut++;
                result.push_back(array[i][l]);
            }
            if (cut >= m * n) break;
            l++;

复杂度计算：

时间复杂度O(nm)

空间复杂度O(1)

代码：

class Solution {
public:
    std::vector<int> spiralArray(std::vector<std::vector<int>>& array) {
        std::vector<int> result;
        if (array.empty() || array[0].empty()) return result;
        int n = array.size(), m = array[0].size();
        int l = 0, r = m - 1, t = 0, b = n - 1;
        int cut = 0;//统计已经放进result的个数
        while (true)
        {
            for (int i = l; i <= r; ++i)
            {
                cut++;
                result.push_back(array[t][i]);
            }
            if (cut >= m * n) break;
            t++;
            for (int i = t; i <= b; ++i)
            {
                cut++;
                result.push_back(array[i][r]);
            }
            if (cut >= m * n) break;
            r--;
            for (int i = r; i >= l; --i)
            {
                cut++;
                result.push_back(array[b][i]);
            }
            if (cut >= m * n) break;
            b--;
            for (int i = b; i >= t; --i)
            {
                cut++;
                result.push_back(array[i][l]);
            }
            if (cut >= m * n) break;
            l++;

        }

        return result;
    }
};