【Matlab】ELM极限学习机时序预测算法
发布时间:2023年12月30日
?资源下载:?https://download.csdn.net/download/vvoennvv/88681649
一,概述
? ? ? ? ELM(Extreme Learning Machine)是一种单层前馈神经网络结构,与传统神经网络不同的是,ELM的隐层神经元权重以及偏置都是随机产生的,并且在网络训练过程中不会更新。这种随机初始化的方法使得ELM的训练速度非常快,同时避免了传统神经网络中需要反复调整权重的问题。 ELM的训练过程可以概括为以下几步:
- 随机初始化隐层神经元的权重和偏置,构建网络结构。
- 将训练数据输入到网络中,得到隐层神经元的输出。
- 对隐层神经元的输出和训练数据的标签进行线性回归,得到输出层的权重。
- 在测试阶段,将输入数据输入到网络中,通过隐层神经元和输出层权重计算输出结果。 ELM 的优点在于它的训练速度非常快,同时具有较好的泛化能力和适用于大规模数据的特点。但是,它的缺点在于随机初始化可能会导致结果不稳定,而且网络结构过于简单,可能无法处理复杂的非线性问题。因此,在实际应用中需要根据具体问题进行权衡选择。
二,代码
代码中文注释非常清晰,按照示例数据修改格式,替换数据集即可运行,数据集为excel。
部分代码示例如下:
%% 清空环境变量
warning off % 关闭报警信息
close all % 关闭开启的图窗
clear % 清空变量
clc % 清空命令行
%% 导入数据(时间序列的单列数据)
result = xlsread('数据集.xlsx');
%% 数据分析
num_samples = length(result); % 样本个数
kim = 15; % 延时步长(kim个历史数据作为自变量)
zim = 1; % 跨zim个时间点进行预测
%% 构造数据集
for i = 1: num_samples - kim - zim + 1
res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];
end
%% 划分训练集和测试集
%temp = 1: 1: 922;
%P_train = res(temp(1: 700), 1: 15)';
%T_train = res(temp(1: 700), 16)';
%M = size(P_train, 2);
%P_test = res(temp(701: end), 1: 15)';
%T_test = res(temp(701: end), 16)';
%N = size(P_test, 2);
%% 数据集分析
outdim = 1; % 最后一列为输出
num_size = 0.7; % 训练集占数据集比例
num_train_s = round(num_size * num_samples); % 训练集样本个数
f_ = size(res, 2) - outdim; % 输入特征维度
%% 划分训练集和测试集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);
P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);
%% 数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);
[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);
%% 创建模型
num_hiddens = 20; % 隐藏层节点个数
activate_model = 'sig'; % 激活函数
......三,运行结果

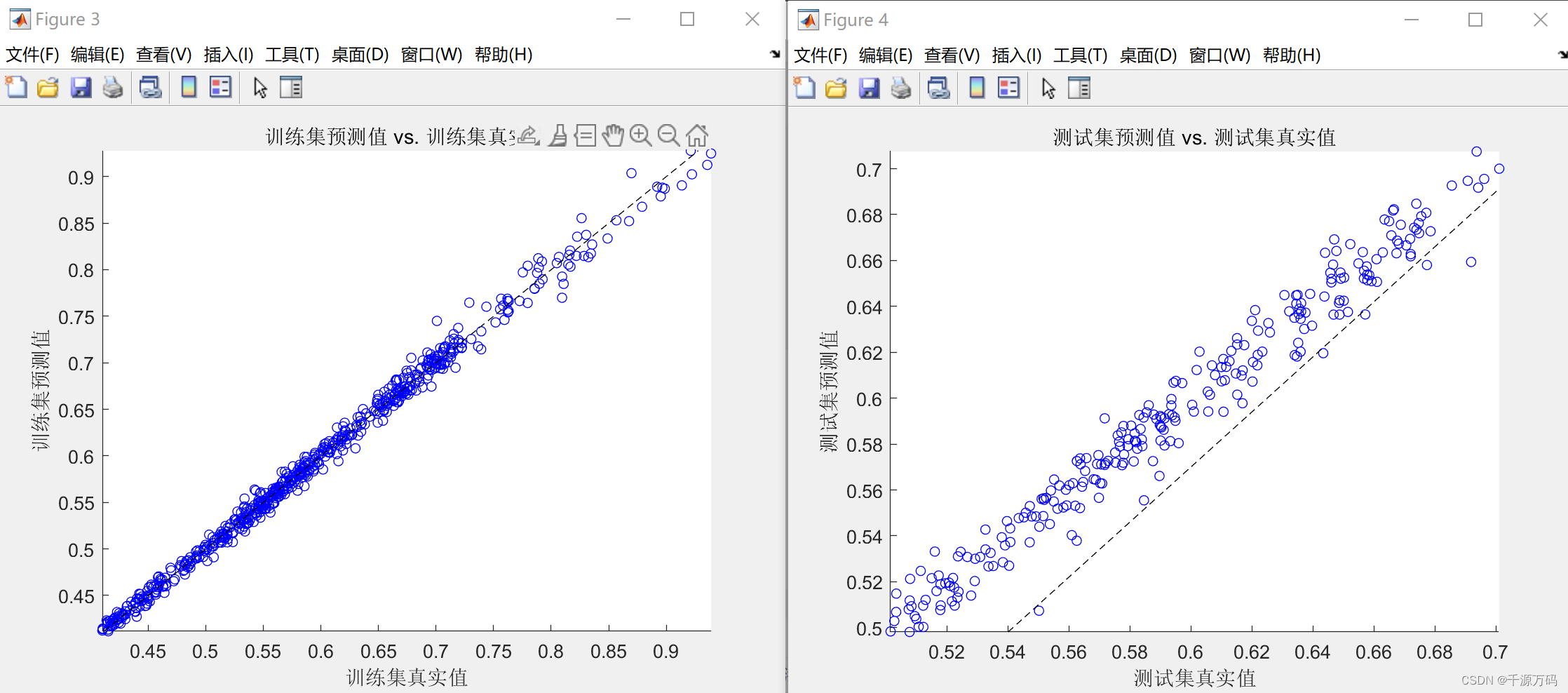
文章来源:https://blog.csdn.net/vvoennvv/article/details/135307708
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!