全网最全—差异性分析方法汇总与pk

在数据研究中，常见的数据关系可以分为四类，分析是相关关系，因果关系、差异关系以及其它。本次所进行研究的关系为差异关系。对于差异性分析方法常见可以分为三类：参数检验、非参数检验以及可视化图形。

一、参数检验

1、参数检验的选择

一般差异分析方法常见的参数检验方法一般有方差分析和t检验，对于方差分析是一个大类，t检验也是，对于这些参数检验的大体选择：

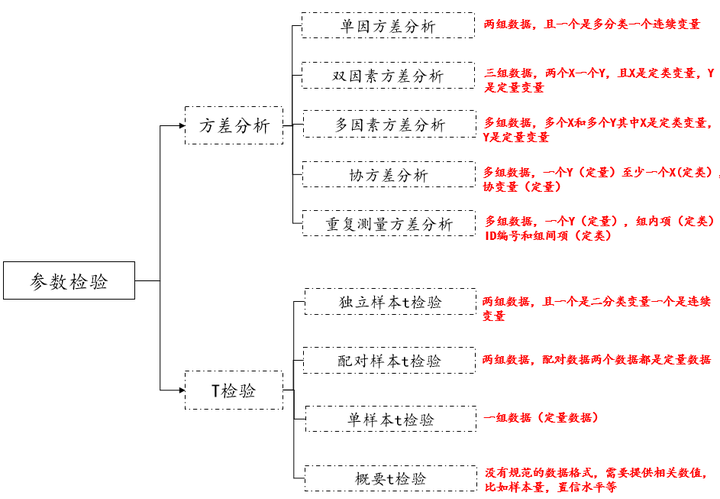
一般常见的分为方差分析和t检验，如果按照数据类型和数据格式进行选择，可以汇总如上图。以下分别进行说明方差分析和t检验。

2、方差分析

01、单因素方差分析

单因素方差说明
研究一个自变量（定类变量）与一个因变量（定量变量）之间的差异性，比如想要研究学历对产品满意度的影响、不同组（ABC三组）小鼠生存时间的差异性等。
单因素方差数据格式
单因素方差分析的数据格式共有两列一列为组别，一列为对应的分析项，一般格式如下：

比如如上格式中，1代表专科，2代表本科，3代表硕士，不同学历对产品满意度（1代表非常不满意2代表比较不满意3代表满意4代表比较满意5代表很满意）的差异性。
单因素方差操作
【通用方法：方差分析】→【拖拽分析项】→点击开始分析；

单因素方差分析结果一般格式

一般结果中会提供均值标准差以及F统计量和p值等。

02、双因素方差分析

双因素方差说明
双因素方差分析是研究两个自变量（定类变量）对因变量的差异性，比如研究学历、性别对产品满意度的差异等。
双因素方差数据格式
双因素方差分析的数据格式共有三列两列为X（定类数据），一列为对应的分析项，一般格式如下：

比如如上格式中，组别1中1代表男2代表女，组别2中1代表不锻炼，2代表偶尔锻炼，3代表经常锻炼，对应的分析项是每个样本的身高。想要研究不同性别和不同体育锻炼情况的差异性。
双因素方差操作
【进阶方法：双因素方差】→【拖拽分析项】→点击开始分析；

双因素方差分析结果一般格式

一般结果中会提供平方和，df，均方以及F统计量和p值等。除此之外，研究者还可以进行分析二阶效应，简单效应以及效应量计算等等。其分析的一般路径为：

03、多因素方差分析

多因素方差分析的分析路径以及数据格式等和双因素方差分析类似。

04、协方差分析

协方差说明
进行方差分析加入协变量，将可能干扰的变量纳入到考虑范畴中，比如说不同的工作年限对薪资是否有显著性差异，但是如果个人的学历不同也会影响薪资，这时就需要排除学历的影响等。
协方差数据格式

1个X占用1列，1个Y也占用1列，如果有协变量那么1个协变量占用1列。
协方差操作
【进阶方法：协方差】→【拖拽分析项】→点击开始分析；

协方差分析结果一般格式

一般结果中会提供平方和，df，均方以及F统计量和p值等。除此之外，研究者还可以进行分析事后多重比较、平行性检验或者进行效应量计算等等。

05、重复测量方差分析

重复测量方差说明
重复测量方差是指同一批样本对象在不同时间点上的多次测量，然后通过研究者搜集数据进行分析该指标在不同时段的变化规律。比如将手术要求基本相同的15名患者随机分3组，手术过程中分别采用A、B、C三种麻醉诱导方法，在T0（诱导前）、T1、T2、T3、T4五个时相测量患者的收缩压对比差异性。
重复测量方差数据格式
重复测量方差数据的特殊之处在于需要有ID号，比如病例号等，以及时间点数据，同一个ID（病例）会有多个不同时间点的数据，比如5个样本分别有3个相同测量时间点，一个样本有3个，那么就有5*3=15行数据。举例如下：

重复测量方差操作
【实验/医学研究：重复测量方差】→【拖拽分析项】→点击开始分析；

重复测量方差结果一般格式
重复测量方差一般会提供四个表格（spssau）：

部分格式如下：

3、T检验

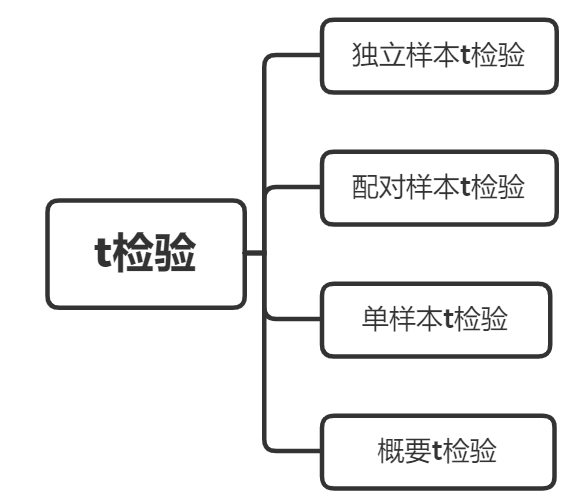
01、独立样本t检验

独立样本t检验说明
独立样本t检验一般是研究定类变量和定类变量之间的差异性，并且定类变量为二分类变量，比如研究性别和身高之间是否有显著性差异，性别包括男和女。
独立样本t检验数据格式
在进行数据分析之前都需要将数据整理成正确的数据格式然后在进行分析，那么t检验（严格讲为独立样本t检验）的数据格式是什么样的呢？如下说明：

组别为一列，分析项为一列。
独立样本t检验操作
【通用方法：t检验】→【拖拽分析项】→点击开始分析；

独立样本t检验结果一般格式

一般结果中会提供均值标准差以及t统计量和p值等。

02、配对样本t检验

配对样本t检验说明
配对的定量数据之间的差异，比如研究补习前后的学生成绩的差异，有无广告的用户的购买意愿等。
配对样本t检验数据格式
配对样本t检验的数据格式为两列，一个分析项为一列，比如下方的有无广告的用户的购买意愿，有广告的购买意愿为一列，没有广告的购买意愿为一列。

配对样本t检验操作
【通用方法：配对t检验】→【拖拽分析项】→点击开始分析；

配对样本t检验结果一般格式

分析结果一般包括配对的均值和标准差、统计量t值以及p值。

03、单样本t检验

单样本t检验说明
研究一列数据（定量数据）与某个数字之间的差异性，比如说研究某市青少年的平均身高与150cm的差异等。
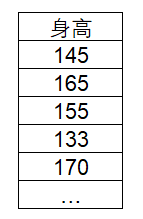
单样本t检验数据格式
单样本t检验的数据格式为一列，一般如下：

单样本t检验操作
【通用方法：单样本t检验】→【拖拽分析项】→点击开始分析；

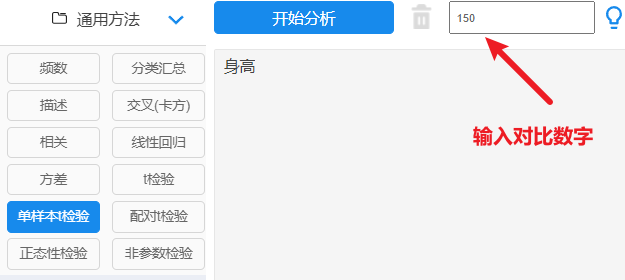
单样本t检验结果一般格式

单样本t检验有提供样本量，最小值，最大值以及t值，p值等。

04、概要t检验

概要t检验说明
想要进行t检验如果只有汇总好的统计数据（包括平均值，标准差和样本量），此时可使用概要t 检验进行分析。
概要t检验数据格式
概要t检验的数据格式与传统的t检验数据格式不同，一般在分析框内只需要输入平均值、标准差、样本量、对比均值、置信水平以及假设检验即可。

概要t检验操作
【实验/医学研究：概要t检验】→【拖拽分析项】→点击开始分析；

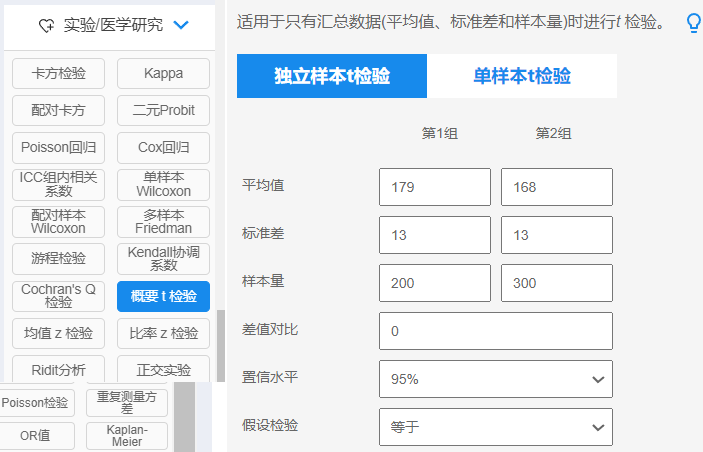
概要t检验结果一般格式
会提供假设检验和置信区间等等。

二、非参数检验

1、非参数检验的选择

对于非参数检验的差异分析方法，大体可以分为两大类一个是卡方检验一个秩和检验。对于卡方检验和秩和检验如何选择，可以参考如图：

接下来对于卡方检验和秩和检验进行一一说明。

2、卡方检验

01、Pearson卡方检验

Pearson卡方检验说明

Pearson卡方检验进行研究两组数据的差异，并且其数据分别为定类变量和定类变量，比如想要研究性别和是否吸烟之间的差异，南方和北方饮食习惯（米和面）的差异等。

Pearson卡方检验数据格式

Pearson卡方检验的数据格式为一个分析项为一列，比如下表中，性别（1代表男，2代表女）为一列，是否吸烟（1不吸烟，2吸烟）为一列，如下：

Pearson卡方检验操作

【实验/医学研究：卡方检验】→【拖拽分析项】→点击开始分析；

Pearson卡方检验结果一般格式

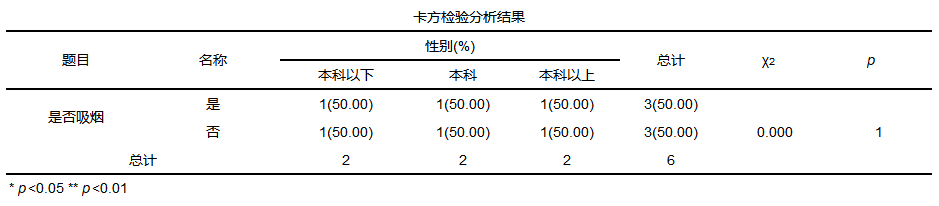
一般结果中会提供均值标准差以及卡方值和p值等。

02、Fisher卡方

fisher卡方检验说明

fisher卡方与pearson卡方类似，研究定类数据和定类数据的差异性。其与pearson卡方检验的区别是如果分析样本量较少（比如小于40），也或者期望频数出现小于5时，或者R*C结构时，也或者为汇总表格数据时使用此方法比较合适。

fisher卡方检验数据格式

fisher卡方格式一般是汇总格式，比如想要研究A药和B要对疗效的差异性，其数据格式一般如下：（ps：A1表格一定是空的）

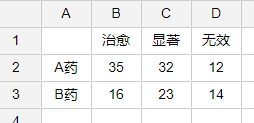
fisher卡方检验操作

【实验/医学研究：fisher卡方】→【拖拽分析项】→点击开始分析；

fisher卡方检验结果一般格式

会提供期望频数和实际频数的分析结果：

03、分层卡方

分层卡方检验说明

分层卡方也叫CMH检验，研究卡方检验，将干扰因素纳入模型，其中X和Y均是类别变量（一般为二分类），比如研究是否吸烟和是否肥胖的差异关系，将性别（男和女）纳入模型内进行分析，此时可以考虑分层卡方。

分层卡方检验数据格式

分层卡方有两种数据格式，一种是不加权数据格式，一种是加权数据格式：

1. 不加权

X为一列（分类变量），Y为一列（分类变量），分层项为一列。

（2）加权

X为一列（分类变量），Y为一列（分类变量），加权项为一列，分层项为一列。

分层卡方检验操作

【实验/医学研究：分层卡方】→【拖拽分析项】→点击开始分析；

（ps：其中加权项是可选的）

分层卡方检验结果一般格式

一般会提供CMH基本说明，以及分层卡方结果汇总等。

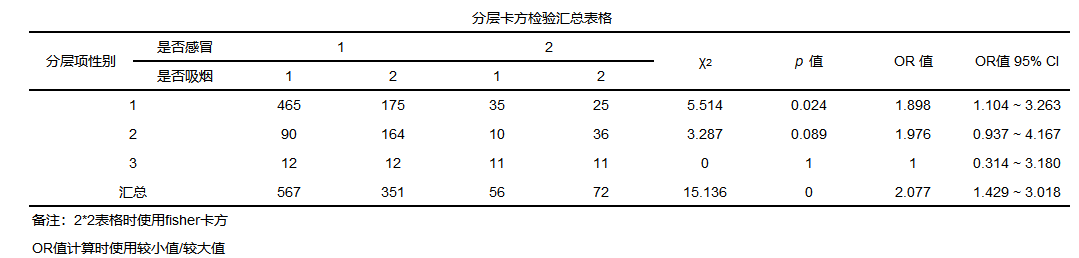
表格说明如下：

04、配对卡方

配对卡方检验说明

配对的定类数据研究差异性，两个变量都为定类数据，且需要数据配对，才可以考虑使用配对卡方进行分析研究，比如研究A方法和B方法对于诊断某病是否有差异（诊断结果分为：阴性和阳性），其中数据为配对数据，此时可以考虑使用配对卡方分析。

配对卡方检验数据格式

配对卡方的数据类型为定类变量，所以有两种类型的数据格式，一种是加权的数据格式，一种是非加权的数据格式：

1. 加权

配对卡方，一般有两列，一个分析项为一列，但是如果是加权格式，加权项为一列，一共有三列。

（2）非加权

如果是非加权的数据格式一个分析项为一列。一共两列，且数据是配对数据。

配对卡方检验操作

【实验/医学研究：配对卡方】→【拖拽分析项】→点击开始分析；

配对卡方检验结果一般格式

一般会提供配对卡方结果以及方法对比，其中如果配对数据的组别为2即配对四表格（2*2），SPSSAU则使用McNemar检验；n*n则使用Bowker检验。

05、卡方拟合优度

卡方拟合优度检验说明

实际数据与预期数据的差异，希望研究数据的实际比例与预期比例是否一致。比如收集100份数据，预期不同性别的比例是4:6，其中搜集的数据为男性为48个女性为52个，进行差异性分析。常用于问卷的选择题中。

卡方拟合优度检验数据格式

卡方拟合优度检验数据格式为一列为一个分析项，一般用于定类数据各项的占比差异情况，一般格式如下：

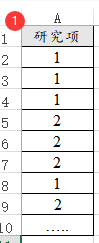
卡方拟合优度检验操作

【实验/医学研究：卡方拟合优度检验】→【拖拽分析项】→点击开始分析；

卡方拟合优度检验结果一般格式

卡方拟合优度检验一般会提供实际频数，期望频数，残差，实际比例，期望比例，卡方值等。

3、秩和检验

01、MannWhitney检验

MannWhitney检验说明

MannWhitney非参数检验一般研究定类数据和定量数据之间的差异，定类数据一般是两组为二分类变量，比如研究不同性别的薪资水平之间的差异等。

MannWhitney检验数据格式

MannWhitney非参数检验的数据格式一般为两列，一列为组别，一列为分析项，数据格式与独立样本t检验类似，与之不同的是二者的应用条件不一样，具体可以参考文章：

MannWhitney检验操作

【通用方法：非参数检验】→【拖拽分析项】→点击开始分析；

MannWhitney检验结果一般格式

一般结果中会提供中位数以及统计量和p值等。

02、KruskalWallis检验

KruskalWallis检验说明

Kruskal-Wallis非参数检验一般是研究定类变量和定类变量之间的差异性，并且定类变量为多分类变量，比如研究学历和薪资之间是否有显著性差异，学历包括本科以下、本科以及本科以上。其数据格式与单因素方差类似。操作与MannWhitney一致（SPSSAU会自动判断分类变量的分类数进而判断使用MannWhitney还是Kruskal-Wallis），其一般形式如下：

一般结果中会提供中位数以及统计量和p值等。

03、配对样本wilcoxon

配对样本wilcoxon说明

配对样本wilcoxon说明检验一般是研究配对的定量数据之前的差异性，比如研究有无广告和产品的销量之间是否有显著性差异。其数据格式与配对样本t检验类似。其操作为：

其一般形式如下：

一般结果中会提供中位数以及统计量和p值等。

04、单样本wilcoxon

单样本wilcoxon说明

单样本wilcoxon说明检验一般是研究检验数据是否与某个数据有明显的差异，比如研究某地区青少年的身高与140cm是否有差异。其数据格式与单样本t检验类似。其操作为：

其一般形式如下：

一般结果中会提供样本量、25分位数、中位数、75分位数以及统计量和p值等。

05、ridit检验

ridit检验说明

Ridit是研究X与Y的差异，X是定类数据，Y是定距数据，比如研究两种药物对慢性病治疗的作用，其中两种药物为定类数据，治疗作用为定距数据。此时可以考虑使用ridit检验。

ridit检验数据格式

一般有两种数据格式，一个是加权数据格式，一个是不加权数据格式，如果不加权数据格式，一行代表一个研究对象，X为一列，Y为一列，如果是加权的数据格式，比如X有2种情况，Y有4个情况，一种有2*4=8种组合，数据信息只有8种组别的汇总项（即加权项），数据格式如下图（由于上传数据带有数据标签，所以新建一个表格）：

ridit检验操作

【实验/医学研究】→【Ridit实验】然后进行分析；

ridit检验结果一般格式

会提供平均ridit值与95％CI和z值p值等。

06、friedman检验

friedman检验说明

Friedman检验可应用于多组配对或相关数据的秩和校验。比如想要分析8名试验对象在4种不同频率声音刺激的反应率是否存在差别。

friedman检验数据格式

一个分析项为一列，比如上述背景“8名试验对象在4种不同频率声音刺激的反应率是否存在差别。”一个声音频率为一列，如下：

friedman检验检验操作

分析路径为点击【实验/医学研究】→【多样本Friedman】然后进行分析：

friedman检验检验结果一般格式

会提供样本量、25分位数、中位数、75分位数以及统计量和p值等。

三、可视化图形

1、可视化图形的选择

数据类型不同其可视化图形选择不同，比如定类数据和定量数据一般可以使用折线图或者柱形图、条形图等，如果是定类和定类数据一般可以使用堆积柱形图或者条形图。

2、折线图

折线图一般分析定类数据格定量数据的差异，比如分析7月和8月30天每天温度变化（一般多分类数据使用较多）。其可以在SPSSAU可视化中进行操作，一般格式如下：

3、柱形图

一般用长方形的进行表示，也叫长条图，可以用来表示定类数据和定量数据之间的差异，定类变量可以为二分类也可以为多分类，其可以在SPSSAU可视化中进行操作，一般格式如下：

4、堆积柱形图（堆积条形图）

用于分析定类数据和定类数据之前的差异，比如两个分类变量对比差异，想要在一个柱形图或者条形图中进行展示占比。其可以在SPSSAU可视化中进行操作，一般格式如下：

四、案例分析

研究者想要观察两种药物对慢性病治疗的作用，共搜集了3000例数据，试分析两种药物在治疗慢性病方面是否有显著差异。部分数据如下，其中药物中1代表A药物，2代表B药物，疗效中1代表无效，2代表好转，3代表明显好转，4代表控制。研究定类数据和定类数据的差异并且是有序定距的数据，考虑使用ridit检验。

1、分析流程

Step1：数据格式

X有2种情况，Y有4个情况，一种有2*4=8种组合，数据信息只有8种组别的汇总项（即加权项），数据格式如下图（由于上传数据带有数据标签，所以新建一个表格）：

Step2：上传数据与操作

上传结果如下：

【实验/医学研究】→【Ridit实验】然后进行分析

Step3与step4以下分别进行说明。

2、解读分析结果

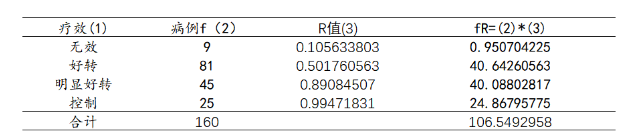
从分析结果来看z值为-7.07，p值小于0.05，说明不同药物对慢性病的治疗有显著差异性，并且从平均Ridit值中可以看出B药物的平均Ridit值(0.666)会明显高于A药物的平均Ridit值(0.500)。中间过程值是如何计算的呢？

3、指标计算

• 平均Ridit值

选择A药物进行分析，B药物同理：

由于以最大值作为参照项，所以A药物组别为标准组，\bar{R}理论上波动于0-1之间，标准组的\bar{R}等于0.5，其它组别都需要参照标准组的R值进行计算。比如B组别：

• 95％CI

以A药物组为例：

z值

n为该组样本量。?��2?可由两组合并数据进行计算，或者近似法以1/12,进行估计，这里不进行计算，感兴趣的可以自行计算。

除此之外，还可以进一步进行图形查看：

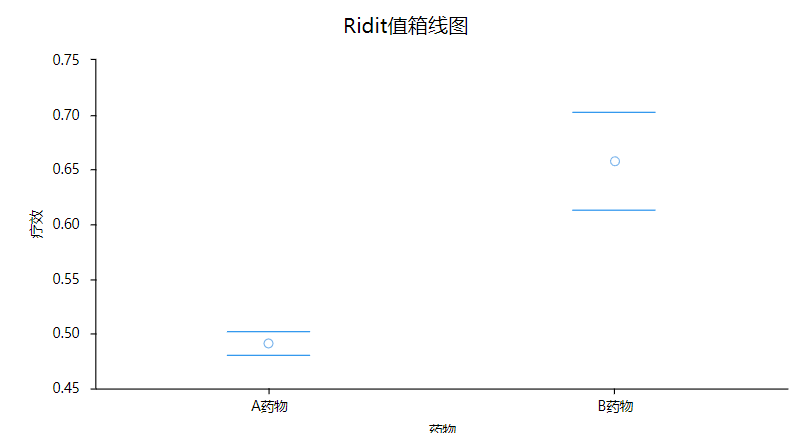
从图形也可以直观看出，B药物的平均Ridit值会明显高于A药物。

SPSSAU?www.spssau.com/?100008000