数据结构——二叉树（先序、中序、后序及层次四种遍历（C语言版））超详细~ (???) Q_Q

? ?

目录

???????? ?

二叉树的定义：

*特殊的二叉树：

?二叉树的性质：

?二叉树的声明：?

?二叉树的先序遍历：

?二叉树的中序遍历：

?二叉树的后序遍历：

二叉树的层序遍历：?

二叉树的节点个数：

二叉树叶节点个数：?

?最后完整代码：

运行结果：?

---

二叉树的定义：

• 二叉树是n（n≥0）个结点的有限集合：
  ① 或者为空二叉树，即n = 0。
  ② 或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
• 特点：①每个结点至多只有两棵子树 ②左右子树不能颠倒（二叉树是有序树）【注意区别：度为2的有序树】

一颗普通的二叉树（栗子）：?

?

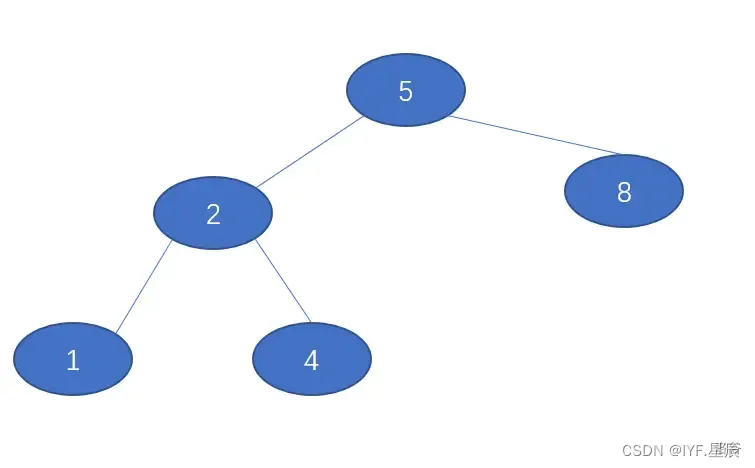*特殊的二叉树：

1.满二叉树：一个二叉树，如果每一个层的节点数都达到最大值，则这个二叉树就是满二叉树。也就是说，一个二叉树的层数为k，且节点总数是（2^k-1）,则它就是满二叉树。

2.完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为k的，有n个节点的二叉树，当且仅当其每一个节点与k都与其深度为k的满二叉树中编号从1至n的节点一一对应时称之为完全二叉树。注意满二叉树是一种特殊的完全二叉树。

?

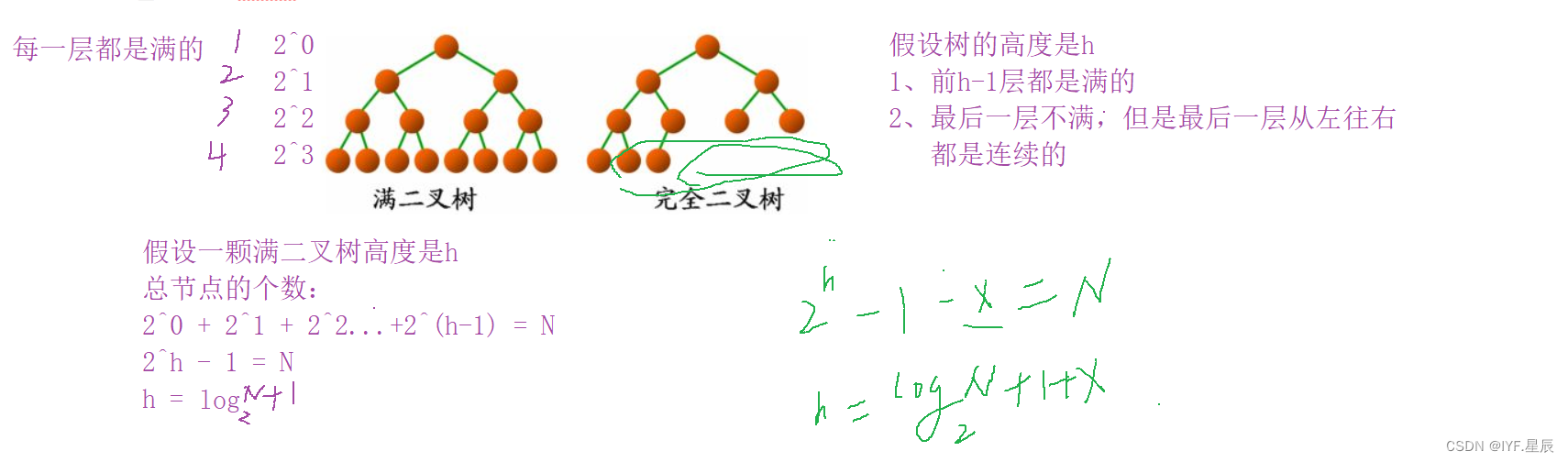?二叉树的性质：

1.若规定根节点的层数为1，则一颗非空二叉树的第i层上最多有2^（i-1）个节点

2.若规定根节点的层数为1，则其深度为h的二叉树的最大节点数是2^h-1

3.对任何一颗二叉树，如果度为0期叶节点个数为n0,度为2的分支节点个数为n2,则有n0=n2+1;

即度为0的叶节点比度为2的分支节点多1

4.若规定根节点的层数为1，具有n个节点的满二叉树的深度h=log2(N+1).

?

?二叉树的声明：?

?

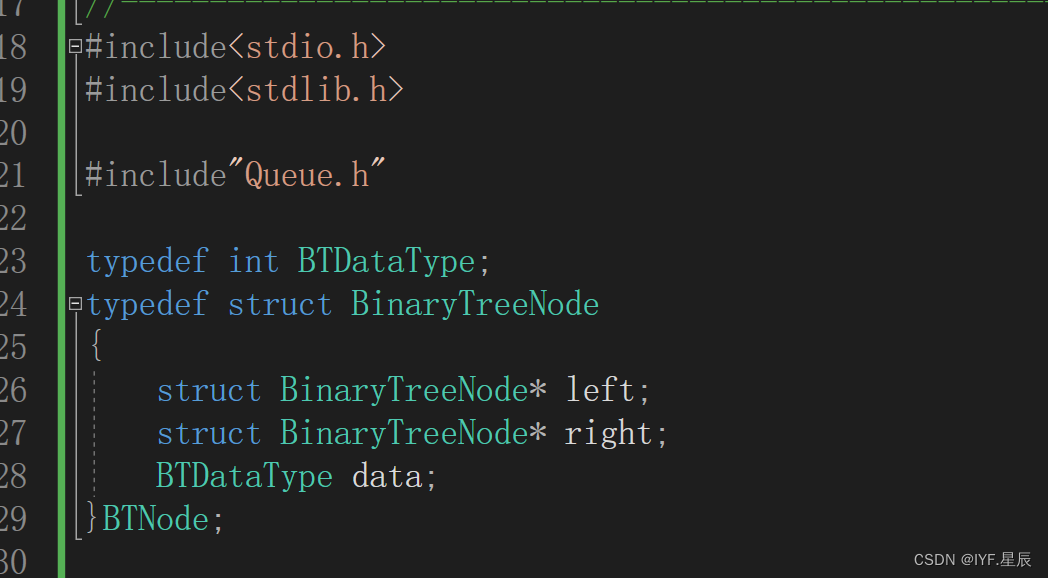为了方便后续的操作与理解，这里给出二叉树的声明?

?二叉树的先序遍历：

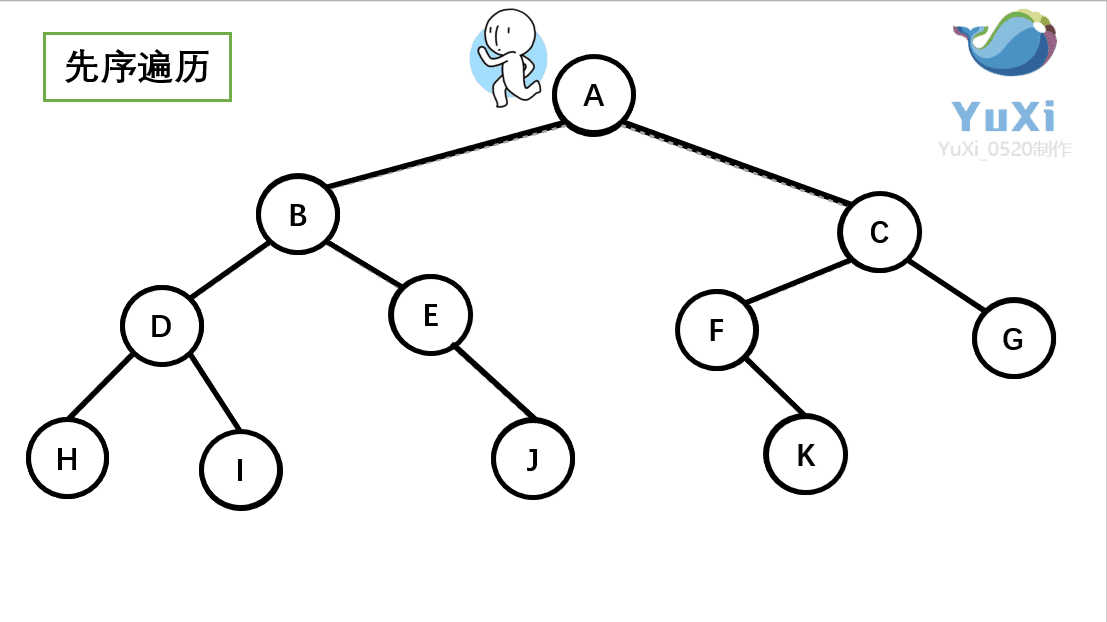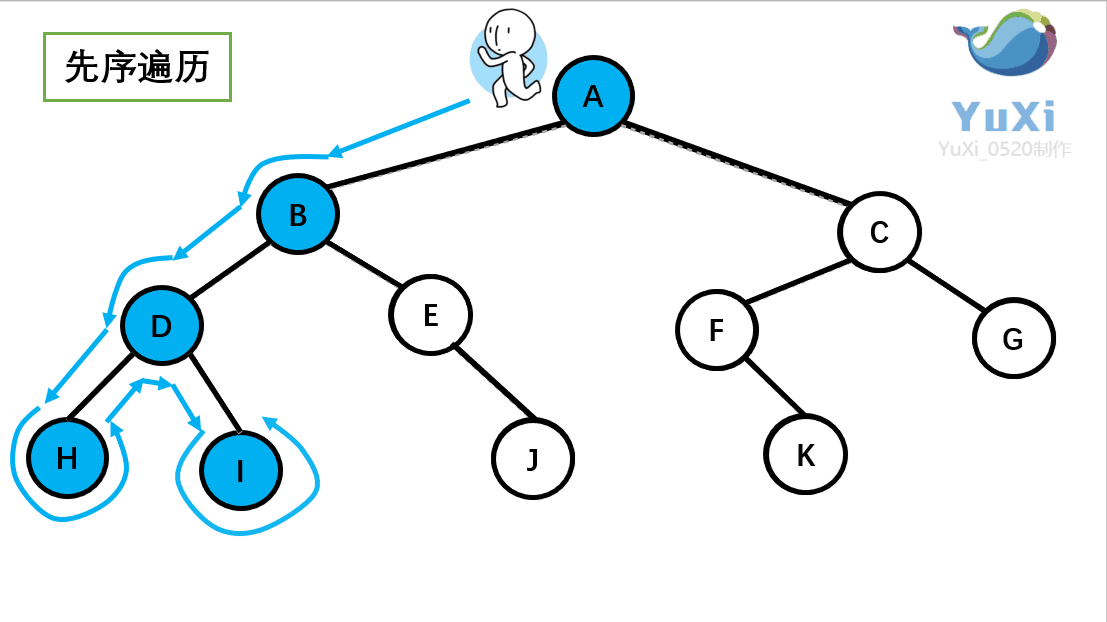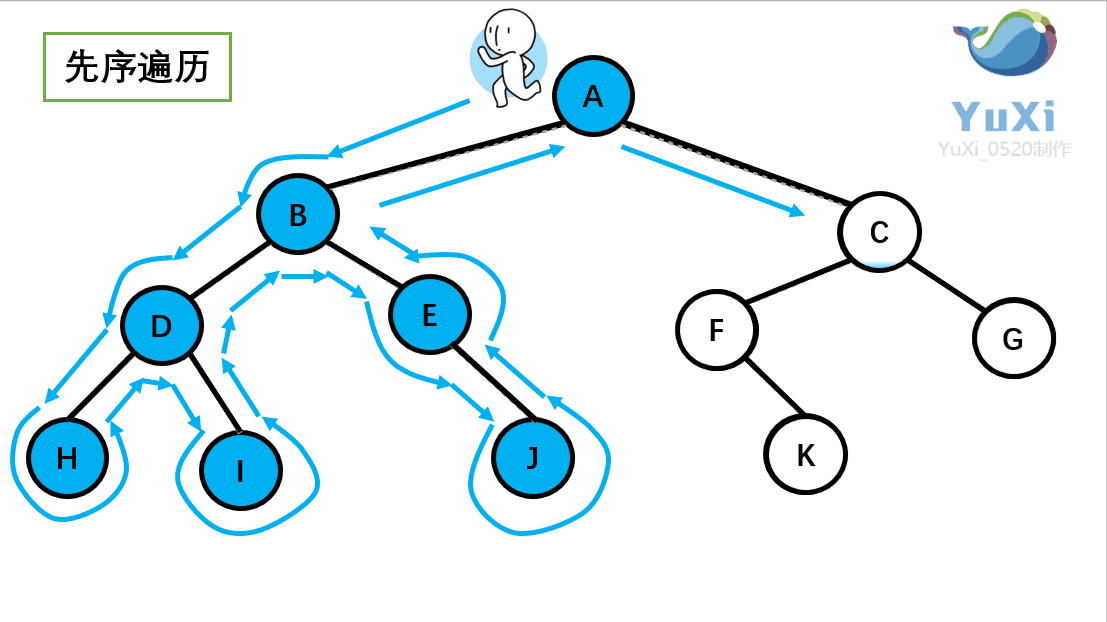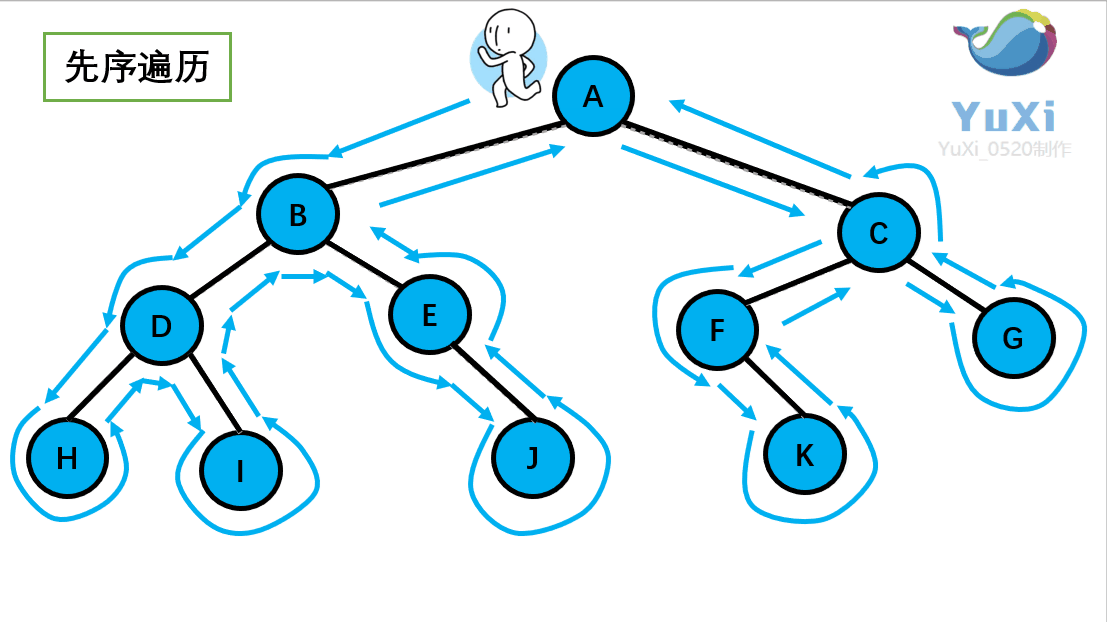
?（1）.先序遍历可以想象为，一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果

代码解释：

?

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

?

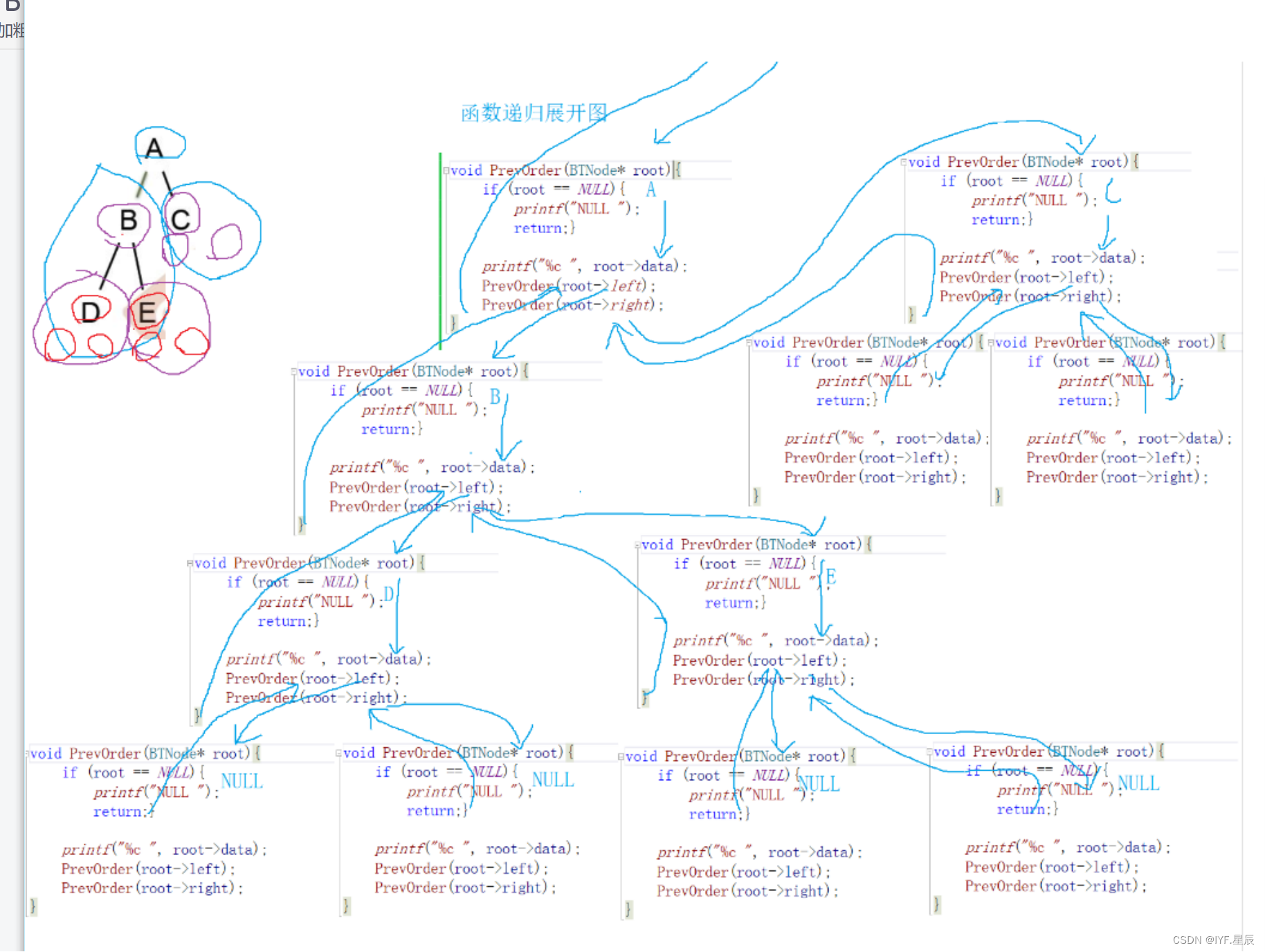根，PrevOrder(root->left) 后PrevOrder(root->right).? ? 即? 根->左子树->右子树 的形式进行遍历。函数进行递推，直到把程序化为不可再分的小的字程序。后回溯依次打印对应数据信息（root->data）.?

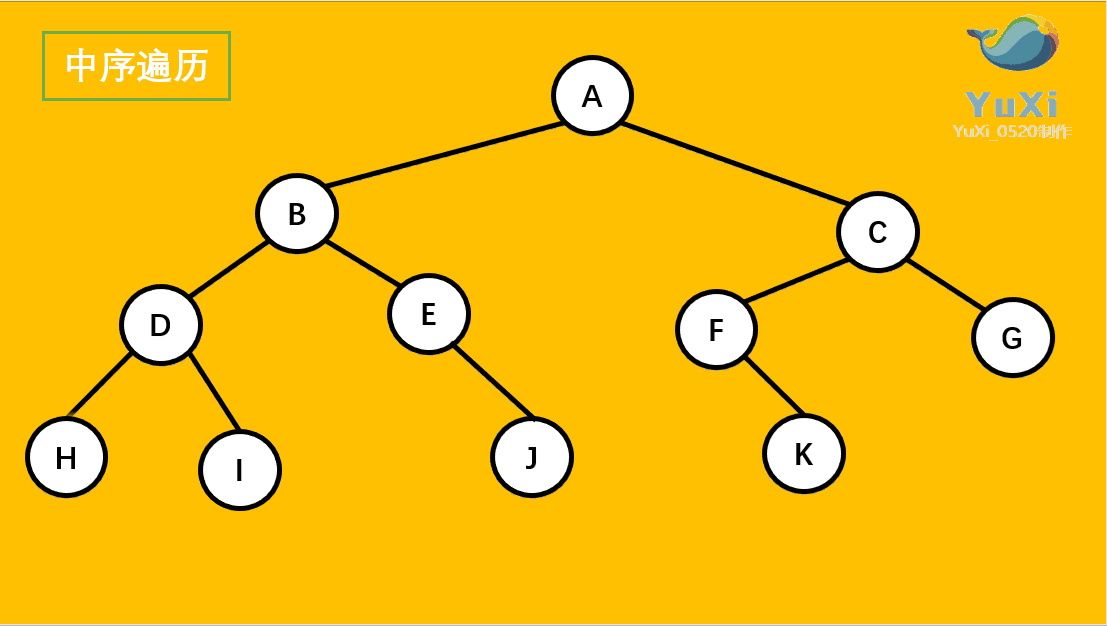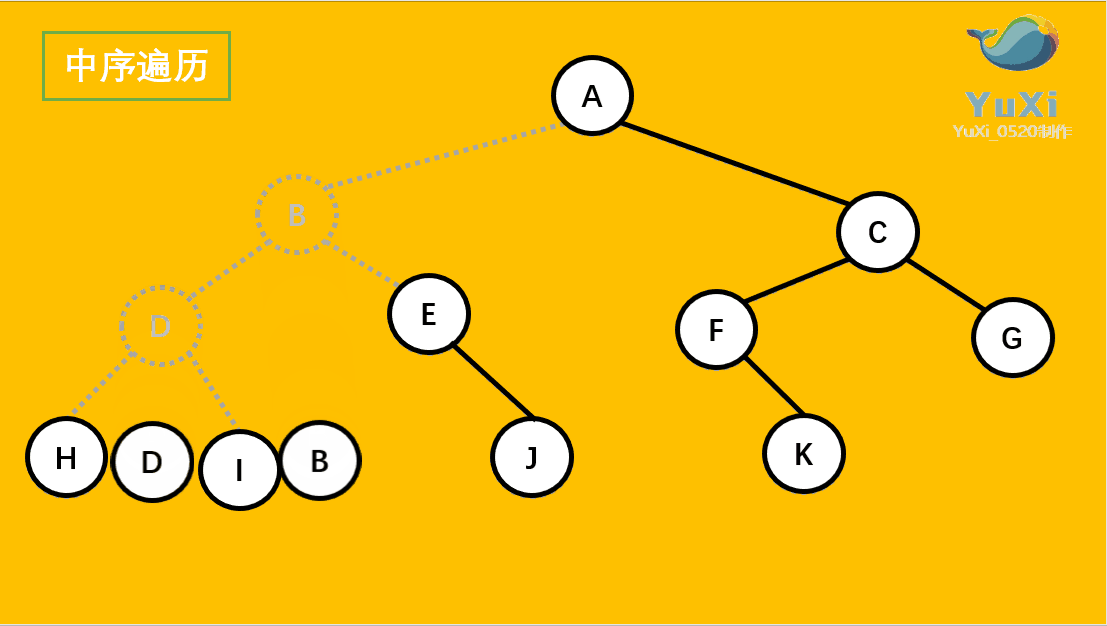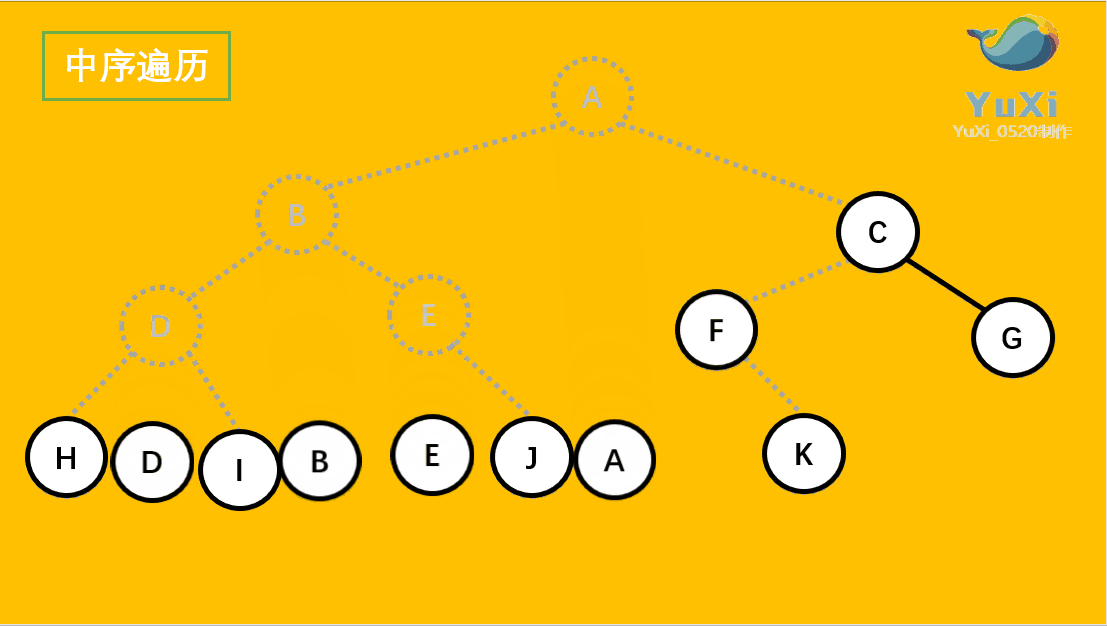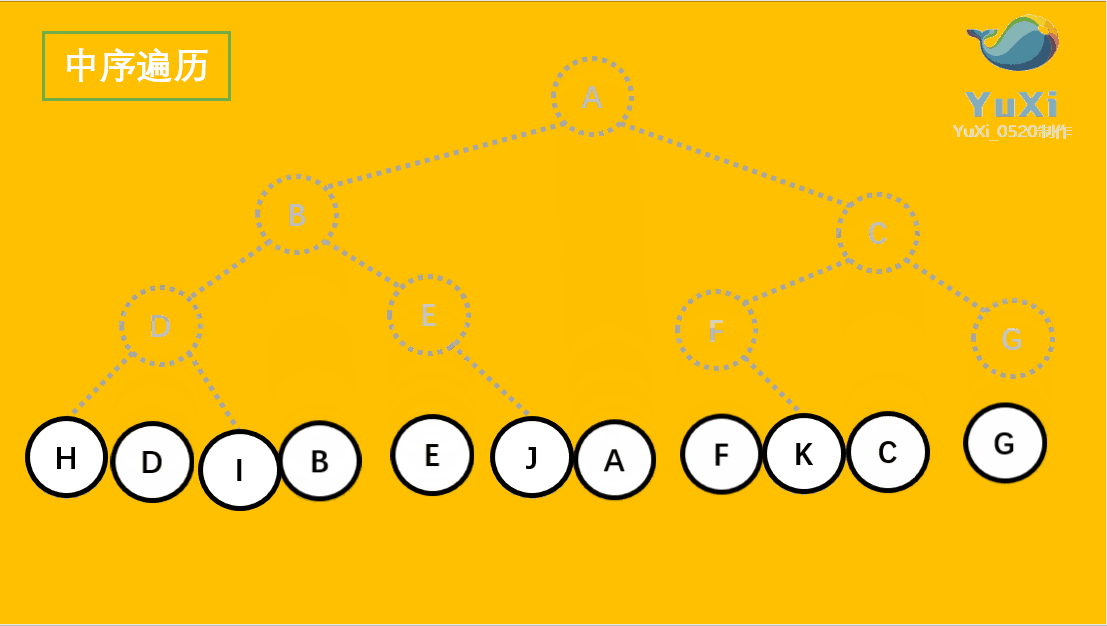
?二叉树的中序遍历：

（2）.中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数，得出的结果便是中序遍历的结果

?

代码解释：

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

函数递归展开图与二叉树先序遍历类似.，这里就不在重复说明.

InOrder(root->left) 根 Inorder(root->right);即? 左子树? 根? ?右子树? 的形式

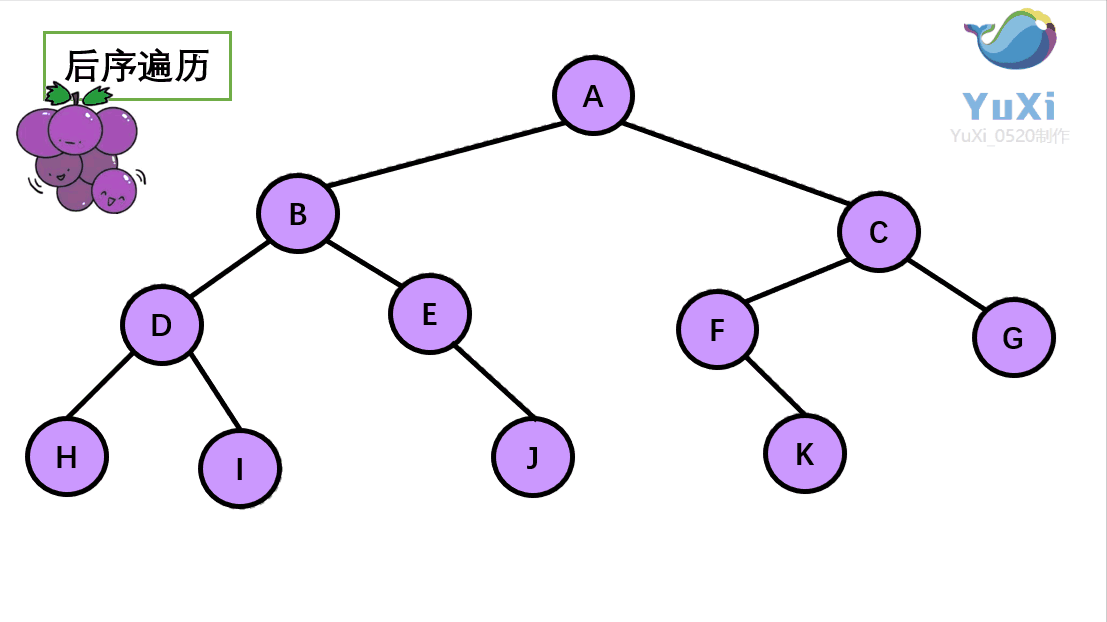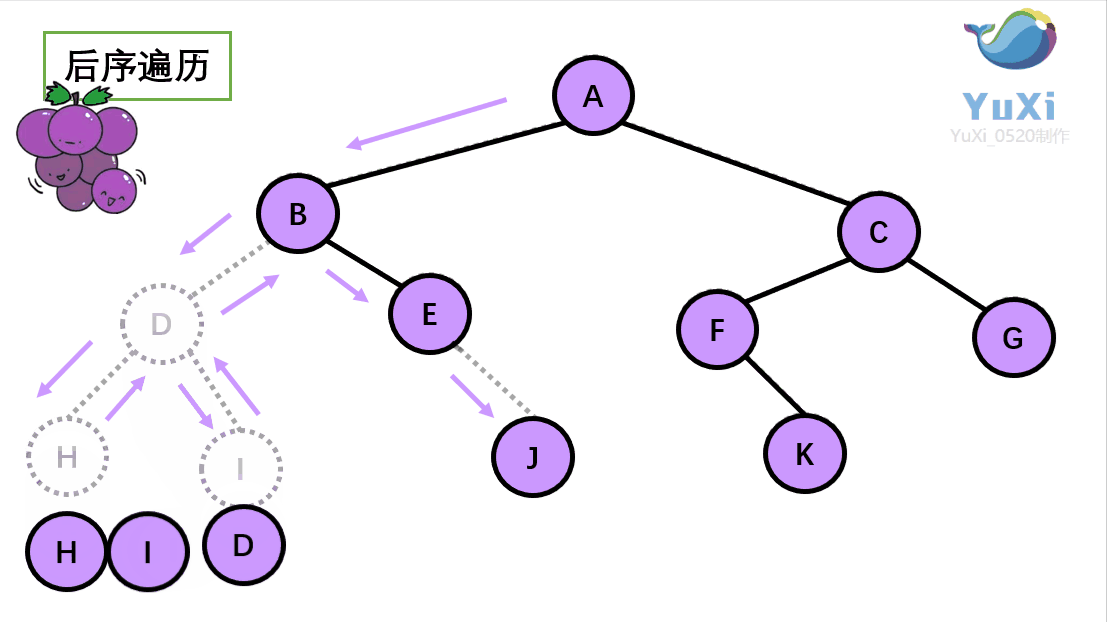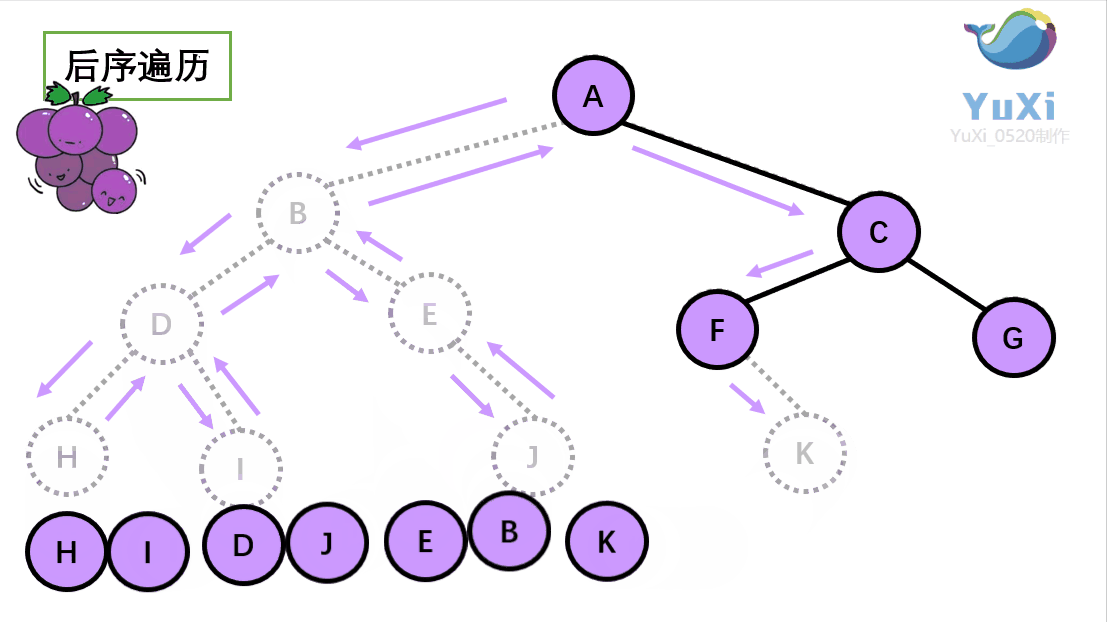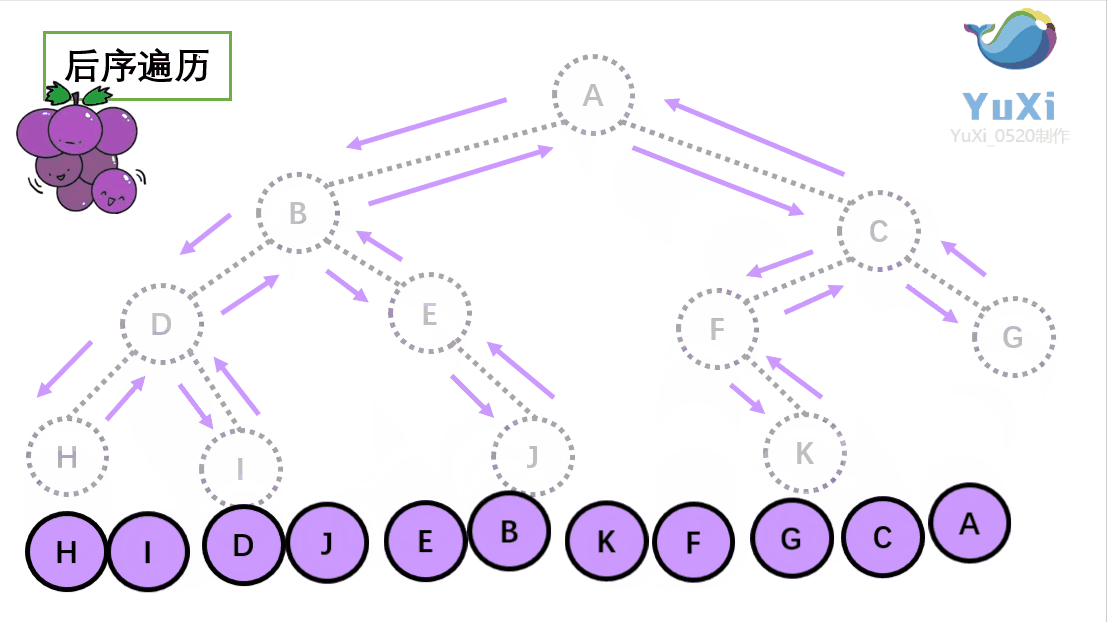
?二叉树的后序遍历：

（3）.后序遍历就像是剪葡萄，我们要把一串葡萄剪成一颗一颗的。如果发现一剪刀就能剪下的葡萄（必须是一颗葡萄）（也就是葡萄要一个一个掉下来，不能一口气掉超过1个这样），就把它剪下来，组成的就是后序遍历了。

?

代码解释：?

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

PostOrder(root->left)? PostOrder(root->right)? 根；即? 左子树? ?右子树? ?根? 的形式?

二叉树的层序遍历：?

顾名思义，就是一层一层的进行遍历。

图解：

?

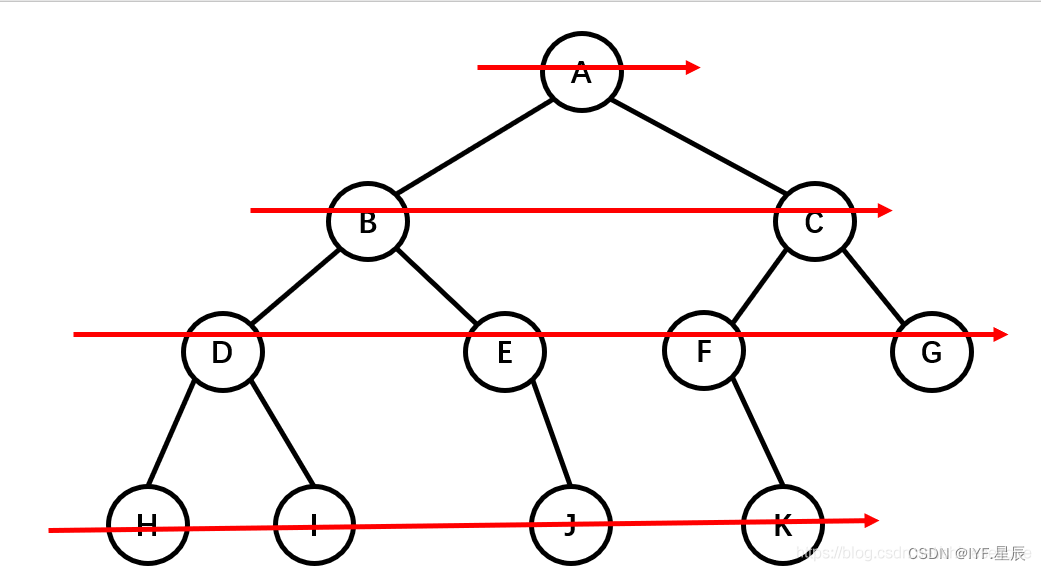
这里用到的队列先进先出的思想，核心思路就是上一层带下一层。如A先进队列，接着A出队列，带着B和C依次进队列，B出带DE，C出带FG……以此类推。?

?

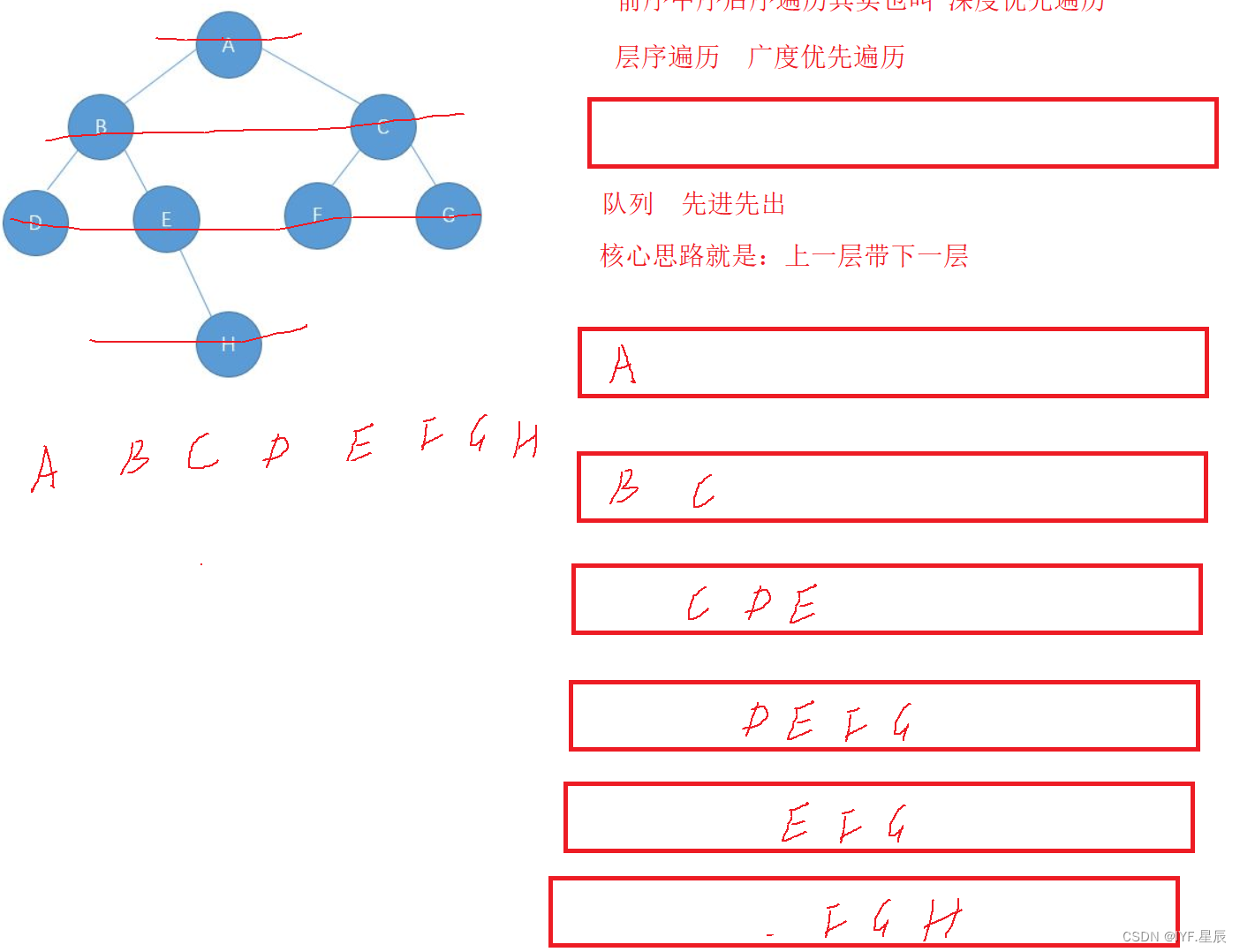?代码解释：

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestory(&q);
}

初始化队列后，依次按上述的方式入数据和删除数据，最后就能得到相应的序列?

?

二叉树的节点个数：

int TreeSize3(BTNode* root)
{
	return root == NULL ? 0 : TreeSize3(root->left) + TreeSize3(root->right) + 1;
}

分为最小的子程序即根的左右子树节点个数加本身。

也就是 TreeSize3(root->left)+TreeSize3(root->right)+1;

二叉树叶节点个数：?

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

?最后完整代码：

#include<stdio.h>
#include<stdlib.h>

#include"Queue.h"

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}
int size = 0;
void TreeSize1(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	else size++;
	TreeSize1(root->left);
	TreeSize1(root->right);
}

void TreeSize2(BTNode* root,int* psize)
{
	if (root == NULL)
		return;
	else
	{
		++(*psize);
	}
	TreeSize2(root->left,psize);
	TreeSize2(root->right, psize);
}

int TreeSize3(BTNode* root)
{
	return root == NULL ? 0 : TreeSize3(root->left) + TreeSize3(root->right) + 1;
}

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestory(&q);
}

int main()
{
	BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;

	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;

	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;

	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;

	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;

	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;

	PrevOrder(A);
	printf("\n");

	PostOrder(A);
	printf("\n");

	LevelOrder(A);
	printf("TreeLeafSize:%d\n", TreeLeafSize(A));
	printf("TreeSize:%d\n", TreeSize3(A));
	printf("TreeSize:%d\n", TreeSize3(B));
	return 0;
}

注意这里TreeSize1,TreeSize2,TreeSize3只是计算二叉树节点个数的三种方法。

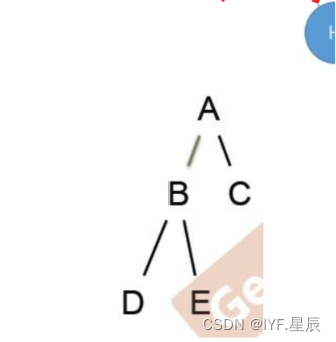
这里创建的二叉树为：

?

运行结果：?

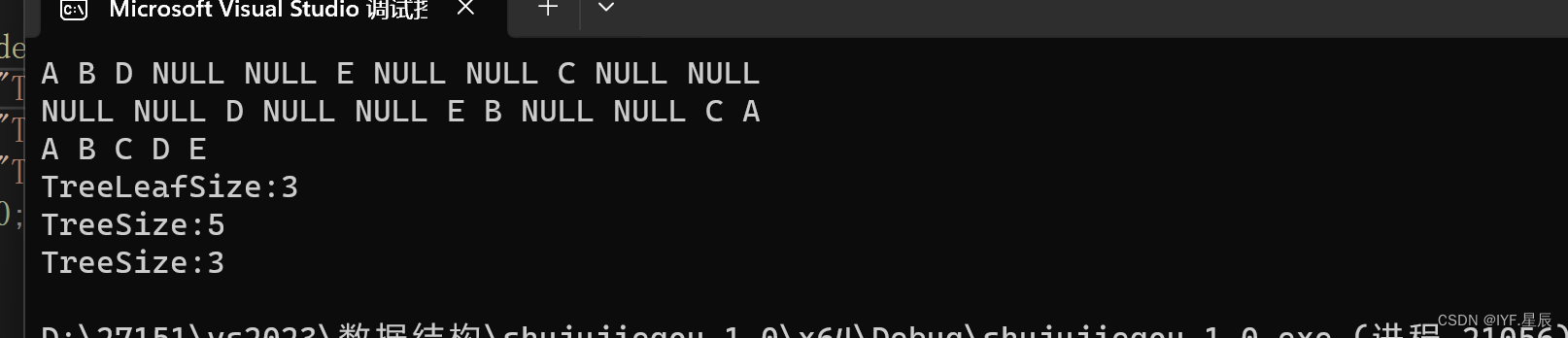
博客到这里也是结束了，喜欢的小伙伴可以点赞加关注支持下博主，这对我真的很重要~~