多重背包问题的二进制优化
发布时间:2024年01月15日
题目:
样例:
|
| 10 |
思路:
? ? ? ? 对于朴素版的多重背包问题DP,由于朴素版的多重背包问题DP是三层循环,所以合适范围数据范围是在100左右,当数据范围再多 一个 10倍的时候,朴素版的多重背包问题就会 TLE 了。
? ? ? ? 朴素版的多重背包问题,原理的三层循环中,有一层循环是作为取多少个当前这个物品的原理,达到完成dp状态的转移。
? ? ? ? 我们二进制优化这个朴素版的多重背包问题,就是优化掉我们?取多少个当前这个物品 的这一层循环。
? ? ? ? 至于为什么要用二进制来优化呢?
? ? ? ? 这是因为,我们取物品的时候,就有取这个物品,和不取两种操作,其中 核心在于取多少个为合适, 二进制中各位是由? 1248... 巧妙的分成了多个部分,每一部分的组合就可以到达我们预期。
? ? ? ? 比如:? ?
| 目标取 的个数 | 各位组合 |
| 1???????? | 1 |
| 2 | 2 |
| 3 | 1 + 2 |
| 4 | 4 |
| 5 | 1 + 4 |
| 6 | 2 + 4 |
| 7???????? | 1 + 2 + 4 |
所以我们可以将物品的数量分成二进制位的组合作为新一个物品。
代码详解如下:
????????
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
#include <algorithm>
#include <unordered_map>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) x.begin(),x.end()
#pragma GCC optimize(3,"Ofast","inline")
#define IOS std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10;
// 物品结构体
struct Goods
{
// v 作为物品体积
// w 作为物品价值
int v,w;
inline Goods(int a,int b):v{a},w(b){}
};
inline void solve()
{
vector<Goods>goods; // 存储物品
int n,m,v,w,s;
cin >> n >> m;
for(int i = 1;i <= n;++i)
{
cin >> v >> w >> s;
// 将 数量 c 分解组合 为 二进制位数的大小 的价值和容量
for(int j = 1;s >= j;j<<=1)
{
s -= j;
goods.emplace_back(Goods(v*j,w*j)); // 存储好每个组合的物品
}
// 如果按二进制各位的分解到最后,分解不了更高位后
if(s > 0) goods.emplace_back(Goods(v*s,w*s)); // 就再次存储好我们剩余的数量组合
}
vector<int>dp(m + 1,0); // dp数组
// 下面就是正常的 dp 取 与 不取的 01 背包dp
for(Goods &now:goods)
{
// now 作为当前物品
for(int j = m;j >= now.v;--j)
{
dp[j] = max(dp[j],dp[j - now.v] + now.w);
}
}
cout << dp[m] << endl;
}
signed main()
{
// freopen("a.txt", "r", stdin);
IOS;
int _t = 1;
// cin >> _t;
while (_t--)
{
solve();
}
return 0;
}最后提交: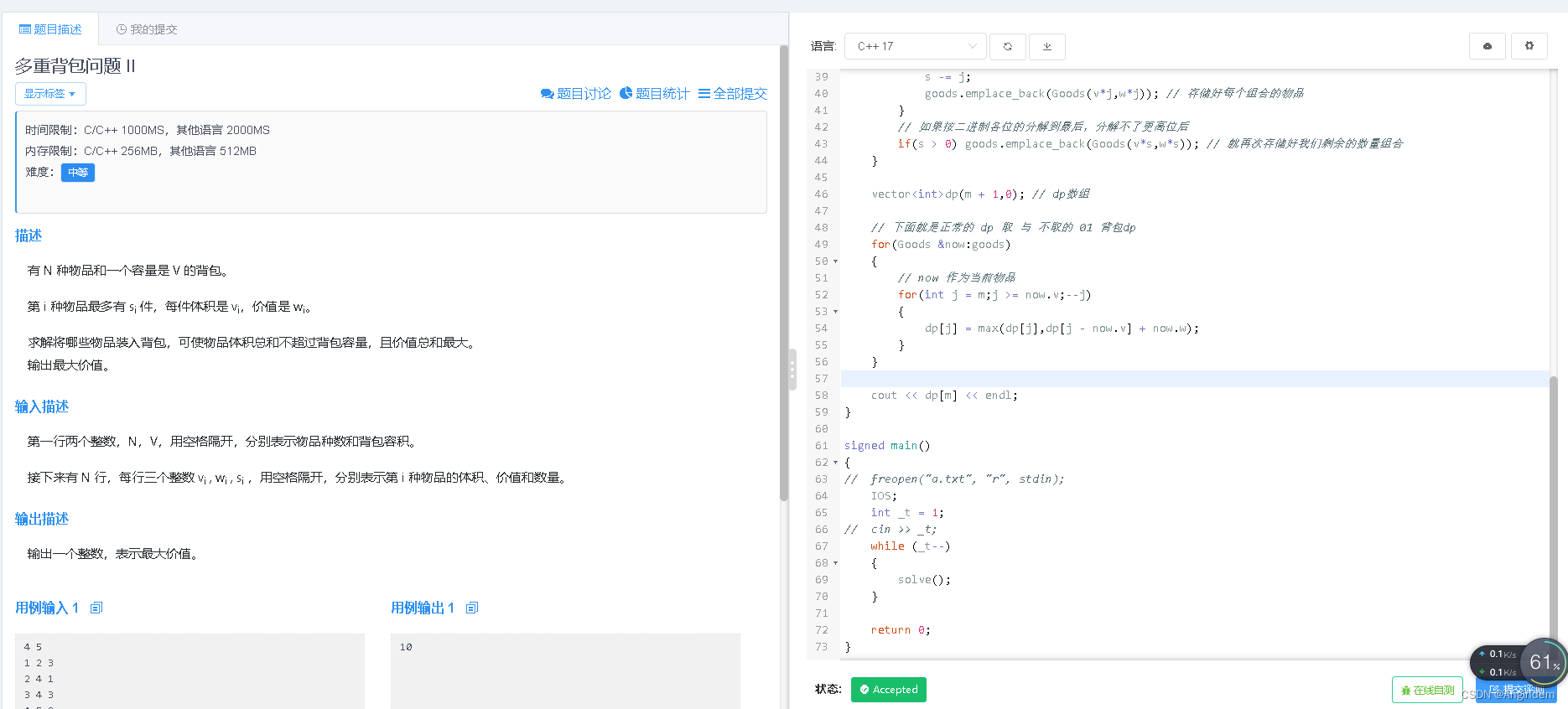 ???????
???????
文章来源:https://blog.csdn.net/hacker_51/article/details/135606101
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- ubuntu18.04 64 位安装笔记——备赛笔记——2024全国职业院校技能大赛“大数据应用开发”赛项——任务2:离线数据处理
- Linux 入门概述
- meter报OOM错误,如何解决?
- 直播怎么录制视频?轻松提升视频质量!
- 设计模式的艺术P1基础—2.4-2.11 面向对象设计原则
- Git常用命令diff和mv
- PPI+机器学习+免疫浸润+实验验证,如此简单也能发4+
- 整理composer安装版本的python脚本
- 7-18 职工排序题(Java for PTA)
- easyexcel怎么读取excel合并单元格数据