python练习题

1. 找出1到20内的所有质数

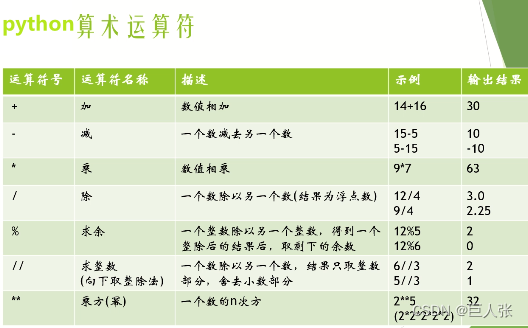
提示：质数是指大于1的自然数，除了1和它本身以外没有任何正因数（除了1和它本身外不能被其他整数整除）。换句话说，质数是只有两个正因数的数，这两个因数就是1和它自己。

for num in range(2, 21):  # 起始值为2，对于范围在2到20的每一个数字
    for i in range(2, num):  # 对于从2到num-1的每一个数字
        if num % i == 0:  # 如果num能被i整除
            break  # 退出内层循环，说明num不是质数
    else:
        print(num)  # 如果内层循环完整执行（即未中断），则说明num是质数，打印输出
# 结果：2、3、5、7、11、13、17、19

假如用JavaScript，如何实现？

 for (let num = 2; num <= 20; num++) {
   let isPrime = true;
   for (let i = 2; i < num; i++) {
     if (num % i === 0) {
       isPrime = false;
       break;
     }
   }
   if (isPrime) {
     console.log(num);
   }
 }

2. 找出整数12和18的最大公约数

在Python中，你可以使用欧几里得算法（也称为辗转相除法）来找出两个整数的最大公约数。这个算法的基本思想是：用较大的数除以较小的数，然后用余数去除较小的数，如此反复，直到余数为0，最后的除数就是这两个数的最大公约数。

下面是实现这个算法的Python代码：

def gcd(a,b):
    if b==0:
        return a
    return gcd(b,a%b)
print(gcd(12,18))

3. 找出整数4和5的最小公倍数

在Python中，我们可以使用math库中的gcd函数来找到两个数的最大公约数，然后用这个结果来计算最小公倍数。这是因为两个数的乘积除以它们的最大公约数等于它们的最小公倍数。

import math  
  
def lcm(a, b):  
    return abs(a*b)
  
print(lcm(4, 5))  # 输出20

4.利用python打印一个棱形。

num = 4  
up_str = ""  
  
# 正三角形  
for i in range(num):  
    for _ in range(num - i - 1):  
        up_str += " "  
    for _ in range(2 * i + 1):  
        up_str += "*"  
    up_str += "\n"  
  
# 倒三角形  
for i in range(num - 1, 0, -1):  
    for _ in range(num - i):  
        up_str += " "  
    for _ in range(2 * i - 1):  
        up_str += "*"  
    up_str += "\n"  
  
print(up_str)

结果：

如果用JavaScript实现，代码如下：

 // 打印的倍数
 let num = 4;
 let upStr = "";

 // 正三角形
 for (var i = 0; i < num-1; i++) {
   for (var j = num; j > i + 1; j--) {
     upStr += " ";
   }
   for (var k = 0; k < 2 * i + 1; k++) {
     upStr += "*";
   }
   upStr += "\n";
 }
 
 // 倒三角形
 for (var i = num; i > 0; i--) {
   for (var j = num; j > i; j--) {
     upStr += " ";
   }
   for (var k = 0; k < 2 * i - 1; k++) {
     upStr += "*";
   }
   upStr += "\n";
 }
 console.log(upStr);

4. 打印乘法口诀表

for i in range(1,10):
    for j in range(1,i+1):
        print(f'\t{i}*{j}={i*j}',end=' ')
    print('\n')

5. 斐波那契数

斐波那契数 ：该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。

n = input('please input number: ')
n = int(n)
def fn(n):
    if n==0:
        return 0;
    list = [0,1]
    for i in range(2,n+1):
        list.append(list[i-1]+list[i-2]);
    return list[-1]
print(fn(n))

6. 冒泡排序

思路：

• 比较所有相邻的元素，如果第一个比第二个大，则交换他们。
• 一轮下来，可以保证最后一个数是最大的。
• 以此类推，执行n-1轮，就可以完成排序。

list = [5,2,9,1,3,4]
L = len(list)
def fn(list):
    for i in range(0,L):
        for j in range(0,L-1-i):
            if list[j]>list[j+1]:
                list[j],list[j+1] = list[j+1],list[j]
    return list
print(fn(list))

7. 选择排序

• 方法一，思路：

• 找到数组中的最小值，把他更换到列表中的第一位。（具体做法：先假设第一数为最小值，记录它的索引值，将第一数和第二个数作比较，如果第一个数大于第二个数则交换他们，此时最小值变为两者中较小的一个数；接着用最小值和下一个数继续比较，如果最小值大于下一个数，则交换他们的值，依次循环比较，一轮比较下来，最小值就会被找到，并且更换到最开始的位置。
• 接着找到第二小的值，把他更换到列表中的第二位。
• 以此类推，执行n-1轮，就可以完成排序。

代码如下：

list = [5,2,9,1,3,4]
L = len(list)
def fn(list):
    for i in range(0,L-1):
        min = i
        for j in range(i,L):
            if list[min]>list[j]:
                list[j],list[min]=list[min],list[j]
    return list
print(fn(list))

• 方法二，思路：

• 找到数组中的最小值，把他更换到列表中的第一位。（具体做法：与方法一类似，只不过内层循环每次都是去记录最小值所在的位置，一轮比较结束后，可以获得最小值所在的位置，然后再和最开头的元素进行交换。
• 接着找到第二小的值，把他更换到列表中的第二位。
• 以此类推，执行n-1轮，就可以完成排序。

list = [5,2,9,1,3,4]
L = len(list)
def fn(list):
    for i in range(0,L-1):
        min = i
        for j in range(i,L-1):
            if list[min]>list[j+1]:
                min = j+1
        list[i],list[min]=list[min],list[i]
    return list
print(fn(list))       

8. 插入排序

思路：

• 从第二个数开始往前比。
• 如果第二个数比第一个数小，则需要交换他们的位置；再让第三个数和前两个数依次比较（从第二个数开始对比），如果第三个数比其中任何一个数小，则同样需要交换位置。
• 以此类推，进行到最后一个数。

举例：假如已经进行到31这个数了，31前面的数我们已经插入排序完毕了；那么对于31这个数，我们需要先将其与93比较，31<93，交换位置；接着比较31<77，交换位置；接着比较31<54，交换位置；接着比较31>26，不需要交换位置了，此时内层循环可以结束了。

初版代码：

list = [5,2,9,1,3,4]
L = len(list) 
for j in range(1,L):
    while j>0:
        if list[j]<list[j-1]:
            list[j],list[j-1]=list[j-1],list[j]
        j-=1
        print(list)

结果：

注意：从打印结果看，我们会发现内层循环会多了一些不必要的排序的比较，比方说：现在列表的顺序是这样的：[2, 5, 9, 1, 3, 4]，但我们对9这个数字做插入排序比较的时候，会发现9>5，不需要交换位置；从代码的书写来看，j递减一之后，还会做5和2的比较，虽然5>2，不需要交换位置，但是这样的打印次数就增多了，所以代码是存在优化的空间的。也就是所，对于已经排序好的数字，其实我们是不再需要做对比的，这样可以减少内层循环，即while循环的次数。

代码改进：

list = [5, 2, 9, 1, 3, 4]
L = len(list)
for j in range(1, L):
    while j > 0 and list[j] < list[j - 1]:
        list[j], list[j - 1] = list[j - 1], list[j]
        j -= 1
        print(list)

结果：

9. 顺序查找

思路：

• 遍历列表。
• 找到跟目标值相等的元素，就返回他的下标。
• 遍历结束后，如果没有搜索到目标值，就返回-1。

list = [5,2,9,1,3,4]
L = len(list)
num = input('请输入您要查找的数字：')
num = int(num)
for i in range(0,L):
    if num==list[i]:
        print('您查找到的数字其索引值为：',i)
        break
else:
    print('找不到该数字!')

注意：该else语句与for循环相关联，而不是与if语句相关联。如果for循环完成时没有遇到break，则意味着在列表中未找到该数字，else将会被执行。这个写法应该是 Python 特有的，与其他编程语言略有不同。

10. 二分查找

【注意】：二分查找的前提是列表是排序好的。

思路：

• 从数组的中间元素开始，如果中间元素正好是目标值，则搜索结束。
• 如果目标值大于或者小于中间元素，则在大于或小于中间元素的那一半数组中搜索。

list = [1, 2, 3, 4, 5, 9]
L = len(list)
left = 0
right = L-1
target = 9
while left<=right:
    mid = (left+right)//2 #地板除：只保留整数
    if list[mid]<target:
        left = mid+1
    elif list[mid]>target:
        right = mid-1
    else:
        print('您查找的数字其索引值为：',mid)
        break
else:
    print('找不到该数字!')

【注意】：上面while循环的判断是left<=right;避免查找的元素处于边缘位置，而没有查找到的情况。

11. 画图形

• （1）正方形

import turtle
turtle.forward(100)
turtle.left(90)
turtle.forward(100)
turtle.left(90)
turtle.forward(100)
turtle.left(90)
turtle.forward(100)

解释：

• import turtle: 这行代码导入了turtle模块，它是一个非常基础的绘图库，常用于教学和简单的图形绘制。
• turtle.forward(100): 这行代码让海龟（turtle，也就是绘图的光标）向前移动100个单位。在默认情况下，这个单位是像素，但也可以根据需要设置其他单位。
• turtle.left(90): 这行代码让海龟向左转90度。在绘图时，这通常意味着海龟会逆时针旋转90度。

• （2）传统五角星
  

import turtle
turtle.forward(100)
turtle.right(144)
turtle.forward(100)
turtle.right(144)
turtle.forward(100)
turtle.right(144)
turtle.forward(100)
turtle.right(144)
turtle.forward(100)
turtle.shape('turtle') 

• 结果示意图：
  
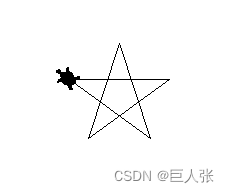
  解释：

• turtle.shape(‘turtle’)：这行代码将这个光标的形状设置为一个传统的“turtle”形状，这通常是一个带有圆形壳的小乌龟。这个功能使得在绘制图形时，用户可以看到一个有趣的、像真的小乌龟一样的光标在屏幕上移动，增加了绘图的乐趣和互动性。turtle.shape()函数支持多种预定义的形状，包括：“arrow”：向右的等腰三角形。 “turtle”：传统的乌龟形状。 “circle”：实心圆。 “square”：实心正方形。 “triangle”：向右的正三角形。 “classic”：箭头。

• （3）小雪人
  
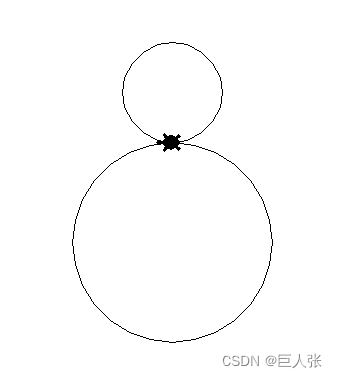
• 方法一：

import turtle
turtle.shape('turtle')
turtle.circle(50) # 逆时针,50代表半径
turtle.left(180) # 逆时针旋转180度
turtle.circle(100)

• 方法二：

import turtle
turtle.shape('turtle')
turtle.circle(50) # 逆时针
turtle.circle(-100) # 顺时针

12.水仙花数

• 水仙花数：指一个 n 位数（n≥3），它的每个位上的数字的 n 次幂之和等于它本身。例如，153是一个水仙花数，因为1^3 + 5^3 + 3^3 = 153。
• 题目：找出100~999整数中的所有水仙花数
  
• 方法一：使用while循环

num = 100
while num<1000:
    a = int(num/100)
    b = int(num%100/10)
    c = int(num%10)
    if a**3+b**3+c**3==num:
        print(num,'是一个水仙花数')
    num+=1

• 方法二：使用for循环

for x in range(100,1000):
    a = int(x/100) #百位数
    b = int(x%100/10) #十位数
    c = int(x%10) #个位数
    if a**3+b**3+c**3==x:
        print(x,'是一个水仙花数')
    x+=1

结果：