Floyd - Warshall算法

顶点

public class Vertex {
 ? ?String name;
 ? ?List<Edge> edges;
 ? ?
 ? ?// 拓扑排序相关
 ? ?int inDegree;
 ? ?int status; // 状态 0-未访问 1-访问中 2-访问过，用在拓扑排序
?
 ? ?// dfs, bfs 相关
 ? ?boolean visited;//是否被访问过
?
 ? ?// 求解最短距离相关
 ? ?private static final int INF = Integer.MAX_VALUE;
 ? ?int dist = INF;
 ? ?Vertex prev = null;

    public Vertex(String name){this.name = name;}

    public String getName{return name;}

    @Override 
    public String toString(){return name + '('+dist+')';}

    @Override
    public boolean euqals(Object o){
        if(this == o)return true;
        if(0==null||getClass()!=o.getClass())return false;

        Vertex vertex = (Vertex) o;
        return Objexts.equals(name,Vertex.name);
    }
    @Override
    public int hashCode(){
        return name!=null?name.hashCode():0;
    }

边

public class Edge {
?
 ? ?Vertex linked;
 ? ?int weight;
?
 ? ?public Edge(Vertex linked) {
 ? ? ? ?this(linked, 1);
 ?  }
?
 ? ?public Edge(Vertex linked, int weight) {
 ? ? ? ?this.linked = linked;
 ? ? ? ?this.weight = weight;
 ?  }
}

?可以处理负边 但是不能处理负环

4+-2+2+-1=3 所以没有负环

public class FloydWarshall {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");

        v1.edges = List.of(new Edge(v3, -2));
        v2.edges = List.of(new Edge(v1, 4), new Edge(v3, 3));
        v3.edges = List.of(new Edge(v4, 2));
        v4.edges = List.of(new Edge(v2, -1));
        List<Vertex> graph = List.of(v1, v2, v3, v4);

        /*
                k=0直接连通
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   3   ∞
            v3  ∞   ∞   0   2
            v4  ∞   -1  ∞   0

看上面那副图的权重

                k=1 借助v1到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   2   ∞
            v3  ∞   ∞   0   2
            v4  ∞   -1  ∞   0

                k=2 借助v2到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   2   ∞
            v3  ∞   ∞   0   2
            v4  3   -1  1   0

                k=3 借助v3到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  0
            v2  4   0   2   4
            v3  ∞   ∞   0   2
            v4  3   -1  1   0

                k=4 借助v4到达其它顶点
                v1  v2  v3  v4
            v1  0   -1   -2  0
            v2  4   0   2   4
            v3  5   1   0   2
            v4  3   -1  1   0
         */
        floydWarshall(graph);
    }

    static void floydWarshall(List<Vertex> graph) {
        int size = graph.size();//顶点个数
        int[][] dist = new int[size][size];
        Vertex[][] prev = new Vertex[size][size];//从哪里来
        // 1）初始化
        for (int i = 0; i < size; i++) {
            Vertex v = graph.get(i); // v1 (v3)内层循环顶点
            Map<Vertex, Integer> map = v.edges.stream().collect(Collectors.toMap(e -> e.linked, e -> e.weight));
            for (int j = 0; j < size; j++) {
                Vertex u = graph.get(j); // v3  外层循环顶点
                if (v == u) {
                    dist[i][j] = 0;//相同顶点
                } else {
                    dist[i][j] = map.getOrDefault(u, Integer.MAX_VALUE);
                    prev[i][j] = map.get(u) != null ? v : null;//更新上一个顶点
                }
            }
        }
        print(prev);
        // 2）看能否借路到达其它顶点
        /*
            v2->v1          v1->v?
            dist[1][0]   +   dist[0][0]
            dist[1][0]   +   dist[0][1]
            dist[1][0]   +   dist[0][2]
            dist[1][0]   +   dist[0][3]
         */
        for (int k = 0; k < size; k++) {
            for (int i = 0; i < size; i++) {
                for (int j = 0; j < size; j++) {
//                    dist[i][k]   +   dist[k][j] // i行的顶点，借助k顶点，到达j列顶点
//                    dist[i][j]                  // i行顶点，直接到达j列顶点
                    if (dist[i][k] != Integer.MAX_VALUE &&
                            dist[k][j] != Integer.MAX_VALUE &&
                            dist[i][k] + dist[k][j] < dist[i][j]) {
                        dist[i][j] = dist[i][k] + dist[k][j];
                        prev[i][j] = prev[k][j];
                    }
                }
            }
//            print(dist);
        }
        print(prev);
        for(int i=0;i<size;i++){
            for(int j=0;j<size;j++){
                path(prev,graph,i,j);
            }
        }
    }

    static void path(Vertex[][] prev, List<Vertex> graph, int i, int j) {
        LinkedList<String> stack = new LinkedList<>();
        System.out.print("[" + graph.get(i).name + "," + graph.get(j).name + "] ");
        stack.push(graph.get(j).name);
        while (i != j) {
            Vertex p = prev[i][j];
            stack.push(p.name);
            j = graph.indexOf(p);
        }
        System.out.println(stack);
    }

    static void print(int[][] dist) {
        System.out.println("-------------");
        for (int[] row : dist) {
            System.out.println(Arrays.stream(row).boxed()
                    .map(x -> x == Integer.MAX_VALUE ? "∞" : String.valueOf(x))
                    .map(s -> String.format("%2s", s))
                    .collect(Collectors.joining(",", "[", "]")));
        }
    }

    static void print(Vertex[][] prev) {
        System.out.println("-------------------------");
        for (Vertex[] row : prev) {
            System.out.println(Arrays.stream(row).map(v -> v == null ? "null" : v.name)
                    .map(s -> String.format("%5s", s))
                    .collect(Collectors.joining(",", "[", "]")));
        }
    }

}

Floyd能否判断负环?

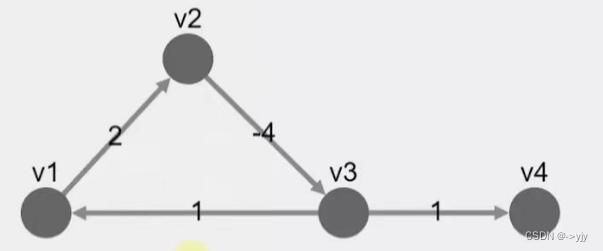
????????v1? ? v2? ? v3? ? v4

?v1? 0? ? ? ?2? ? ?∞? ? ? ?∞

v2? ?∞? ? 0? ? ? ? -4? ? ?∞

v3? 1? ? ?∞? ? ? ? ?0? ? ? ?1

v4??∞? ??∞? ? ? ? ?∞? ? ? ? 0

k=0

????????v1? ? v2? ? v3? ? v4

?v1? 0? ? ? ?2? ? ?∞? ? ? ?∞

v2? ?∞? ? 0? ? ? ? -4? ? ?∞

v3? 1? ? ?3? ? ? ? ?0? ? ? ?1

v4??∞? ??∞? ? ? ? ?∞? ? ? ? 0

k=1

????????v1? ? v2? ? v3? ? v4

?v1? 0? ? ? ?2? ? ?-2? ? ? ?-1

v2? ?∞? ? 0? ? ? ? -4? ? ?∞

v3? 1? ? ?3? ? ? ? ?-1? ? ? 1

v4??∞? ??∞? ? ? ? ?∞? ? ? ? 0

......

负环

如果在 3 层循环结束后，在 dist 数组的对角线处（i==j 处）发现了负数，表示出现了负环