前缀和——OJ题（一）

📘北尘_：个人主页
🌎个人专栏:《Linux操作系统》《经典算法试题 》《C++》 《数据结构与算法》

??走在路上，不忘来时的初心

---

一、除自身以外数组的乘积

1、题目讲解

2、思路讲解

注意题?的要求，不能使?除法，并且要在 O(N) 的时间复杂度内完成该题。那么我们就不能使?暴?的解法，以及求出整个数组的乘积，然后除以单个元素的?法。
继续分析，根据题意，对于每?个位置的最终结果 ret[i] ，它是由两部分组成的：
i. nums[0] * nums[1] * nums[2] * … * nums[i - 1]
ii. nums[i + 1] * nums[i + 2] * … * nums[n - 1]
于是，我们可以利?前缀和的思想，使?两个数组 post 和 suf，分别处理出来两个信息：
i. post 表?：i 位置之前的所有元素，即 [0, i - 1] 区间内所有元素的前缀乘积，
ii. suf 表?： i 位置之后的所有元素，即 [i + 1, n - 1] 区间内所有元素的后缀乘积然后再处理最终结果。

3、代码实现

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
    int n=nums.size();
    vector<int> dp1(n),dp2(n),ret(n);

    dp1[0]=1,dp2[n-1]=1;
    for(int i=1;i<n;i++)
        dp1[i]=dp1[i-1]*nums[i-1];

    for(int i=n-2;i>=0;i--)
        dp2[i]=dp2[i+1]*nums[i+1];

    for(int i=0;i<n;i++)
        ret[i]=dp1[i]*dp2[i];

     return ret;      
    }
};

---

二、寻找数组的中心下标

1、题目讲解

2、思路讲解

从中?下标的定义可知，除中?下标的元素外，该元素左边的「前缀和」等于该元素右边的「后缀和」。
? 因此，我们可以先预处理出来两个数组，?个表?前缀和，另?个表?后缀和。
? 然后，我们可以??个 for 循环枚举可能的中?下标，判断每?个位置的「前缀和」以及「后缀和」，如果?者相等，就返回当前下标。

3、代码实现

class Solution {
public:
    int pivotIndex(vector<int>& nums) {
        int n=nums.size();
        vector<int> dp1(n);
        vector<int> dp2(n);

        dp1[0]=0,dp2[n-1]=0;

        for(int i=1;i<n;i++)
            dp1[i]=dp1[i-1]+nums[i-1];

        for(int i=n-2;i>=0;i--)
           dp2[i]=dp2[i+1]+nums[i+1];

        int m=-1;
        for(int i=0;i<n;i++)
        {
            if(dp1[i]==dp2[i])
            {
                m=i;
                break;
            }
        }
        return m;
    }
};

---

三、【模板】二维前缀和

1、题目讲解

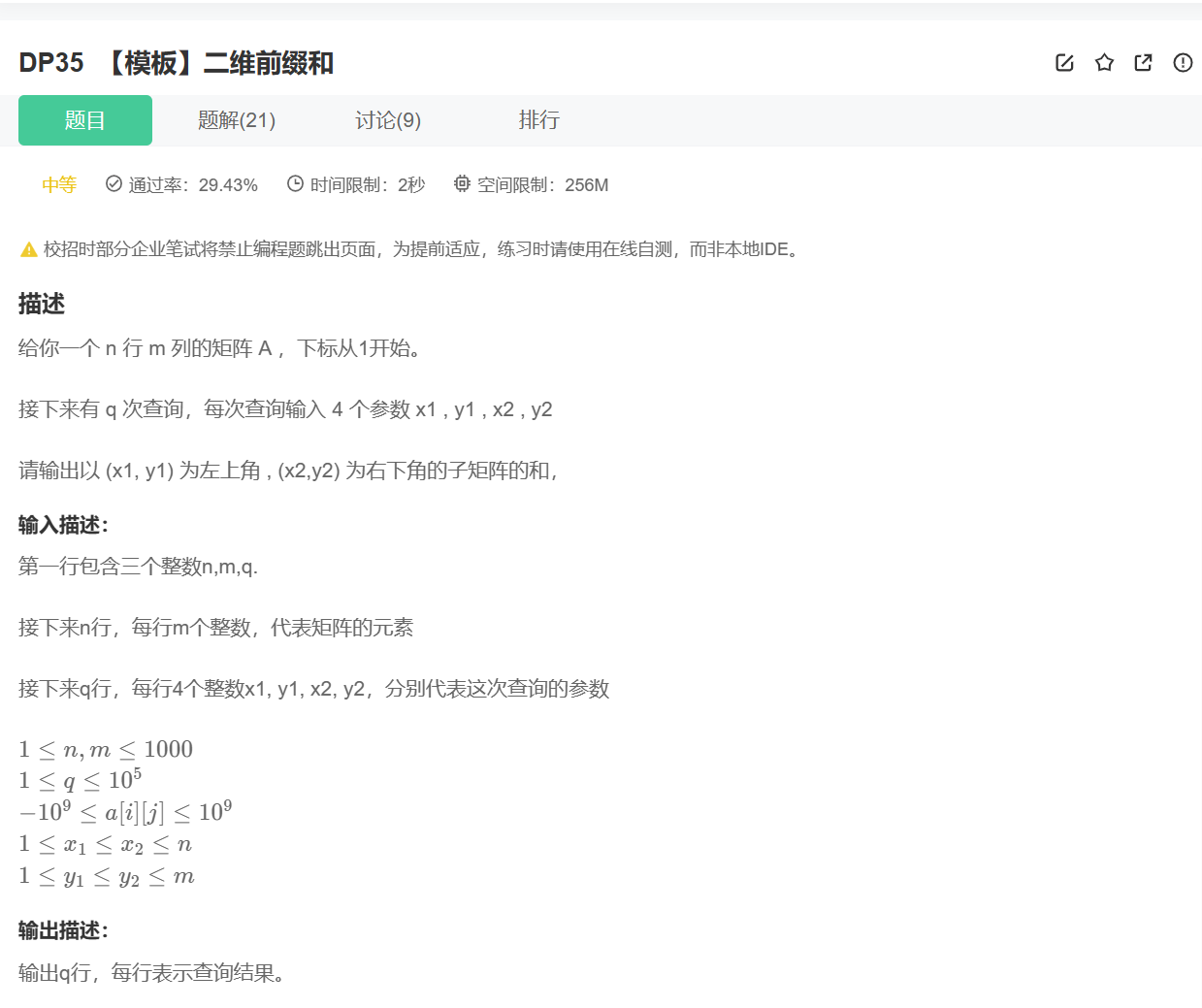
2、思路讲解

类?于?维数组的形式，如果我们能处理出来从 [0, 0] 位置到 [i, j] 位置这?区域内所有元素的累加和，就可以在 O(1) 的时间内，搞定矩阵内任意区域内所有元素的累加和。因此我们接下来仅需完成两步即可：
? 第?步：搞出来前缀和矩阵
这?就要?到?维数组??的拓展知识，我们要在矩阵的最上?和最左边添加上??和?列0，这样我们就可以省去?常多的边界条件的处理（同学们可以??尝试直接搞出来前缀和矩阵，边界条件的处理会让你崩溃的）。处理后的矩阵就像这样：

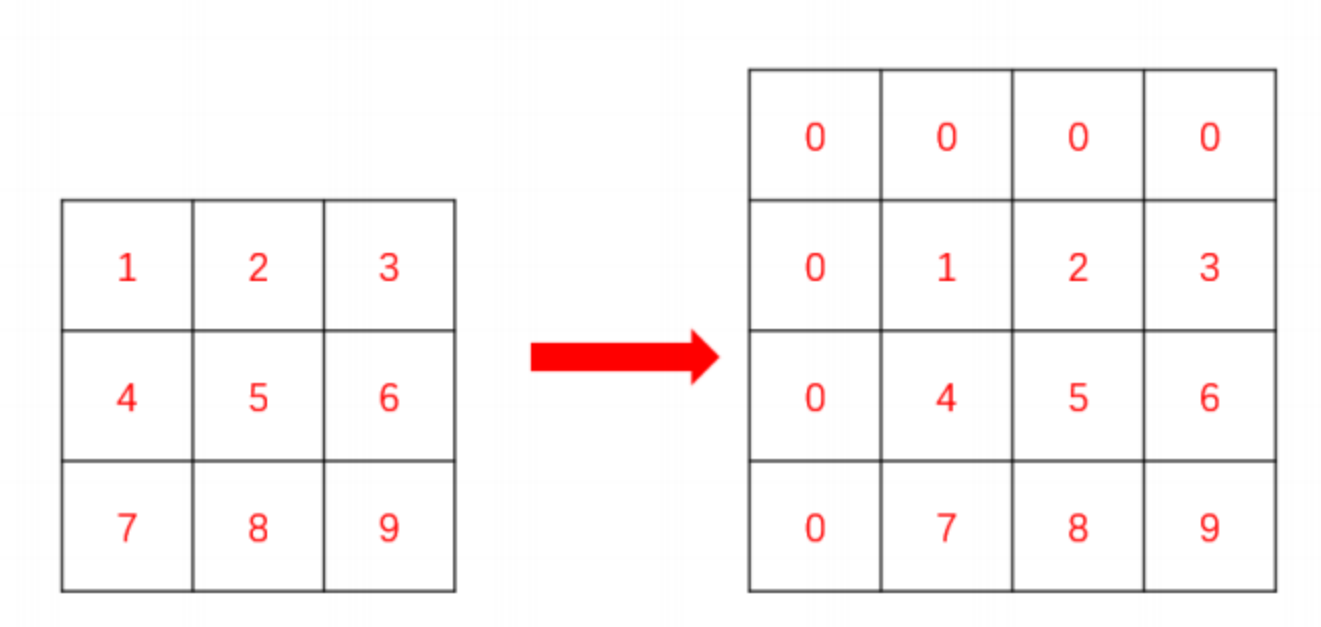
这样，我们填写前缀和矩阵数组的时候，下标直接从 1 开始，能?胆使? i - 1 , j - 1 位置的值。
注意 dp 表与原数组 matrix 内的元素的映射关系：
i. 从 dp 表到 matrix 矩阵，横纵坐标减?；
ii. 从 matrix 矩阵到 dp 表，横纵坐标加?。
前缀和矩阵中 sum[i][j] 的含义，以及如何递推?维前缀和?程
a. sum[i][j] 的含义：
sum[i][j] 表?，从 [0, 0] 位置到 [i, j] 位置这段区域内，所有元素的累加和。对应下图的红?区域：

a. 递推?程：
其实这个递推?程?常像我们?学做过求图形?积的题，我们可以将 [0, 0] 位置到 [i,j]
位置这段区域分解成下?的部分：

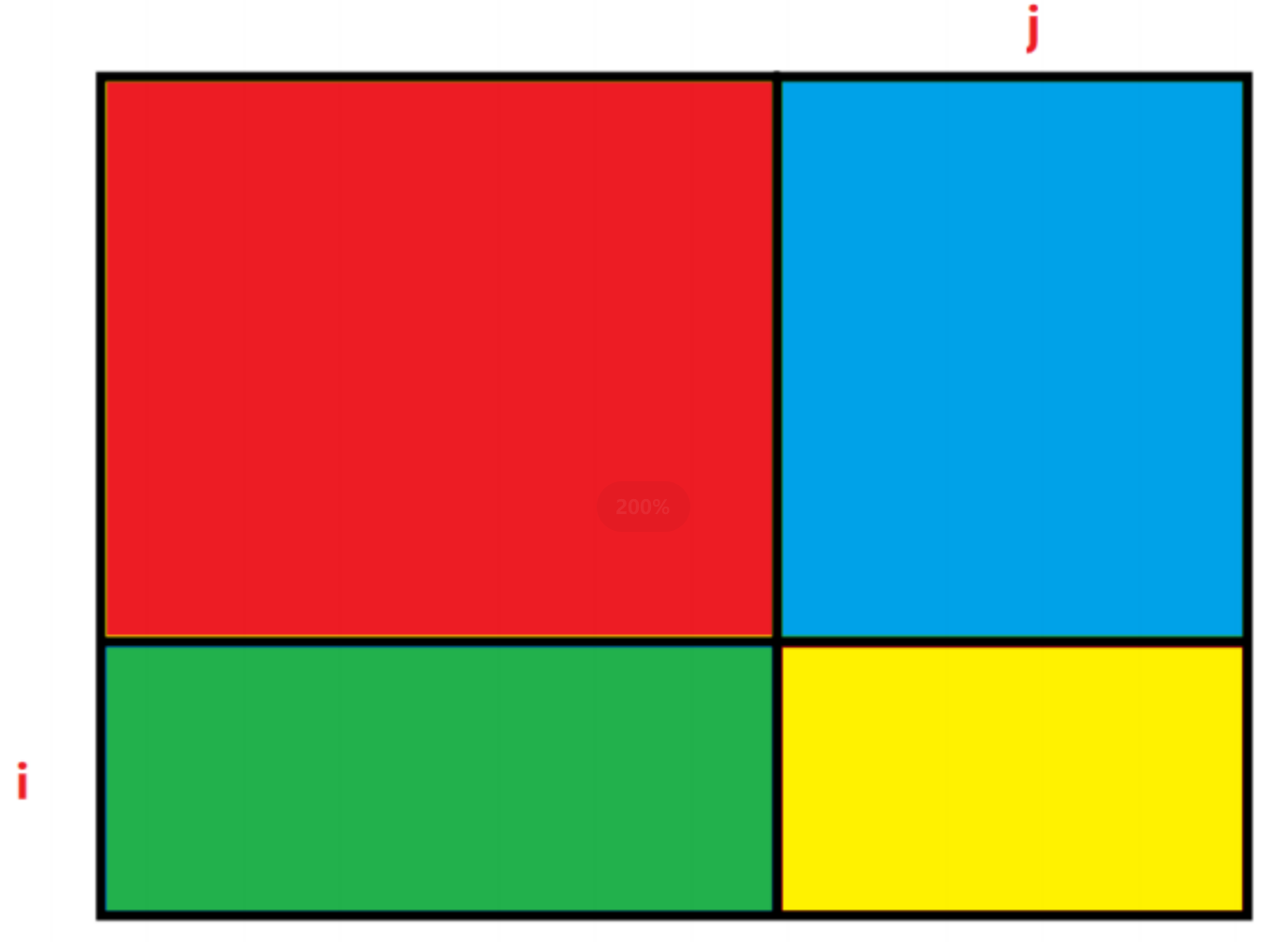
sum[i][j] = 红 + 蓝 + 绿 + ?，分析?下这四块区域：
i. ??部分最简单，它就是数组中的 matrix[i - 1][j - 1] （注意坐标的映射关系）
ii. 单独的蓝不好求，因为它不是我们定义的状态表?中的区域，同理，单独的绿是；
iii. 但是如果是红 + 蓝，正好是我们 dp 数组中 sum[i - 1][j] 的值，美滋滋；
iv. 同理，如果是红 + 绿，正好是我们 dp 数组中 sum[i][j - 1] 的值；
v. 如果把上?求的三个值加起来，那就是? + 红 + 蓝 + 红 + 绿，发现多算了?部分红的?积，因此再单独减去红的?积即可；
vi. 红的?积正好也是符合 dp 数组的定义的，即 sum[i - 1][j - 1]
综上所述，我们的递推?程就是：
sum[i][j]=sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1]+matrix[i - 1][j - 1]
? 第?步：使?前缀和矩阵
题?的接?中提供的参数是原始矩阵的下标，为了避免下标映射错误，这?直接先把下标映射成dp 表??对应的下标： row1++, col1++, row2++, col2++
接下来分析如何使?这个前缀和矩阵，如下图（注意这?的 row 和 col 都处理过了，对应的正是 sum 矩阵中的下标）：

对于左上? (row1, col1) 、右下? (row2, col2) 围成的区域，正好是红?的部分。因
此我们要求的就是红?部分的?积，继续分析?个区域：
i. ??，能直接求出来，就是 sum[row1 - 1, col1 - 1] （为什么减?？因为要剔除掉 row 这??和 col 这?列）
ii. 绿?，直接求不好求，但是和??拼起来，正好是 sum 表内 sum[row1 - 1][col2]
的数据；
iii. 同理，蓝?不好求，但是 蓝 + ? = sum[row2][col1 - 1] ；
iv. 再看看整个?积，好求嘛？?常好求，正好是 sum[row2][col2] ；
v. 那么，红?就 = 整个?积 - ? - 绿 - 蓝，但是绿蓝不好求，我们可以这样减：整个?积 -（绿+ ? ）-（蓝 + ?），这样相当于多减去了?个?，再加上即可
综上所述：红 = 整个?积 - （绿 + ?）- （蓝 + ?）+ ?，从?可得红?区域内的元素总和为：sum[row2][col2]-sum[row2][col1 - 1]-sum[row1 - 1][col2]+sum[row1 -
1][col1 - 1]

3、代码实现

#include <iostream>
#include<vector>
using namespace std;

int main() {
    int n,m,q;
    cin>>n>>m>>q;
    vector<vector<int>> arr(n+1,vector<int>(m+1));
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            cin>>arr[i][j]; 

     vector<vector<long long>> dp(n+1,vector<long long>(m+1));
     for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            dp[i][j]=arr[i][j]+dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1];
        }
    }

    for(int i=0;i<q;i++)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl; 
    }
}

---

四、【模板】一维前缀和

1、题目讲解

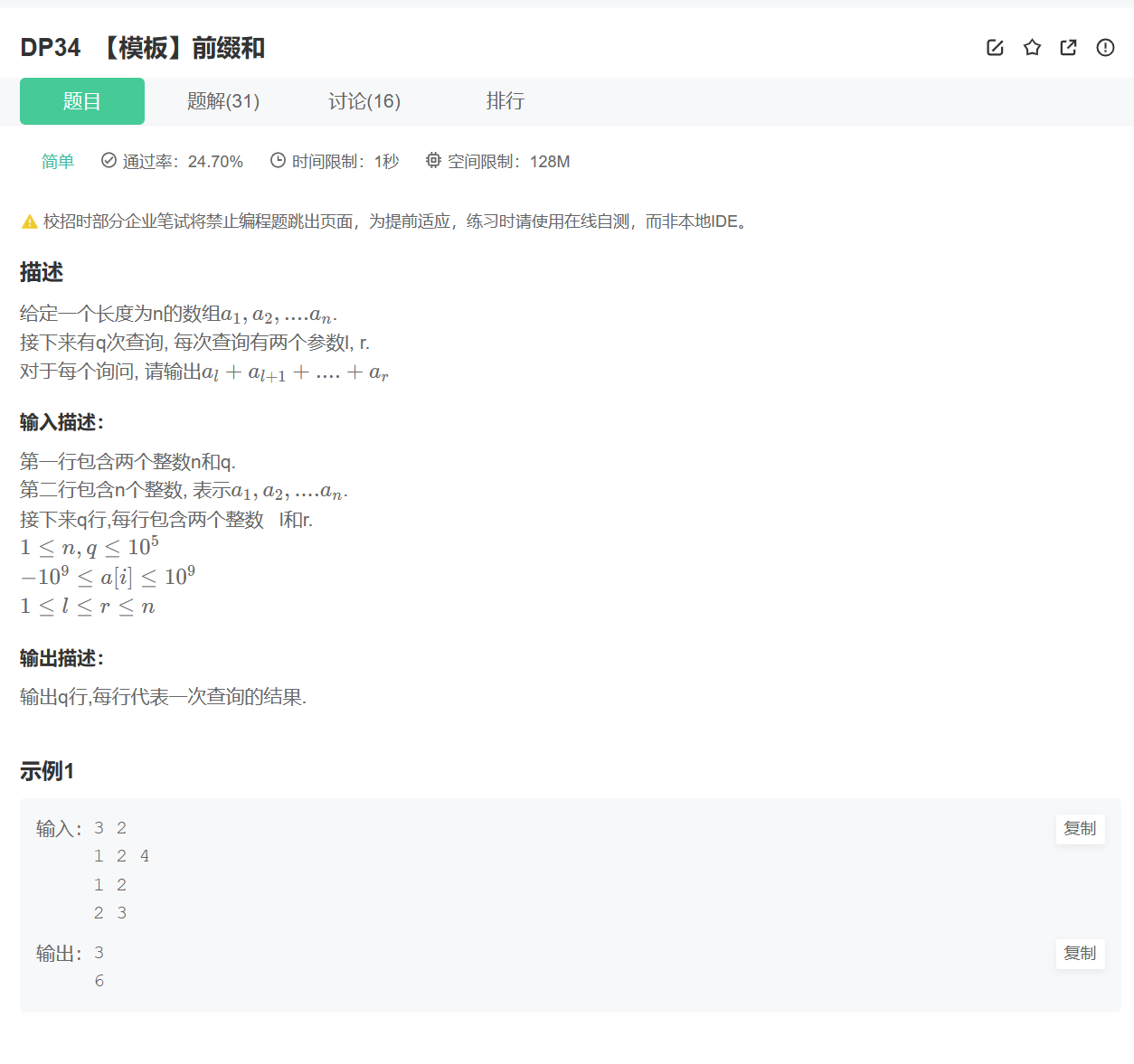
2、思路讲解

a. 先预处理出来?个「前缀和」数组：
? dp[i] 表?： [1, i] 区间内所有元素的和，那么 dp[i - 1] ??存的就是 [1, i - 1] 区间内所有元素的和，那么：可得递推公式： dp[i] = dp[i - 1] + arr[i] ；
b. 使?前缀和数组，「快速」求出「某?个区间内」所有元素的和：
当询问的区间是 [l, r] 时：区间内所有元素的和为： dp[r] - dp[l - 1] 。

3、代码实现

#include <iostream>
#include<vector>
using namespace std;

int main() 
{
    int n,q;
    cin>>n>>q;
    vector<int> v(n+1);
    for(int i=1;i<=n;i++) cin>>v[i];

    vector<long long> dp(n+1);
    for(int i=1;i<=n;i++)  dp[i]=dp[i-1]+v[i];
    
    for(int i=0;i<q;i++)
    {
        int l,r;
        cin>>l>>r;
        cout<<dp[r]-dp[l-1]<<endl;
    }   
}

---