二进制枚举算法
发布时间:2023年12月18日
二进制 :
也就是只有0和1的进制表示 ;
二进制枚举算法
- 一个二进制数 x 可以表示 S 的一个子集,某个二进制位i上为0表示没有选i元素,为1表示选了该元素放入子集,比如13为1101就表示选了0,2,3号元素;
- 对于一个长度为N的序列(也就是包含N个元素)有2^N个子集,因为每个二进制位有两种可能,然后有n个二进制位,所以组合方案数就是2 ^ N 种;
- 用位运算来表示的话,也就是 (1 << N) 种,表示1 左移N位,大小是2 ^ N ,那么枚举也就是
-
for(int i = 0; i < (1<<n); i++) - 然后可以用 x&(1<<i) 来判断当前子集有没有选i元素,&表示与运算,同一为一,不同为0;
- 选取第一、三、四、六、七件物品?1101101(2)=109(10)
- 109&(1<<3)==1?说明?109?对应的子集(选取方案)中包含编号为?3?(第?4?个)元素。
- 109&(1<<4)==0?说明?109?对应的子集(选取方案)中不包含编号为?4?(第?5?个)元素。
输出一个数x的对应子集中所有的元素
for(int i=0;i<n;i++)
if(x&(1<<i))
cout<<i<<endl;枚举所有子集
for(int i = 0; i < (1<<n); i++){
xxxxxx..
}枚举0-2^n-1的每一个状态?
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin >> n;
for(int i = 0; i < (1<<n); i++) //从0~2^n-1个状态 1 左移 n 位
{
printf("%d : ",i) ;
for(int j = 0; j < n; j++)
{
if(i & (1 << j))
{
printf("%d ",j);
}
}
printf("\n");
}
return 0;
}运行效果 :?
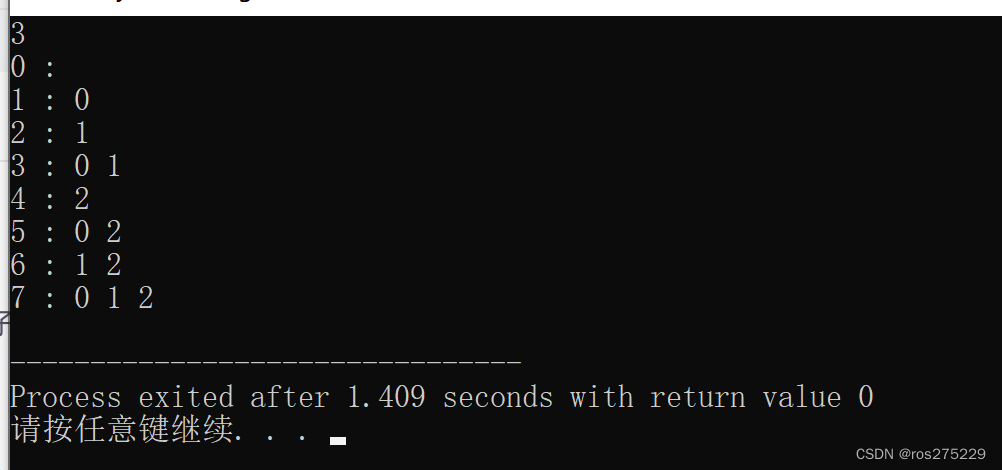
参考 :?
文章来源:https://blog.csdn.net/ros275229/article/details/135070163
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 3000多例-2722-3297-单片机毕业设计项目汇总(合集)电子类毕业设计分享
- AJAX初步与原理
- Linux引导和服务
- 华为配置IPv4静态路由与静态BFD联动示例
- 分支与循环语句总结
- juejin小册git的使用10高级 1:不喜欢 merge 的分叉?用 rebase 吧
- Leetcode 剑指 Offer II 059. 数据流中的第 K 大元素
- redis持久化机制
- 27.移除元素(力扣LeetCode)
- MFC用代码加载一张bmp图片到picture control并适应到控件大小 解决OnInitDialog中调用不显示