73. 矩阵置零

给定一个?m x n?的矩阵，如果一个元素为?0?，则将其所在行和列的所有元素都设为?0?。请使用?原地?算法。

示例 1：

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

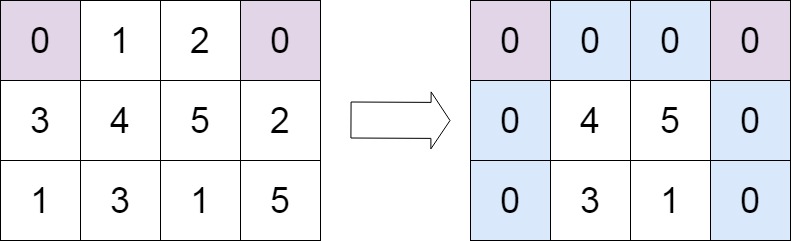
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1

进阶：

• 一个直观的解决方案是使用 ?O(mn)?的额外空间，但这并不是一个好的解决方案。
• 一个简单的改进方案是使用?O(m?+?n)?的额外空间，但这仍然不是最好的解决方案。
• 你能想出一个仅使用常量空间的解决方案吗？

方法1：

    public void setZeroes(int[][] matrix) {
        TreeSet<Integer> rowSet = new TreeSet<>();
        TreeSet<Integer> columnSet = new TreeSet<>();
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                if (matrix[i][j] == 0){
                    rowSet.add(i);
                    columnSet.add(j);
                }
            }
        }
        for (int i = 0; i < matrix.length; i++) {
            if (rowSet.contains(i)){
                Arrays.fill(matrix[i], 0);
            }
        }
        for (int i = 0; i < matrix[0].length; i++) {
            if (columnSet.contains(i)){
                for (int j = 0; j < matrix.length; j++) {
                    matrix[j][i] = 0;
                }
            }
        }
    }

方法2：

    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        // 统计行列是否需要置为0 空间复杂度 O(m+n)
        boolean[] zeroRow = new boolean[m];
        boolean[] zeroCol = new boolean[n];
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(matrix[i][j] == 0){
                    zeroRow[i] = true;
                    zeroCol[j] = true;
                }
            }
        }

        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(zeroRow[i] || zeroCol[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }