红黑树的插入(附代码)
发布时间:2024年01月18日
红黑树
红黑树概念
红黑树是一种二叉搜索树。
每个结点增加一个储存位表示结点的颜色,可以是Red或Black。
其中通过规则对结点着色的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因此保证接近平衡。
红黑树性质
- 每个节点不是红色就是黑色
- 根节点是黑色的
- 如果一个结点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该节点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的
代码部分
结点定义
enum class Color //结点颜色
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
//红黑树结点,默认红色
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_color(Color::RED)
{}
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
Color _color; //结点颜色,红色和黑色
};
插入

下面代码是插入根节点和普通节点部分:
template<class K, class V>
class RBTree
{
private:
typedef RBTreeNode<K, V> Node;
public:
bool Insert(const pair <K, V>& kv)
{
//空树直接申请结点
if (_root == nullptr)
{
_root = new Node(kv);
_root->_color = Color::BLACK; //根结点就置为黑色
return true;
}
//1.找到插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
parent = cur;
cur = cur->_left;
}
}
//2.找到了直接插入
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent; //记得互联
//3.检查是否满足红黑树,若满足直接退出
//不满足,需要调整红黑树
//....
}
检查插入后是否破坏规则
因为插入结点为红色,如果父亲存在且父亲为红色,那么就破坏了规则,需要调整。
//3.检查是否满足红黑树,若满足直接退出
//不满足,需要调整红黑树
while(parent && parent->_color == Color::RED)
{
//...调整
}
调整部分
该部分是爷爷结点的左子树出问题了,右子树出问题与之类似
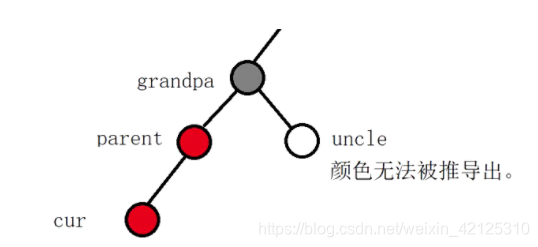
**先给出结论:**看叔叔结点的脸色(颜色)行事。
- 如果叔叔存在且为红。动作:叔父爷变色即可。
- 叔叔存在且为黑/叔叔不存在,根据cur相对于parent的位置,先旋转+染色。
情况1:叔叔存在且为红 直接染色
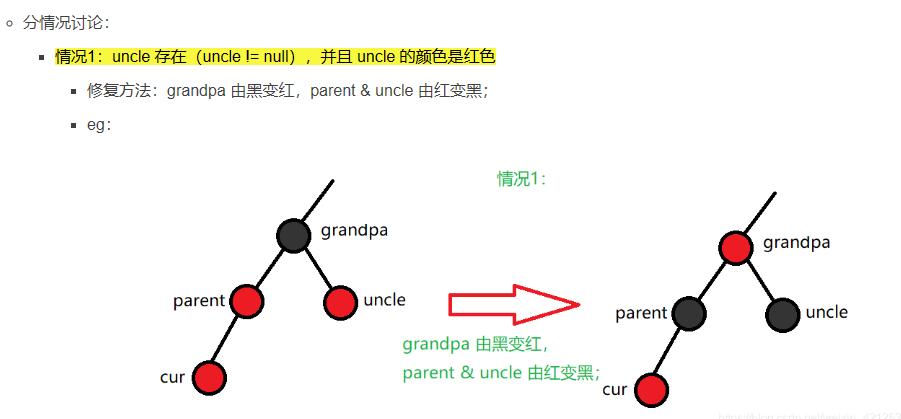
需要注意:如果调整后grandpa的父亲也是红,需要继续向上调整。把grandpa当成新插入的结点即可(cur)。
if (grandfather->_left == parent) //爷爷的左子树出问题了
{
Node* uncle = grandfather->_right;
//情况一: cur 为红,p为红,g为黑, u存在且为红
if (uncle && uncle->_color == Color::RED) // 只需要叔父爷变色即可
{
parent->_color = Color::BLACK;
grandfather->_color = Color::RED;
uncle->_color = Color::BLACK; //子树调整完成
//把爷爷当作新插入结点,继续调整
cur = grandfather;
parent = cur->_parent;
}
情况2:uncle存在且为黑/uncle不存在 。 旋转+变色
-
2.1 单旋+变色(p、g变色)
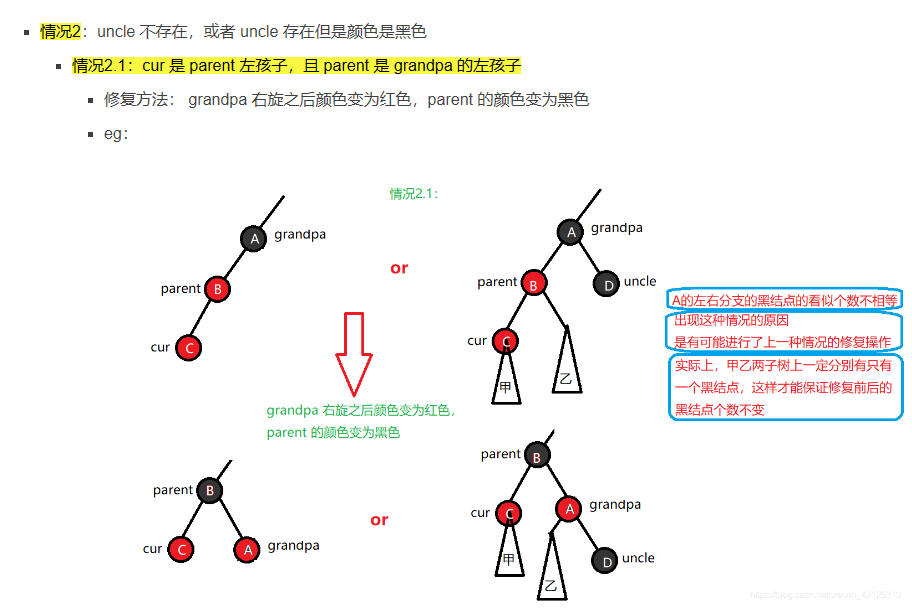
-
2.3 双旋+变色(c、g变色)

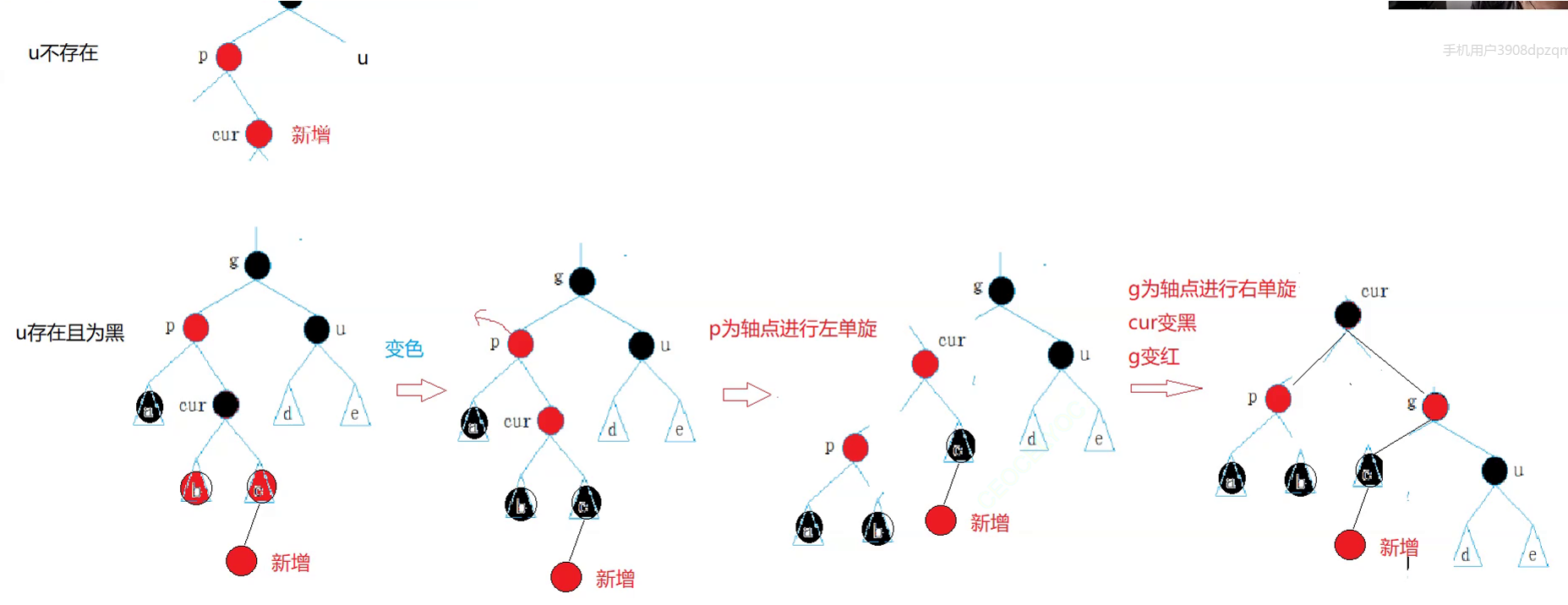
代码部分:
else //2.u存在且为黑 3.u不存在 旋转+变色
{
//2 g
// p u
// c
if (cur == parent->_left) //父亲爷爷变色
{
_RotateR(grandfather); //以g为轴点右单旋
parent->_color = Color::BLACK;
grandfather->_color = Color::RED;
}
else //cur是p的右孩子
{
// g
// p u
// c 叔父爷变色
_RotateL(parent);
_RotateR(grandfather);
grandfather->_color = Color::RED;
cur->_color = Color::BLACK;
}
父亲在爷爷的右边,与上面叙述类似,这里不再赘述
完整代码(赋测测试接口)
enum class Color //结点颜色
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
//红黑树结点,默认红色
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_color(Color::RED)
{}
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
Color _color;
};
template<class K, class V>
class RBTree
{
private:
typedef RBTreeNode<K, V> Node;
public:
bool Insert(const pair <K, V>& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_color = Color::BLACK; //根结点就置为黑色
return true;
}
//1.找到插入位置
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else
{
parent = cur;
cur = cur->_left;
}
}
//2.找到了直接插入
cur = new Node(kv);
if (parent->_kv.first > kv.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
cur->_parent = parent; //记得互联
//3.检查是否满足红黑树,若满足直接退出
//不满足,需要调整红黑树
while(parent && parent->_color == Color::RED)
{
//爷爷结点一定存在,因为parent为红,爷爷结点一定为黑!
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
//情况一: cur 为红,p为红,g为黑, u存在且为红
if (uncle && uncle->_color == Color::RED) // 只需要叔父爷变色即可
{
parent->_color = Color::BLACK;
grandfather->_color = Color::RED;
uncle->_color = Color::BLACK; //子树调整完成
//把爷爷当作新插入结点,继续调整
cur = grandfather;
parent = cur->_parent;
}
else //2.u存在且为黑 3.u不存在 旋转+变色
{
//2 g
// p u
// c
if (cur == parent->_left) //父亲爷爷变色
{
_RotateR(grandfather); //以g为轴点右单旋
parent->_color = Color::BLACK;
grandfather->_color = Color::RED;
}
else //cur是p的右孩子
{
// g
// p u
// c 叔父爷变色
_RotateL(parent);
_RotateR(grandfather);
grandfather->_color = Color::RED;
cur->_color = Color::BLACK;
}
break;
}
}
else //parent = grandfather->_right
{
// g
// u p
// c
Node* uncle = grandfather->_left;
if (uncle && uncle->_color == Color::RED) //情况1 u存在且为红
{
uncle->_color = Color::BLACK;
parent->_color = Color::BLACK;
grandfather->_color = Color::RED;
//继续往上调整
cur = grandfather;
parent = cur->_parent;
}
else //u存在为黑 u不存在
{
// g
// u p
// c
if (cur == parent->_right)
{
//左单旋
_RotateL(grandfather);
parent->_color = Color::BLACK;
grandfather->_color = Color::RED;
}
else
{
// g
// u p
// c
_RotateR(parent);
_RotateL(grandfather);
grandfather->_color = Color::RED;
cur->_color = Color::BLACK;
}
break;
}
}
}
_root->_color = Color::BLACK;
return true;
}
void InOrder()
{
_InOrder(_root);
}
bool IsRBTree()
{
//空树也是红黑树
if (_root == nullptr)
{
return true;
}
if (_root->_color != Color::BLACK)
{
cout << "根节点不是黑色" << endl;
return false;
}
//获取任意一条路径中黑色结点个数
int benchMark = 0;
Node* cur = _root;
while (cur)
{
if (cur->_color == Color::BLACK)
{
benchMark++;
}
cur = cur->_left;
}
return _IsRBTree(_root, 0, benchMark);
}
private:
bool _IsRBTree(Node* root, int blackCount, int benchMark)
{
if (root == nullptr)
{
if (blackCount != benchMark)
{
cout << "黑色结点数量异常" << endl;
return false;
}
return true;
}
if (root->_color == Color::BLACK) //黑节点就计数
{
blackCount++;
}
else //红色结点检查是否满足要求
{
//检查红红
Node* parent = root->_parent;
if (parent && parent->_color == Color::RED)
{
cout << root->_kv.first << "结点不满足红红" << endl;
return false;
}
}
return _IsRBTree(root->_left, blackCount, benchMark) && _IsRBTree(root->_right, blackCount, benchMark);
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_kv.first << " ";
_InOrder(root->_right);
}
void _RotateR(Node* parent)
{
//右单旋,儿子上位变父亲,父亲被挤到右边
Node* pParent = parent->_parent; //爷爷
Node* childL = parent->_left; //左孩子
parent->_left = childL->_right;
if (childL->_right)
{
childL->_right->_parent = parent; //子指向父
}
childL->_right = parent;
parent->_parent = childL; //子指向父
//最后将chldL指向pParent
childL->_parent = pParent;
if (pParent == nullptr) // childL 变成了根
{
_root = childL;
childL->_parent = nullptr;
}
else
{
if (pParent->_left == parent)
{
pParent->_left = childL;
}
else
{
pParent->_right = childL;
}
}
}
//左单旋
void _RotateL(Node* parent)
{
Node* childR = parent->_right; //存右孩子
parent->_right = childR->_left; //右孩子的左孩子互连父亲
if (childR->_left)
{
childR->_left->_parent = parent;
}
childR->_left = parent; //parent和childR互联
Node* pparent = parent->_parent; //暂存爷爷
parent->_parent = childR;
//爷爷和childR互联
childR->_parent = pparent;
if (pparent == nullptr) //爷爷为空,就是根
{
_root = childR;
childR->_parent = nullptr;
}
else
{
if (pparent->_left == parent)
{
pparent->_left = childR;
}
else
{
pparent->_right = childR;
}
}
}
private:
Node* _root=nullptr; //根
};
// 测试接口
void RBTest1()
{
int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
RBTree<int, int> t;
for (auto e : a)
{
t.Insert(pair<int, int>(e, 0));
t.InOrder();
cout << endl;
}
t.InOrder();
}
void RBTest2()
{
//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
RBTree<int, int> t;
for (auto e : a)
{
t.Insert(pair<int, int>(e, 0));
t.InOrder();
cout <<t.IsRBTree()<<endl;
}
t.InOrder();
}
旋转部分介绍,请参考平衡二叉树的插入部分。链接如下:
旋转图例参考文章
文章来源:https://blog.csdn.net/weixin_45153969/article/details/135678964
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Hive09_函数
- 时序数据库InfluxDB、TimeScaleDB简介
- Ubuntu 在更新内核后 Virtual Box 不能为虚拟电脑打开一个新任务
- C语言数据结构-排序
- 图灵日记之java奇妙历险记--数据类型与变量&&运算符
- Matplotlib快速入门,Python通用的绘图工具库上手
- 简易机器学习笔记(十一)opencv 简易使用-人脸识别、分类任务
- 安装光伏,老百姓最担心的5个问题!
- el-table表格中数据过长如何使用省略号
- Kubernetes-持久卷(PV、PVC)