L1-072 刮刮彩票(Java)
发布时间:2024年01月21日
“刮刮彩票”是一款网络游戏里面的一个小游戏。如图所示:
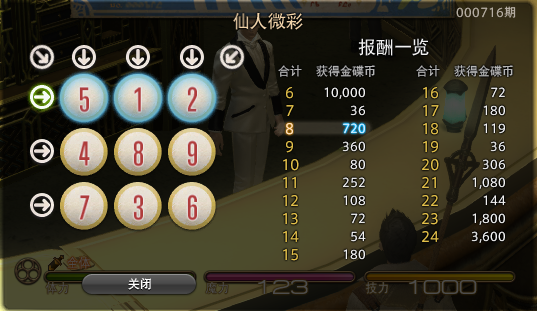
每次游戏玩家会拿到一张彩票,上面会有 9 个数字,分别为数字 1 到数字 9,数字各不重复,并以 3×3 的“九宫格”形式排布在彩票上。
在游戏开始时能看见一个位置上的数字,其他位置上的数字均不可见。你可以选择三个位置的数字刮开,这样玩家就能看见四个位置上的数字了。最后玩家再从 3 横、3 竖、2 斜共 8 个方向中挑选一个方向,方向上三个数字的和可根据下列表格进行兑奖,获得对应数额的金币。
| 数字合计 | 获得金币 | 数字合计 | 获得金币 |
| 6 | 10,000 | 16 | 72 |
| 7 | 36 | 17 | 180 |
| 8 | 720 | 18 | 119 |
| 9 | 360 | 19 | 36 |
| 10 | 80 | 20 | 306 |
| 11 | 252 | 21 | 1,080 |
| 12 | 108 | 22 | 144 |
| 13 | 72 | 23 | 1,800 |
| 14 | 54 | 24 | 3,600 |
| 15 | 180 |
现在请你写出一个模拟程序,模拟玩家的游戏过程。
输入格式:
输入第一部分给出一张合法的彩票,即用 3 行 3 列给出 0 至 9 的数字。0 表示的是这个位置上的数字初始时就能看见了,而不是彩票上的数字为 0。
第二部给出玩家刮开的三个位置,分为三行,每行按格式 x y 给出玩家刮开的位置的行号和列号(题目中定义左上角的位置为第 1 行、第 1 列。)。数据保证玩家不会重复刮开已刮开的数字。
最后一部分给出玩家选择的方向,即一个整数: 1 至 3 表示选择横向的第一行、第二行、第三行,4 至 6 表示纵向的第一列、第二列、第三列,7、8分别表示左上到右下的主对角线和右上到左下的副对角线。
输出格式:
对于每一个刮开的操作,在一行中输出玩家能看到的数字。最后对于选择的方向,在一行中输出玩家获得的金币数量。
输入样例:
1 2 3
4 5 6
7 8 0
1 1
2 2
2 3
7输出样例:
1
5
6
180解题思路
问题分解:
- 通过输入案例结合题目可以得知:玩家可以刮开三个位置的数字,但并不是最终选择,最终选择的方式是挑选一个方向。
- 通过挑选后一个方向上的三个数字相加之后对应表格进行兑奖。
- 输入案例中0代表的是这个位置上的数字初始时就能看见了,之后是要进行替换回原本数字的。
通过问题分解,可以理清楚步骤:
- 设置奖金对照数组,彩票数字数组,标记哪些数字是可见数组
- 替换缺失数字方法,刮开数字时该转为数组索引方法,根据玩家选择方向计算奖金方法
解题过程中遇到的问题
代码
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
private static final int SIZE = 3; // 彩票是3x3的大小
private static final int[] PRIZE = {
10000, 36, 720, 360, 80, 252, 108, 72, 54, 180, 72, 180, 119, 36, 306, 1080, 144, 1800, 3600
}; // 奖金对照表
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int[][] lottery = new int[SIZE][SIZE]; // 彩票数字数组
boolean[] visible = new boolean[10]; // 记录哪些数字是可见的
// 读取彩票数字,并标记可见数字
for (int i = 0; i < SIZE; i++) {
String[] tokens = br.readLine().split(" ");
for (int j = 0; j < SIZE; j++) {
lottery[i][j] = Integer.parseInt(tokens[j]);
if (lottery[i][j] != 0) {
visible[lottery[i][j]] = true;
}
}
}
// 将0替换为缺失的数字
for (int number = 1; number <= SIZE * SIZE; number++) {
if (!visible[number]) {
replaceZero(lottery, number);
break;
}
}
// 刮开数字
for (int i = 0; i < SIZE; i++) {
String[] position = br.readLine().split(" ");
int row = Integer.parseInt(position[0]) - 1;
int col = Integer.parseInt(position[1]) - 1;
System.out.println(lottery[row][col]);
}
// 计算奖金
int direction = Integer.parseInt(br.readLine());
System.out.println(calculatePrize(lottery, direction));
}
// 将0替换为指定的数字
private static void replaceZero(int[][] lottery, int number) {
for (int i = 0; i < lottery.length; i++) {
for (int j = 0; j < lottery[i].length; j++) {
if (lottery[i][j] == 0) {
lottery[i][j] = number;
return;
}
}
}
}
// 根据玩家选择的方向计算奖金
private static int calculatePrize(int[][] lottery, int direction) {
// 根据方向计算行或列的和
int sum = 0;
if (direction >= 1 && direction <= 3) { // 横向
for (int i = 0; i < SIZE; i++) {
sum += lottery[direction - 1][i];
}
} else if (direction >= 4 && direction <= 6) { // 纵向
for (int i = 0; i < SIZE; i++) {
sum += lottery[i][direction - 4];
}
} else if (direction == 7) { // 主对角线
for (int i = 0; i < SIZE; i++) {
sum += lottery[i][i];
}
} else if (direction == 8) { // 副对角线
for (int i = 0; i < SIZE; i++) {
sum += lottery[i][SIZE - 1 - i];
}
}
// 根据总和得出奖金
return PRIZE[sum - 6]; // 数组索引从0开始,和为6的奖金在数组的第0位
}
}
文章来源:https://blog.csdn.net/Gracener/article/details/135729314
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 《学周刊》是什么级别的期刊?是正规期刊吗?能评职称吗?
- 引用阿里图标库,不知道对应的图标是什么,可在本地显示图标ui,再也不要担心刚来不知道公司图标对应的是什么了
- 联想,用PC抢AI船票
- C++类与对象(中)第二篇
- Zookeeper-Zookeeper分布式一致性协议ZAB源码分析(流程图)
- 【JUC进阶】13. InheritableThreadLocal
- iMazing2024免费版iOS移动设备管理软件
- 入行 4 年,跳槽 2 次,我摸透了软件测试这一行!
- AX7A200教程(9): ov5640摄像头输出显示720p视频
- 简述一下组件的生命周期