Python - 深夜数据结构与算法之 Trie

目录

一.引言

二.Tire 树简介

1.基本结构

2.额外信息

3.节点实现

4.存储与查找

5.应用场景

6.基础实现

三.经典算法实战

1.Trie-Tree [208]

2.Word-Search [79]

3.Word-Search-ii [212]

四.总结

---

一.引言

Trie 树即字典树，又称为单词查找树或键树，是一种树形结构，常用于统计，排序和保存大量的字符串，所以经常被搜索引擎系统用于文本词频统计。

◆ 优点 -?利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

◆ 思想?- 其核心思想是空间换时间，通过拆分字符串并存储换取查询的高效率

二.Tire 树简介

1.基本结构

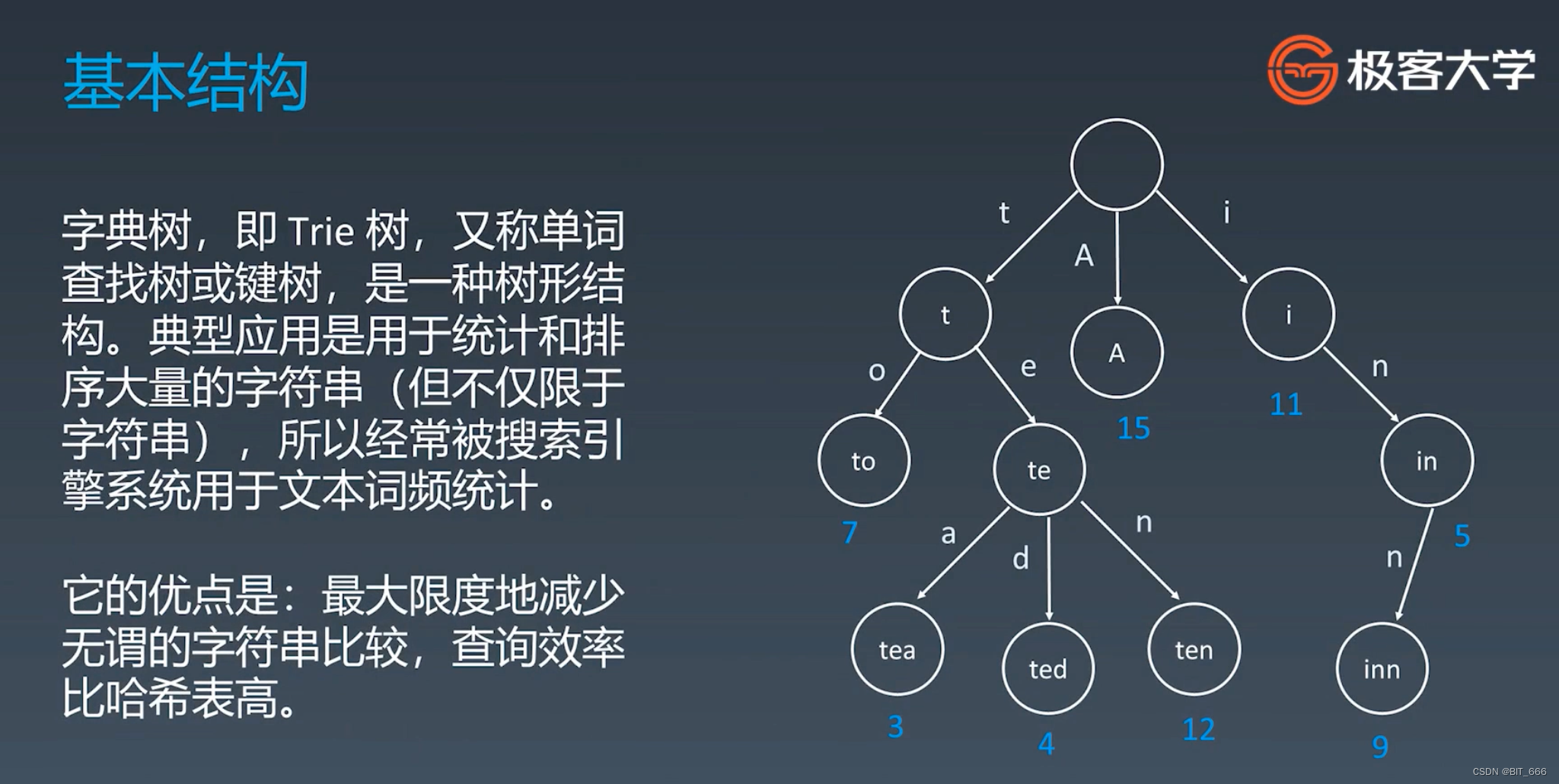
注意这里 Trie 树不是二叉树，而是一颗多叉树，具体分多少叉要根据我们的实际场景来定。例如我们 Trie 树要存储所有英文单词，那理论上每一个父结点 Parent Node 要分 26 个子节点 Child Node，因为英文有 26 个英文字母。Trie 树具备如下基本性质:

◆ 结构本身不存储完整单词，而是存储每个细粒度的拆分项，例如单词搜索则存储字母

◆ 结从根结点到某一结点，将路径上的字符相连，为该结点对应的字符串

◆ 每个结点的所有子结点路径代表的字符都不相同，这里其实代表没有重复字符串结点

2.额外信息

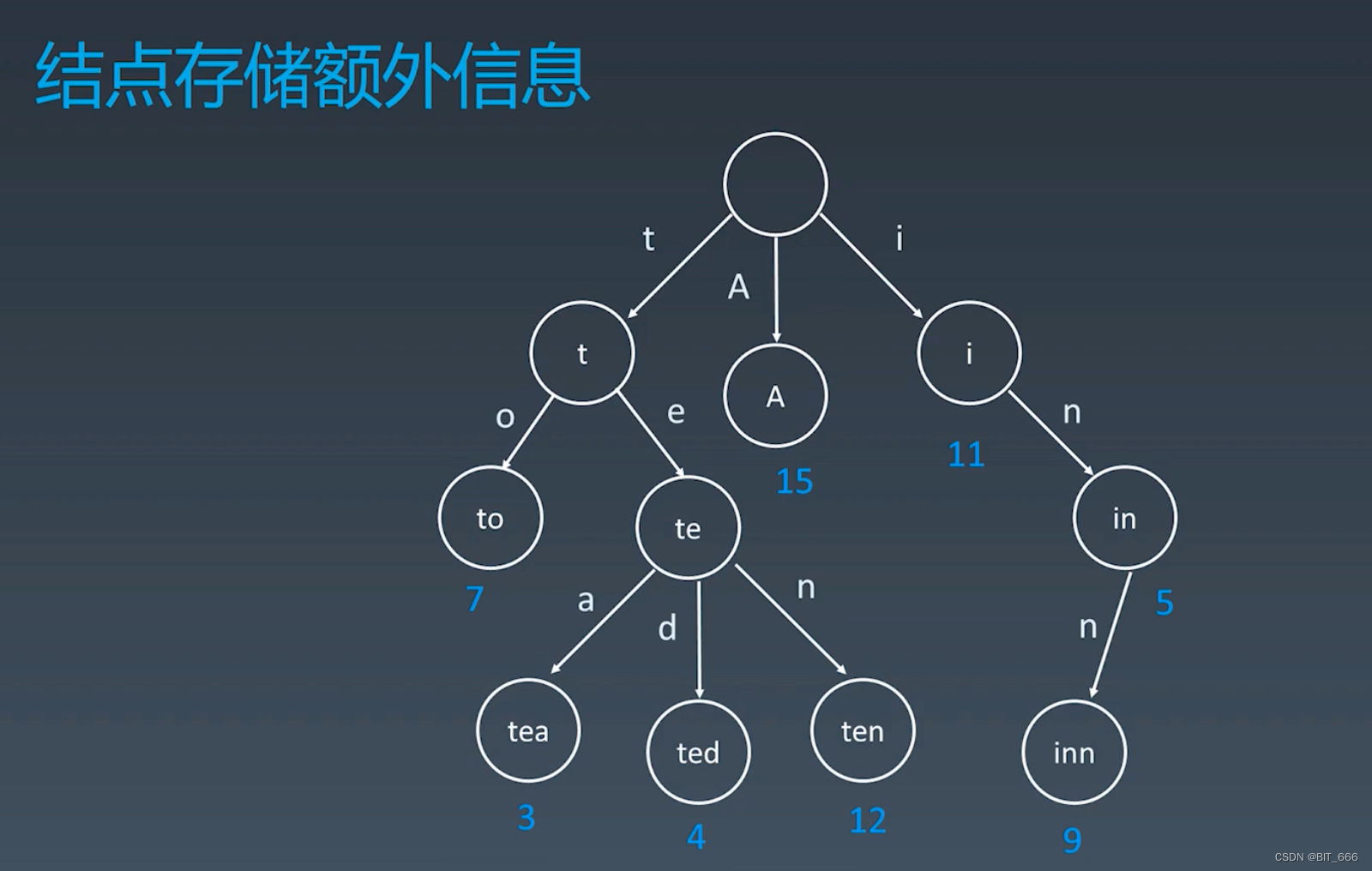
每个 Node 结点除了存储对应的字符外，其还可以具备其自己的属性，最简单的，上面的示例中给出了对应字符串的出现频次，这可以作为搜索推荐的参考依据，如果是代码，其额外信息可以作为一个 Class 存在，内部包含该节点多个属性，例如字符串对应的领域、频率、长度、适用范围等等。?说到词频，也让我们想起来 Word2vec 里用到的霍夫曼树，其在构造编码时也考虑了词频的因素，使得词频高的词可以尽可能快的找到。

3.节点实现

?这里对于每个 Node 而言，结点就不存在 Left 和 Right 的概念了，而是直接对应下一个可能的字符串，选定哪个字符串，就到下一个字符串对应的 Node 上。如果我们认为是简单单词且不区分大小写，我们可以认为每个 Node 最多有 26 个分叉结点，但如果有更多字符或特殊符号的加入，那么多叉树会有更多的分叉。如果一个结点指向 null 代表其没有儿子结点，此时连接其路径上的字符即可得到该结点对应的字符串表示。

4.存储与查找

◆ 存储

假设是上面提到的英文单词查找，且不区分大小写，此时最坏的情况为 26 叉树，每分叉一次，一个结点就多 26 个叉，这样的指数分叉对于存储空间还是有很大的消耗。

◆ 查找

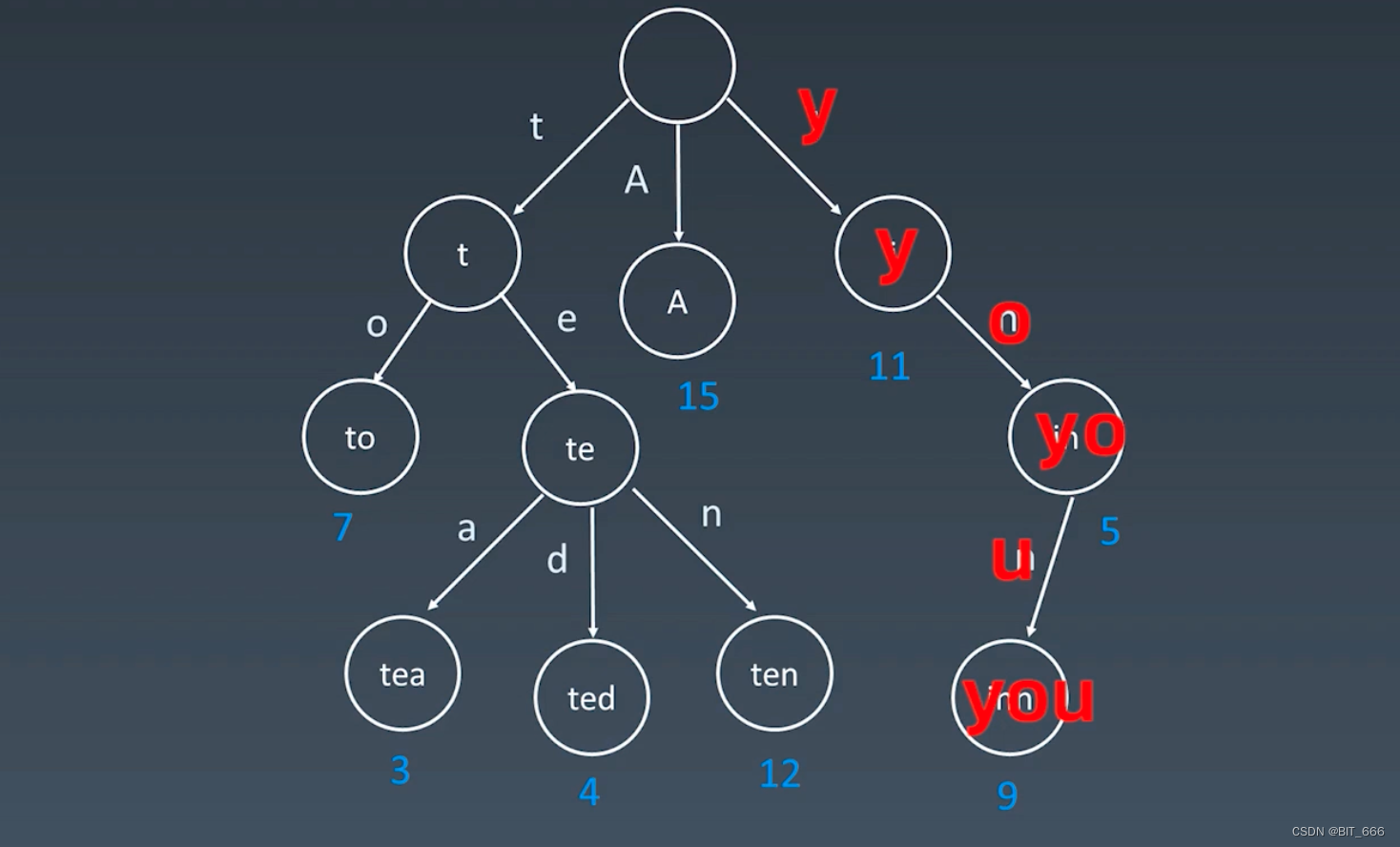
相比于存储的消耗，查找的速度会快很多，因为查找的次数是和单词的字符量匹配的，常见的英文单词字符量在 10 左右，那我们只需要 10 次的常数时间就可以查到，以 you 为例，只需要 3 步就可以找到。但如果是用二分查找等方法，由于整个字典集的数量 n 特别大，即使排好序也是 Log(n) 的查找效率，会比 Trie 树查找次数多很多。这也体现了我们开头说的 Trie 树的核心思想: 空间换时间。其实这个概念不光是 Trie 树，很多算法都会用到这个思想，将时间复杂度降低，空见复杂度提升。

5.应用场景

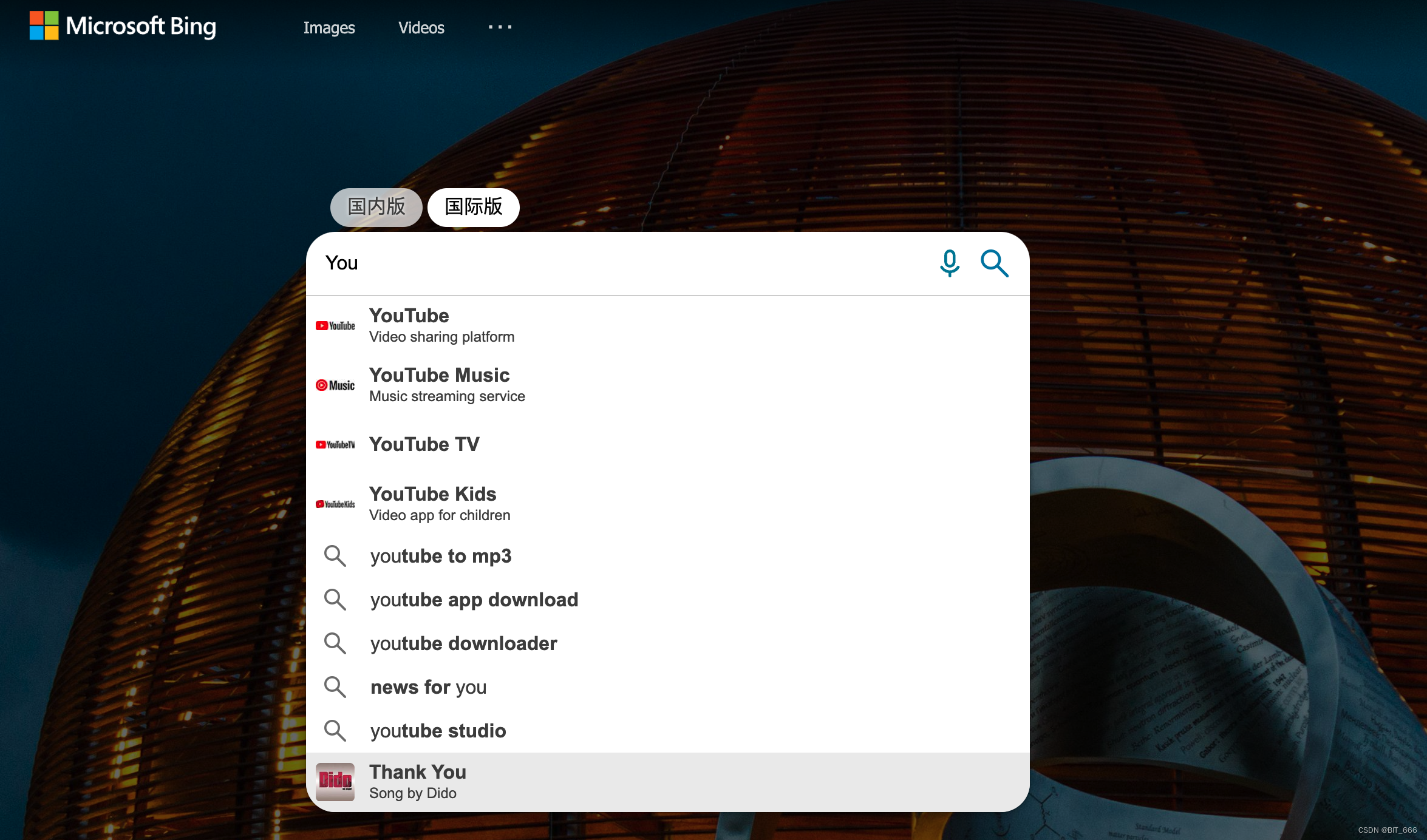
因为 Trie 树公共前缀的使用， 所以它十分适合搜索与输入法拓展等领域，当我们输入了前面的公共前缀，其可以根据词频很容易的给出后面的候选。?实际场景中应用较多的是 Aho-Corasick 算法，其适用于确定性的、完全匹配的字符串搜索场景，它能够高效地检测出预定义的关键词是否在给定文本中出现。针对每一次输入，算法都能找出所有存在的关键词匹配。

6.基础实现

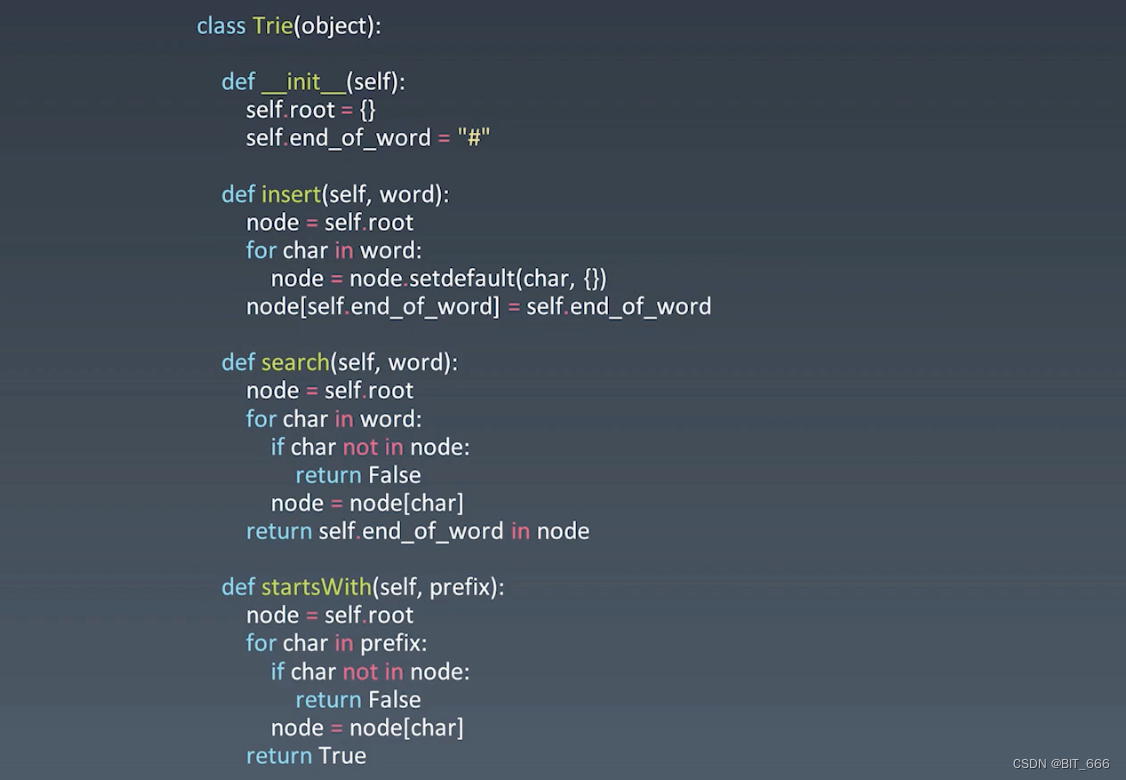
?根据 word 的第一个字母，for 循环判断后面的字母也是否存在。

三.经典算法实战

1.Trie-Tree [208]

实现 Tire 树:?https://leetcode.cn/problems/implement-trie-prefix-tree/

◆ 题目分析

根据上面基础实现的伪代码实现即可。注意题目要求，search 要求完整的包含这个单词，即 is_end = True，startswitg 则不需要，主要这里有一个不同的点。

◆ Trie 实现

class Trie(object):

    def __init__(self):
        self.children = {}  # 存储子节点
        self.is_end = False  # 是否结尾

    def insert(self, word):
        """
        :type word: str
        :rtype: None
        """
        node = self
        for char in word:
            if char not in node.children:
                node.children[char] = Trie()
            node = node.children[char]
        node.is_end = True

    def search(self, word):
        """
        :type word: str
        :rtype: bool
        """
        node = self
        for char in word:
            if char in node.children:
                node = node.children[char]
            else:
                return False
        return node.is_end

    def startsWith(self, prefix):
        """
        :type prefix: str
        :rtype: bool
        """
        node = self
        for char in prefix:
            if char in node.children:
                node = node.children[char]
            else:
                return False
        return True


if __name__ == '__main__':
    tire = Trie()
    tire.insert("hello")
    print(tire.search("hel"))
    print(tire.startsWith("hel"))

2.Word-Search [79]

单词搜索:?https://leetcode.cn/problems/word-search/

◆ 题目分析

通过回朔，遍历 board 中的每个点 i、j，为了防止重复访问，对于访问过的节点要增加 # 标记，这里什么标记都可以，只要能够区分即可，注意在回朔的时候恢复原有状态。

◆ 回朔实现

class Solution(object):
    def exist(self, board, word):
        """
        :type board: List[List[str]]
        :type word: str
        :rtype: bool
        """

        M, N = len(board), len(board[0])

        def dfs(row, col, cur):
            # 匹配到最后一个元素了，找到了
            if cur == "":
                return True

            # 四通遍历
            for r, c in ((row - 1, col), (row + 1, col), (row, col - 1), (row, col + 1)):
                # 边界条件
                if not (0 <= r < M and 0 <= c < N) or board[r][c] == "#":
                    continue

                # Process
                char = board[r][c]
                if char == cur[0]:
                    board[r][c] = "#"
                    if dfs(r, c, cur[1:]):
                        return True
                    else:
                        board[r][c] = char
            return False

        for i in range(M):
            for j in range(N):
                char = board[i][j]
                if char == word[0]:
                    board[i][j] = "#"
                    if dfs(i, j, word[1:]):
                        return True
                    else:
                        board[i][j] = char
        return False

3.Word-Search-ii [212]

单词搜索:?https://leetcode.cn/problems/word-search-ii/description/

◆ 题目分析

基于字典树的思想，我们可以基于 words 里的多个 word 构建 Trie 树，随后 DFS 遍历网格 Board，每次的退出条件是找到 word.is_end = True，不过这里还有一个细节，就是找到一个单词后不立即退出，还需要在判断其后面是否还有扩展。例如寻找 visit 和 visited 两个单词，如果在第一个单词处 return，会少找一个单词。

◆ Trie 树实现?

class TrieNode:
    def __init__(self):
        # 存储 TrieNode 的子节点
        self.children = {}
        # 是否单词结尾
        self.is_end_of_word = False


class Solution(object):

    def findWords(self, board, words):
        """
        :type board: List[List[str]]
        :type words: List[str]
        :rtype: List[str]
        """

        M, N = len(board), len(board[0])
        # 存储搜索到的单词
        result = set()

        def dfs(row, col, node, path):
            # 检查边界条件和当前字符是否为已访问字符（用 "#" 标记）
            if not (0 <= row < M and 0 <= col < N) or board[row][col] == "#":
                return

            char = board[row][col]
            # 如果当前字符不在 TrieNode 的子节点中，直接返回
            if char not in node.children:
                return

            # 获取当前字符对应的子 TrieNode
            child = node.children[char]
            # 如果子 TrieNode 是单词结尾，将单词加入结果集
            if child.is_end_of_word:
                result.add(path + char)
                # 剪枝条件：如果子 TrieNode 没有子节点，直接返回
                if not child.children:
                    return

            # 标记当前字符为已访问字符
            board[row][col] = "#"
            # 遍历上下左右相邻的字符，递归进行 DFS
            for r, c in ((row - 1, col), (row + 1, col), (row, col - 1), (row, col + 1)):
                dfs(r, c, child, path + char)
            # 恢复当前字符，以便其他路径搜索
            board[row][col] = char

        # 创建 Trie 树
        trie = TrieNode()
        for word in words:
            node = trie
            for char in word:
                if char not in node.children:
                    node.children[char] = TrieNode()
                node = node.children[char]
            node.is_end_of_word = True

        # DFS 遍历
        for row in range(M):
            for col in range(N):
                dfs(row, col, trie, "")

        return list(result)

这里构建 Trie 树就是一个循环调用的结构，不断向下拓展 Dict，构建完毕后使用 DFS 进行四通遍历，注意遍历过后的节点进行 # 标记，避免节点重复使用。

四.总结

这里 Trie 树相关的算法题目并不多，我们主要掌握的就是 Trie 树的构建方法以及使用 Trie 树的思想，通过多级 Map 缓存，我们可以在 o(N) 的时间复杂度内找到字符串是否存在。?