秋招复习之栈与队列

---

前言

---

1 栈

「栈 stack」是一种遵循先入后出逻辑的线性数据结构。

我们可以将栈类比为桌面上的一摞盘子，如果想取出底部的盘子，则需要先将上面的盘子依次移走。我们将盘子替换为各种类型的元素（如整数、字符、对象等），就得到了栈这种数据结构。

如图所示，我们把堆叠元素的顶部称为“栈顶”，底部称为“栈底”。将把元素添加到栈顶的操作叫作“入栈”，删除栈顶元素的操作叫作“出栈”。

初始化栈

/* 初始化栈 */
Stack<Integer> stack = new Stack<>();

/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);

/* 访问栈顶元素 */
int peek = stack.peek();

/* 元素出栈 */
int pop = stack.pop();

/* 获取栈的长度 */
int size = stack.size();

/* 判断是否为空 */
boolean isEmpty = stack.isEmpty();

/* 初始化栈 */
stack<int> stack;

/* 元素入栈 */
stack.push(1);
stack.push(3);
stack.push(2);
stack.push(5);
stack.push(4);

/* 访问栈顶元素 */
int top = stack.top();

/* 元素出栈 */
stack.pop(); // 无返回值

/* 获取栈的长度 */
int size = stack.size();

/* 判断是否为空 */
bool empty = stack.empty();

栈的实现

栈遵循先入后出的原则，因此我们只能在栈顶添加或删除元素。然而，数组和链表都可以在任意位置添加和删除元素，因此栈可以视为一种受限制的数组或链表。换句话说，我们可以“屏蔽”数组或链表的部分无关操作，使其对外表现的逻辑符合栈的特性。

基于链表的实现

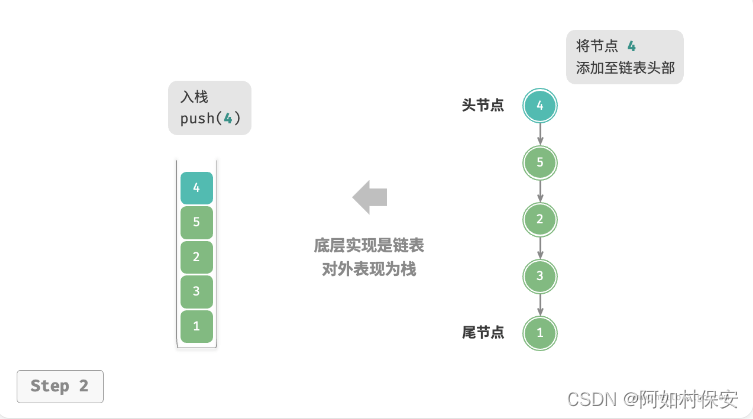
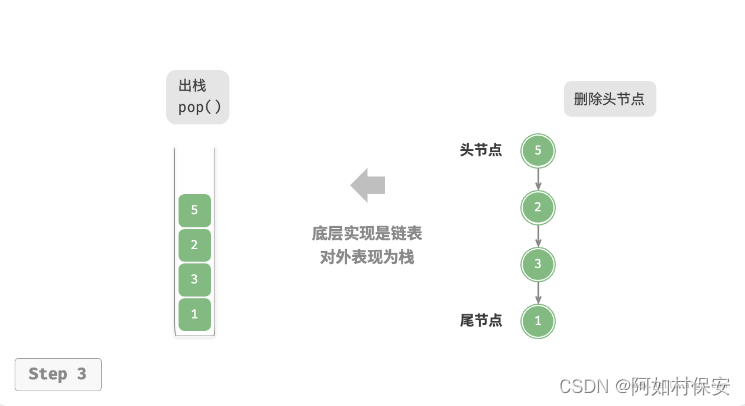
/* 基于链表实现的栈 */
class LinkedListStack {
    private ListNode stackPeek; // 将头节点作为栈顶
    private int stkSize = 0; // 栈的长度

    public LinkedListStack() {
        stackPeek = null;
    }

    /* 获取栈的长度 */
    public int size() {
        return stkSize;
    }

    /* 判断栈是否为空 */
    public boolean isEmpty() {
        return size() == 0;
    }

    /* 入栈 */
    public void push(int num) {
        ListNode node = new ListNode(num);
        node.next = stackPeek;
        stackPeek = node;
        stkSize++;
    }

    /* 出栈 */
    public int pop() {
        int num = peek();
        stackPeek = stackPeek.next;
        stkSize--;
        return num;
    }

    /* 访问栈顶元素 */
    public int peek() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return stackPeek.val;
    }

    /* 将 List 转化为 Array 并返回 */
    public int[] toArray() {
        ListNode node = stackPeek;
        int[] res = new int[size()];
        for (int i = res.length - 1; i >= 0; i--) {
            res[i] = node.val;
            node = node.next;
        }
        return res;
    }
}

/* 基于链表实现的栈 */
class LinkedListStack {
  private:
    ListNode *stackTop; // 将头节点作为栈顶
    int stkSize;        // 栈的长度

  public:
    LinkedListStack() {
        stackTop = nullptr;
        stkSize = 0;
    }

    ~LinkedListStack() {
        // 遍历链表删除节点，释放内存
        freeMemoryLinkedList(stackTop);
    }

    /* 获取栈的长度 */
    int size() {
        return stkSize;
    }

    /* 判断栈是否为空 */
    bool isEmpty() {
        return size() == 0;
    }

    /* 入栈 */
    void push(int num) {
        ListNode *node = new ListNode(num);
        node->next = stackTop;
        stackTop = node;
        stkSize++;
    }

    /* 出栈 */
    int pop() {
        int num = top();
        ListNode *tmp = stackTop;
        stackTop = stackTop->next;
        // 释放内存
        delete tmp;
        stkSize--;
        return num;
    }

    /* 访问栈顶元素 */
    int top() {
        if (isEmpty())
            throw out_of_range("栈为空");
        return stackTop->val;
    }

    /* 将 List 转化为 Array 并返回 */
    vector<int> toVector() {
        ListNode *node = stackTop;
        vector<int> res(size());
        for (int i = res.size() - 1; i >= 0; i--) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};

基于数组的实现

使用数组实现栈时，我们可以将数组的尾部作为栈顶。如图 5-3 所示，入栈与出栈操作分别对应在数组尾部添加元素与删除元素，时间复杂度都为O(1)?。

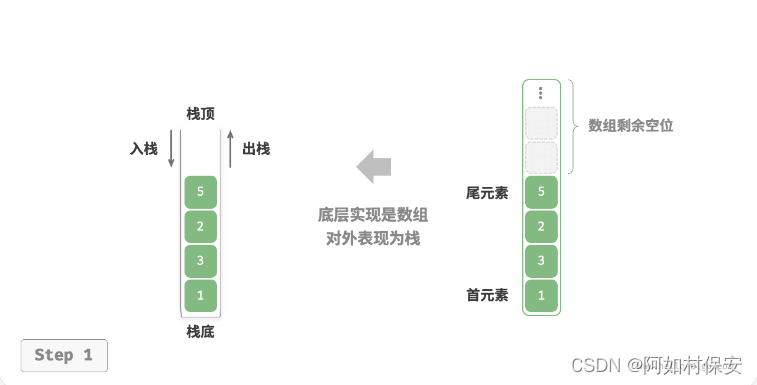
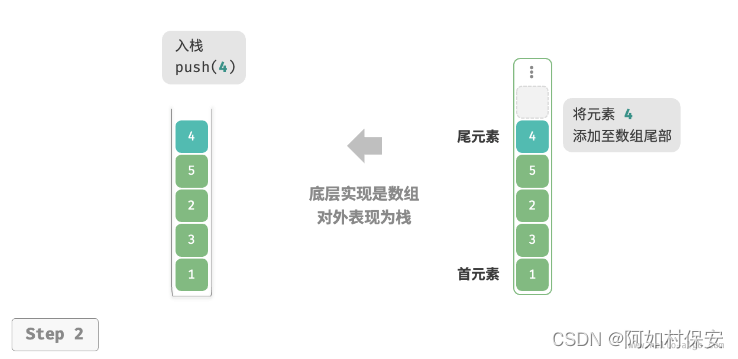
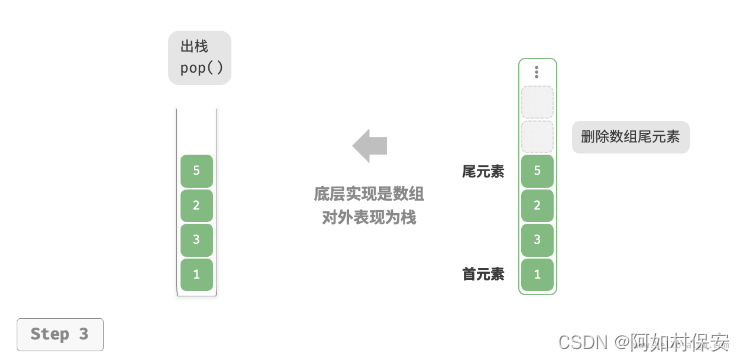
使用动态数组

/* 基于数组实现的栈 */
class ArrayStack {
    private ArrayList<Integer> stack;

    public ArrayStack() {
        // 初始化列表（动态数组）
        stack = new ArrayList<>();
    }

    /* 获取栈的长度 */
    public int size() {
        return stack.size();
    }

    /* 判断栈是否为空 */
    public boolean isEmpty() {
        return size() == 0;
    }

    /* 入栈 */
    public void push(int num) {
        stack.add(num);
    }

    /* 出栈 */
    public int pop() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return stack.remove(size() - 1);
    }

    /* 访问栈顶元素 */
    public int peek() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return stack.get(size() - 1);
    }

    /* 将 List 转化为 Array 并返回 */
    public Object[] toArray() {
        return stack.toArray();
    }
}

/* 基于数组实现的栈 */
class ArrayStack {
  private:
    vector<int> stack;

  public:
    /* 获取栈的长度 */
    int size() {
        return stack.size();
    }

    /* 判断栈是否为空 */
    bool isEmpty() {
        return stack.size() == 0;
    }

    /* 入栈 */
    void push(int num) {
        stack.push_back(num);
    }

    /* 出栈 */
    int pop() {
        int num = top();
        stack.pop_back();
        return num;
    }

    /* 访问栈顶元素 */
    int top() {
        if (isEmpty())
            throw out_of_range("栈为空");
        return stack.back();
    }

    /* 返回 Vector */
    vector<int> toVector() {
        return stack;
    }
};

两种实现对比

支持操作

两种实现都支持栈定义中的各项操作。数组实现额外支持随机访问，但这已超出了栈的定义范畴，因此一般不会用到。

时间效率

在基于数组的实现中，入栈和出栈操作都在预先分配好的连续内存中进行，具有很好的缓存本地性，因此效率较高。然而，如果入栈时超出数组容量，会触发扩容机制，导致该次入栈操作的时间复杂度变为?O(n)?。

在基于链表的实现中，链表的扩容非常灵活，不存在上述数组扩容时效率降低的问题。但是，入栈操作需要初始化节点对象并修改指针，因此效率相对较低。不过，如果入栈元素本身就是节点对象，那么可以省去初始化步骤，从而提高效率。

综上所述，当入栈与出栈操作的元素是基本数据类型时，例如?int?或?double?，我们可以得出以下结论。

• 基于数组实现的栈在触发扩容时效率会降低，但由于扩容是低频操作，因此平均效率更高。
• 基于链表实现的栈可以提供更加稳定的效率表现。

空间效率

在初始化列表时，系统会为列表分配“初始容量”，该容量可能超出实际需求；并且，扩容机制通常是按照特定倍率（例如 2 倍）进行扩容的，扩容后的容量也可能超出实际需求。因此，基于数组实现的栈可能造成一定的空间浪费。

然而，由于链表节点需要额外存储指针，因此链表节点占用的空间相对较大。

综上，我们不能简单地确定哪种实现更加节省内存，需要针对具体情况进行分析。

2?队列

「队列 queue」是一种遵循先入先出规则的线性数据结构。顾名思义，队列模拟了排队现象，即新来的人不断加入队列尾部，而位于队列头部的人逐个离开。

如图所示，我们将队列头部称为“队首”，尾部称为“队尾”，将把元素加入队尾的操作称为“入队”，删除队首元素的操作称为“出队”。

队列的基本操作?

?

/* 初始化队列 */
Queue<Integer> queue = new LinkedList<>();

/* 元素入队 */
queue.offer(1);
queue.offer(3);
queue.offer(2);
queue.offer(5);
queue.offer(4);

/* 访问队首元素 */
int peek = queue.peek();

/* 元素出队 */
int pop = queue.poll();

/* 获取队列的长度 */
int size = queue.size();

/* 判断队列是否为空 */
boolean isEmpty = queue.isEmpty();

/* 初始化队列 */
queue<int> queue;

/* 元素入队 */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);

/* 访问队首元素 */
int front = queue.front();

/* 元素出队 */
queue.pop();

/* 获取队列的长度 */
int size = queue.size();

/* 判断队列是否为空 */
bool empty = queue.empty();

队列的实现

为了实现队列，我们需要一种数据结构，可以在一端添加元素，并在另一端删除元素，链表和数组都符合要求。

基于链表的实现

我们可以将链表的“头节点”和“尾节点”分别视为“队首”和“队尾”，规定队尾仅可添加节点，队首仅可删除节点。

/* 基于链表实现的队列 */
class LinkedListQueue {
    private ListNode front, rear; // 头节点 front ，尾节点 rear
    private int queSize = 0;

    public LinkedListQueue() {
        front = null;
        rear = null;
    }

    /* 获取队列的长度 */
    public int size() {
        return queSize;
    }

    /* 判断队列是否为空 */
    public boolean isEmpty() {
        return size() == 0;
    }

    /* 入队 */
    public void push(int num) {
        // 在尾节点后添加 num
        ListNode node = new ListNode(num);
        // 如果队列为空，则令头、尾节点都指向该节点
        if (front == null) {
            front = node;
            rear = node;
        // 如果队列不为空，则将该节点添加到尾节点后
        } else {
            rear.next = node;
            rear = node;
        }
        queSize++;
    }

    /* 出队 */
    public int pop() {
        int num = peek();
        // 删除头节点
        front = front.next;
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    public int peek() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return front.val;
    }

    /* 将链表转化为 Array 并返回 */
    public int[] toArray() {
        ListNode node = front;
        int[] res = new int[size()];
        for (int i = 0; i < res.length; i++) {
            res[i] = node.val;
            node = node.next;
        }
        return res;
    }
}

/* 基于链表实现的队列 */
class LinkedListQueue {
  private:
    ListNode *front, *rear; // 头节点 front ，尾节点 rear
    int queSize;

  public:
    LinkedListQueue() {
        front = nullptr;
        rear = nullptr;
        queSize = 0;
    }

    ~LinkedListQueue() {
        // 遍历链表删除节点，释放内存
        freeMemoryLinkedList(front);
    }

    /* 获取队列的长度 */
    int size() {
        return queSize;
    }

    /* 判断队列是否为空 */
    bool isEmpty() {
        return queSize == 0;
    }

    /* 入队 */
    void push(int num) {
        // 在尾节点后添加 num
        ListNode *node = new ListNode(num);
        // 如果队列为空，则令头、尾节点都指向该节点
        if (front == nullptr) {
            front = node;
            rear = node;
        }
        // 如果队列不为空，则将该节点添加到尾节点后
        else {
            rear->next = node;
            rear = node;
        }
        queSize++;
    }

    /* 出队 */
    int pop() {
        int num = peek();
        // 删除头节点
        ListNode *tmp = front;
        front = front->next;
        // 释放内存
        delete tmp;
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    int peek() {
        if (size() == 0)
            throw out_of_range("队列为空");
        return front->val;
    }

    /* 将链表转化为 Vector 并返回 */
    vector<int> toVector() {
        ListNode *node = front;
        vector<int> res(size());
        for (int i = 0; i < res.size(); i++) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};

基于数组的实现

在数组中删除首元素的时间复杂度为?O(n)?，这会导致出队操作效率较低。然而，我们可以采用以下巧妙方法来避免这个问题。

我们可以使用一个变量?front?指向队首元素的索引，并维护一个变量?size?用于记录队列长度。定义?rear = front + size?，这个公式计算出的?rear?指向队尾元素之后的下一个位置。

基于此设计，数组中包含元素的有效区间为?[front, rear - 1]，各种操作的实现方法如图。

• 入队操作：将输入元素赋值给?rear?索引处，并将?size?增加 1 。
• 出队操作：只需将?front?增加 1 ，并将?size?减少 1 。

可以看到，入队和出队操作都只需进行一次操作，时间复杂度均为?O(1)?。

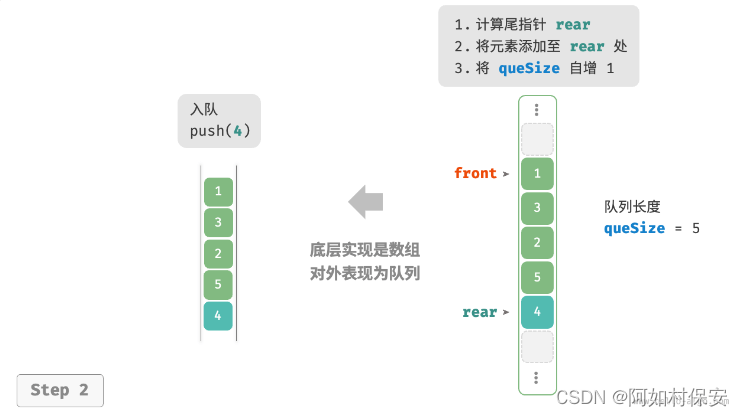
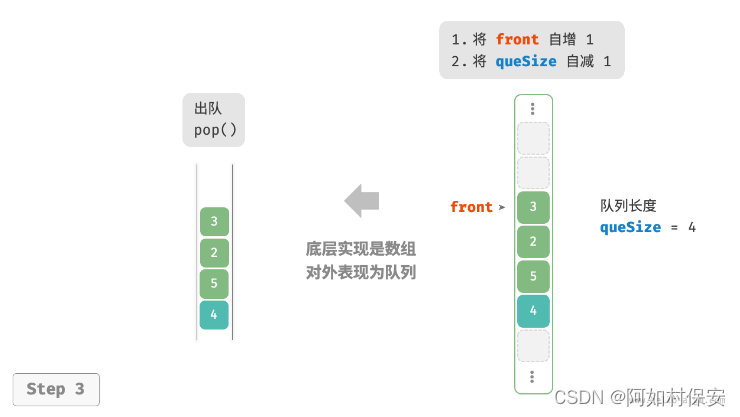
你可能会发现一个问题：在不断进行入队和出队的过程中，front?和?rear?都在向右移动，当它们到达数组尾部时就无法继续移动了。为了解决此问题，我们可以将数组视为首尾相接的“环形数组”。

对于环形数组，我们需要让?front?或?rear?在越过数组尾部时，直接回到数组头部继续遍历。这种周期性规律可以通过“取余操作”来实现，代码如下所示：

/* 基于环形数组实现的队列 */
class ArrayQueue {
    private int[] nums; // 用于存储队列元素的数组
    private int front; // 队首指针，指向队首元素
    private int queSize; // 队列长度

    public ArrayQueue(int capacity) {
        nums = new int[capacity];
        front = queSize = 0;
    }

    /* 获取队列的容量 */
    public int capacity() {
        return nums.length;
    }

    /* 获取队列的长度 */
    public int size() {
        return queSize;
    }

    /* 判断队列是否为空 */
    public boolean isEmpty() {
        return queSize == 0;
    }

    /* 入队 */
    public void push(int num) {
        if (queSize == capacity()) {
            System.out.println("队列已满");
            return;
        }
        // 计算队尾指针，指向队尾索引 + 1
        // 通过取余操作实现 rear 越过数组尾部后回到头部
        int rear = (front + queSize) % capacity();
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }

    /* 出队 */
    public int pop() {
        int num = peek();
        // 队首指针向后移动一位，若越过尾部，则返回到数组头部
        front = (front + 1) % capacity();
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    public int peek() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return nums[front];
    }

    /* 返回数组 */
    public int[] toArray() {
        // 仅转换有效长度范围内的列表元素
        int[] res = new int[queSize];
        for (int i = 0, j = front; i < queSize; i++, j++) {
            res[i] = nums[j % capacity()];
        }
        return res;
    }
}

/* 基于环形数组实现的队列 */
class ArrayQueue {
  private:
    int *nums;       // 用于存储队列元素的数组
    int front;       // 队首指针，指向队首元素
    int queSize;     // 队列长度
    int queCapacity; // 队列容量

  public:
    ArrayQueue(int capacity) {
        // 初始化数组
        nums = new int[capacity];
        queCapacity = capacity;
        front = queSize = 0;
    }

    ~ArrayQueue() {
        delete[] nums;
    }

    /* 获取队列的容量 */
    int capacity() {
        return queCapacity;
    }

    /* 获取队列的长度 */
    int size() {
        return queSize;
    }

    /* 判断队列是否为空 */
    bool isEmpty() {
        return size() == 0;
    }

    /* 入队 */
    void push(int num) {
        if (queSize == queCapacity) {
            cout << "队列已满" << endl;
            return;
        }
        // 计算队尾指针，指向队尾索引 + 1
        // 通过取余操作实现 rear 越过数组尾部后回到头部
        int rear = (front + queSize) % queCapacity;
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }

    /* 出队 */
    int pop() {
        int num = peek();
        // 队首指针向后移动一位，若越过尾部，则返回到数组头部
        front = (front + 1) % queCapacity;
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    int peek() {
        if (isEmpty())
            throw out_of_range("队列为空");
        return nums[front];
    }

    /* 将数组转化为 Vector 并返回 */
    vector<int> toVector() {
        // 仅转换有效长度范围内的列表元素
        vector<int> arr(queSize);
        for (int i = 0, j = front; i < queSize; i++, j++) {
            arr[i] = nums[j % queCapacity];
        }
        return arr;
    }
};

以上实现的队列仍然具有局限性：其长度不可变。然而，这个问题不难解决，我们可以将数组替换为动态数组，从而引入扩容机制。

3?双向队列

在队列中，我们仅能删除头部元素或在尾部添加元素。如图所示，「双向队列 double-ended queue」提供了更高的灵活性，允许在头部和尾部执行元素的添加或删除操作。

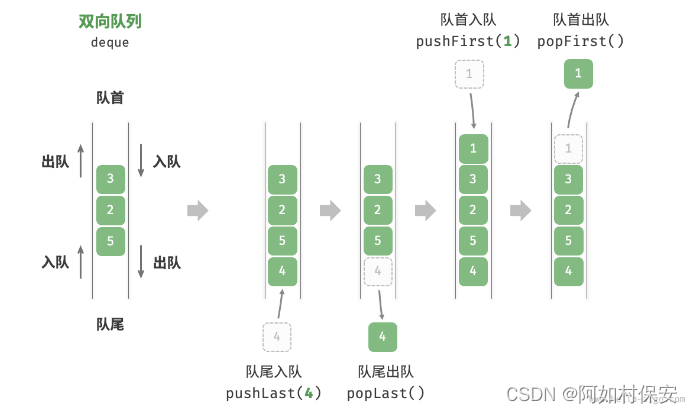双向队列常用操作

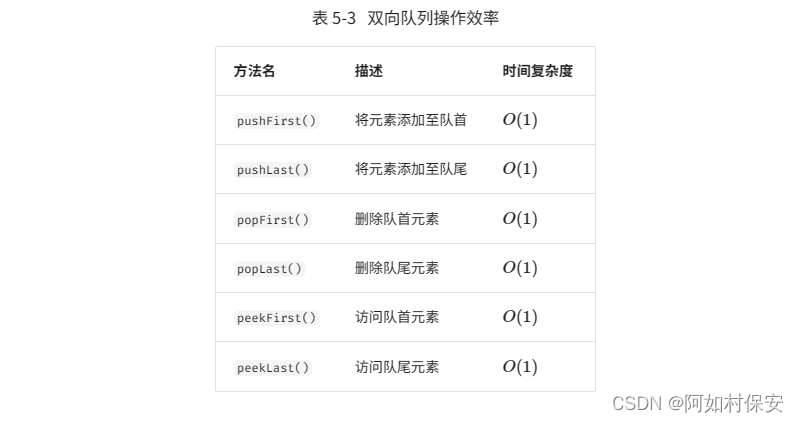
/* 初始化双向队列 */
Deque<Integer> deque = new LinkedList<>();

/* 元素入队 */
deque.offerLast(2);   // 添加至队尾
deque.offerLast(5);
deque.offerLast(4);
deque.offerFirst(3);  // 添加至队首
deque.offerFirst(1);

/* 访问元素 */
int peekFirst = deque.peekFirst();  // 队首元素
int peekLast = deque.peekLast();    // 队尾元素

/* 元素出队 */
int popFirst = deque.pollFirst();  // 队首元素出队
int popLast = deque.pollLast();    // 队尾元素出队

/* 获取双向队列的长度 */
int size = deque.size();

/* 判断双向队列是否为空 */
boolean isEmpty = deque.isEmpty();

/* 初始化双向队列 */
deque<int> deque;

/* 元素入队 */
deque.push_back(2);   // 添加至队尾
deque.push_back(5);
deque.push_back(4);
deque.push_front(3);  // 添加至队首
deque.push_front(1);

/* 访问元素 */
int front = deque.front(); // 队首元素
int back = deque.back();   // 队尾元素

/* 元素出队 */
deque.pop_front();  // 队首元素出队
deque.pop_back();   // 队尾元素出队

/* 获取双向队列的长度 */
int size = deque.size();

/* 判断双向队列是否为空 */
bool empty = deque.empty();

双向队列实现

基于双向链表的实现

使用普通单向链表来实现队列，因为它可以方便地删除头节点（对应出队操作）和在尾节点后添加新节点（对应入队操作）。

对于双向队列而言，头部和尾部都可以执行入队和出队操作。换句话说，双向队列需要实现另一个对称方向的操作。为此，我们采用“双向链表”作为双向队列的底层数据结构。

如图所示，我们将双向链表的头节点和尾节点视为双向队列的队首和队尾，同时实现在两端添加和删除节点的功能。

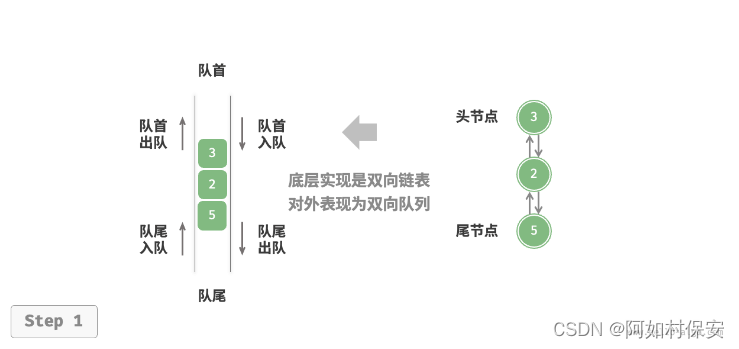
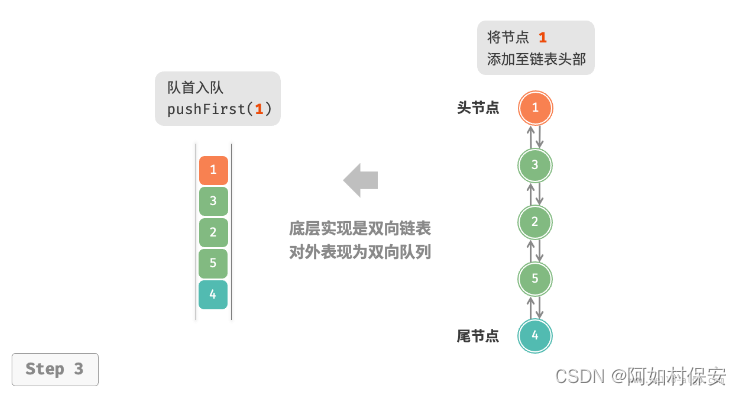
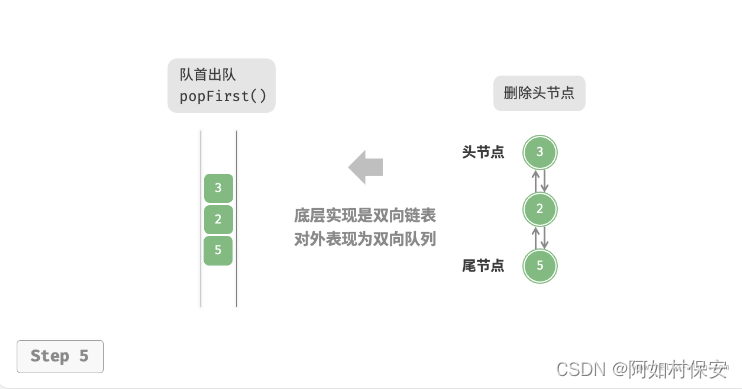
/* 双向链表节点 */
class ListNode {
    int val; // 节点值
    ListNode next; // 后继节点引用
    ListNode prev; // 前驱节点引用

    ListNode(int val) {
        this.val = val;
        prev = next = null;
    }
}

/* 基于双向链表实现的双向队列 */
class LinkedListDeque {
    private ListNode front, rear; // 头节点 front ，尾节点 rear
    private int queSize = 0; // 双向队列的长度

    public LinkedListDeque() {
        front = rear = null;
    }

    /* 获取双向队列的长度 */
    public int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    public boolean isEmpty() {
        return size() == 0;
    }

    /* 入队操作 */
    private void push(int num, boolean isFront) {
        ListNode node = new ListNode(num);
        // 若链表为空，则令 front 和 rear 都指向 node
        if (isEmpty())
            front = rear = node;
        // 队首入队操作
        else if (isFront) {
            // 将 node 添加至链表头部
            front.prev = node;
            node.next = front;
            front = node; // 更新头节点
        // 队尾入队操作
        } else {
            // 将 node 添加至链表尾部
            rear.next = node;
            node.prev = rear;
            rear = node; // 更新尾节点
        }
        queSize++; // 更新队列长度
    }

    /* 队首入队 */
    public void pushFirst(int num) {
        push(num, true);
    }

    /* 队尾入队 */
    public void pushLast(int num) {
        push(num, false);
    }

    /* 出队操作 */
    private int pop(boolean isFront) {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        int val;
        // 队首出队操作
        if (isFront) {
            val = front.val; // 暂存头节点值
            // 删除头节点
            ListNode fNext = front.next;
            if (fNext != null) {
                fNext.prev = null;
                front.next = null;
            }
            front = fNext; // 更新头节点
        // 队尾出队操作
        } else {
            val = rear.val; // 暂存尾节点值
            // 删除尾节点
            ListNode rPrev = rear.prev;
            if (rPrev != null) {
                rPrev.next = null;
                rear.prev = null;
            }
            rear = rPrev; // 更新尾节点
        }
        queSize--; // 更新队列长度
        return val;
    }

    /* 队首出队 */
    public int popFirst() {
        return pop(true);
    }

    /* 队尾出队 */
    public int popLast() {
        return pop(false);
    }

    /* 访问队首元素 */
    public int peekFirst() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return front.val;
    }

    /* 访问队尾元素 */
    public int peekLast() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return rear.val;
    }

    /* 返回数组用于打印 */
    public int[] toArray() {
        ListNode node = front;
        int[] res = new int[size()];
        for (int i = 0; i < res.length; i++) {
            res[i] = node.val;
            node = node.next;
        }
        return res;
    }
}

/* 双向链表节点 */
struct DoublyListNode {
    int val;              // 节点值
    DoublyListNode *next; // 后继节点指针
    DoublyListNode *prev; // 前驱节点指针
    DoublyListNode(int val) : val(val), prev(nullptr), next(nullptr) {
    }
};

/* 基于双向链表实现的双向队列 */
class LinkedListDeque {
  private:
    DoublyListNode *front, *rear; // 头节点 front ，尾节点 rear
    int queSize = 0;              // 双向队列的长度

  public:
    /* 构造方法 */
    LinkedListDeque() : front(nullptr), rear(nullptr) {
    }

    /* 析构方法 */
    ~LinkedListDeque() {
        // 遍历链表删除节点，释放内存
        DoublyListNode *pre, *cur = front;
        while (cur != nullptr) {
            pre = cur;
            cur = cur->next;
            delete pre;
        }
    }

    /* 获取双向队列的长度 */
    int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    bool isEmpty() {
        return size() == 0;
    }

    /* 入队操作 */
    void push(int num, bool isFront) {
        DoublyListNode *node = new DoublyListNode(num);
        // 若链表为空，则令 front 和 rear 都指向 node
        if (isEmpty())
            front = rear = node;
        // 队首入队操作
        else if (isFront) {
            // 将 node 添加至链表头部
            front->prev = node;
            node->next = front;
            front = node; // 更新头节点
        // 队尾入队操作
        } else {
            // 将 node 添加至链表尾部
            rear->next = node;
            node->prev = rear;
            rear = node; // 更新尾节点
        }
        queSize++; // 更新队列长度
    }

    /* 队首入队 */
    void pushFirst(int num) {
        push(num, true);
    }

    /* 队尾入队 */
    void pushLast(int num) {
        push(num, false);
    }

    /* 出队操作 */
    int pop(bool isFront) {
        if (isEmpty())
            throw out_of_range("队列为空");
        int val;
        // 队首出队操作
        if (isFront) {
            val = front->val; // 暂存头节点值
            // 删除头节点
            DoublyListNode *fNext = front->next;
            if (fNext != nullptr) {
                fNext->prev = nullptr;
                front->next = nullptr;
                delete front;
            }
            front = fNext; // 更新头节点
        // 队尾出队操作
        } else {
            val = rear->val; // 暂存尾节点值
            // 删除尾节点
            DoublyListNode *rPrev = rear->prev;
            if (rPrev != nullptr) {
                rPrev->next = nullptr;
                rear->prev = nullptr;
                delete rear;
            }
            rear = rPrev; // 更新尾节点
        }
        queSize--; // 更新队列长度
        return val;
    }

    /* 队首出队 */
    int popFirst() {
        return pop(true);
    }

    /* 队尾出队 */
    int popLast() {
        return pop(false);
    }

    /* 访问队首元素 */
    int peekFirst() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return front->val;
    }

    /* 访问队尾元素 */
    int peekLast() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return rear->val;
    }

    /* 返回数组用于打印 */
    vector<int> toVector() {
        DoublyListNode *node = front;
        vector<int> res(size());
        for (int i = 0; i < res.size(); i++) {
            res[i] = node->val;
            node = node->next;
        }
        return res;
    }
};

基于数组的实现

与基于数组实现队列类似，我们也可以使用环形数组来实现双向队列。

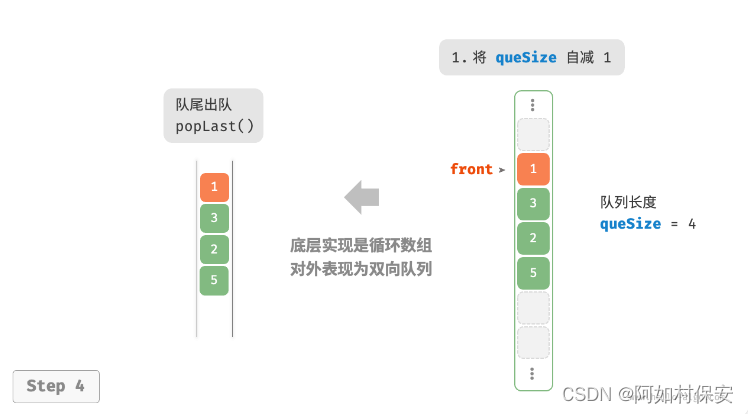
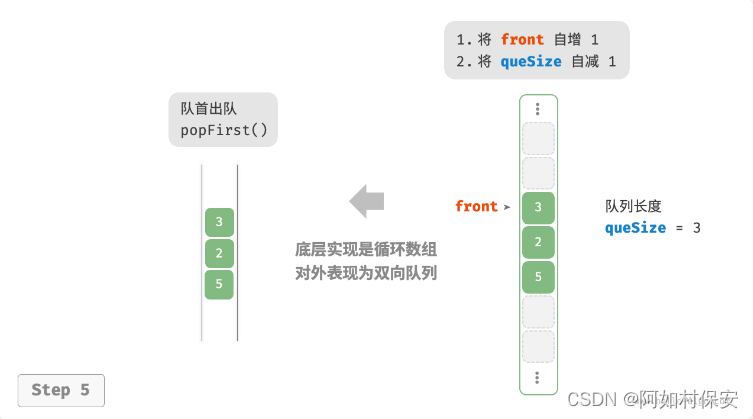
在队列的实现基础上，仅需增加“队首入队”和“队尾出队”的方法：

/* 基于环形数组实现的双向队列 */
class ArrayDeque {
    private int[] nums; // 用于存储双向队列元素的数组
    private int front; // 队首指针，指向队首元素
    private int queSize; // 双向队列长度

    /* 构造方法 */
    public ArrayDeque(int capacity) {
        this.nums = new int[capacity];
        front = queSize = 0;
    }

    /* 获取双向队列的容量 */
    public int capacity() {
        return nums.length;
    }

    /* 获取双向队列的长度 */
    public int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    public boolean isEmpty() {
        return queSize == 0;
    }

    /* 计算环形数组索引 */
    private int index(int i) {
        // 通过取余操作实现数组首尾相连
        // 当 i 越过数组尾部后，回到头部
        // 当 i 越过数组头部后，回到尾部
        return (i + capacity()) % capacity();
    }

    /* 队首入队 */
    public void pushFirst(int num) {
        if (queSize == capacity()) {
            System.out.println("双向队列已满");
            return;
        }
        // 队首指针向左移动一位
        // 通过取余操作实现 front 越过数组头部后回到尾部
        front = index(front - 1);
        // 将 num 添加至队首
        nums[front] = num;
        queSize++;
    }

    /* 队尾入队 */
    public void pushLast(int num) {
        if (queSize == capacity()) {
            System.out.println("双向队列已满");
            return;
        }
        // 计算队尾指针，指向队尾索引 + 1
        int rear = index(front + queSize);
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }

    /* 队首出队 */
    public int popFirst() {
        int num = peekFirst();
        // 队首指针向后移动一位
        front = index(front + 1);
        queSize--;
        return num;
    }

    /* 队尾出队 */
    public int popLast() {
        int num = peekLast();
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    public int peekFirst() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        return nums[front];
    }

    /* 访问队尾元素 */
    public int peekLast() {
        if (isEmpty())
            throw new IndexOutOfBoundsException();
        // 计算尾元素索引
        int last = index(front + queSize - 1);
        return nums[last];
    }

    /* 返回数组用于打印 */
    public int[] toArray() {
        // 仅转换有效长度范围内的列表元素
        int[] res = new int[queSize];
        for (int i = 0, j = front; i < queSize; i++, j++) {
            res[i] = nums[index(j)];
        }
        return res;
    }
}

/* 基于环形数组实现的双向队列 */
class ArrayDeque {
  private:
    vector<int> nums; // 用于存储双向队列元素的数组
    int front;        // 队首指针，指向队首元素
    int queSize;      // 双向队列长度

  public:
    /* 构造方法 */
    ArrayDeque(int capacity) {
        nums.resize(capacity);
        front = queSize = 0;
    }

    /* 获取双向队列的容量 */
    int capacity() {
        return nums.size();
    }

    /* 获取双向队列的长度 */
    int size() {
        return queSize;
    }

    /* 判断双向队列是否为空 */
    bool isEmpty() {
        return queSize == 0;
    }

    /* 计算环形数组索引 */
    int index(int i) {
        // 通过取余操作实现数组首尾相连
        // 当 i 越过数组尾部后，回到头部
        // 当 i 越过数组头部后，回到尾部
        return (i + capacity()) % capacity();
    }

    /* 队首入队 */
    void pushFirst(int num) {
        if (queSize == capacity()) {
            cout << "双向队列已满" << endl;
            return;
        }
        // 队首指针向左移动一位
        // 通过取余操作实现 front 越过数组头部后回到尾部
        front = index(front - 1);
        // 将 num 添加至队首
        nums[front] = num;
        queSize++;
    }

    /* 队尾入队 */
    void pushLast(int num) {
        if (queSize == capacity()) {
            cout << "双向队列已满" << endl;
            return;
        }
        // 计算队尾指针，指向队尾索引 + 1
        int rear = index(front + queSize);
        // 将 num 添加至队尾
        nums[rear] = num;
        queSize++;
    }

    /* 队首出队 */
    int popFirst() {
        int num = peekFirst();
        // 队首指针向后移动一位
        front = index(front + 1);
        queSize--;
        return num;
    }

    /* 队尾出队 */
    int popLast() {
        int num = peekLast();
        queSize--;
        return num;
    }

    /* 访问队首元素 */
    int peekFirst() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        return nums[front];
    }

    /* 访问队尾元素 */
    int peekLast() {
        if (isEmpty())
            throw out_of_range("双向队列为空");
        // 计算尾元素索引
        int last = index(front + queSize - 1);
        return nums[last];
    }

    /* 返回数组用于打印 */
    vector<int> toVector() {
        // 仅转换有效长度范围内的列表元素
        vector<int> res(queSize);
        for (int i = 0, j = front; i < queSize; i++, j++) {
            res[i] = nums[index(j)];
        }
        return res;
    }
};

---

总结

• 栈是一种遵循先入后出原则的数据结构，可通过数组或链表来实现。
• 在时间效率方面，栈的数组实现具有较高的平均效率，但在扩容过程中，单次入栈操作的时间复杂度会劣化至?�(�)?。相比之下，栈的链表实现具有更为稳定的效率表现。
• 在空间效率方面，栈的数组实现可能导致一定程度的空间浪费。但需要注意的是，链表节点所占用的内存空间比数组元素更大。
• 队列是一种遵循先入先出原则的数据结构，同样可以通过数组或链表来实现。在时间效率和空间效率的对比上，队列的结论与前述栈的结论相似。
• 双向队列是一种具有更高自由度的队列，它允许在两端进行元素的添加和删除操作。

啊加油，我可以的！